『括弧・返り点』の研究（Ⅱ）。

（01）
（　）
〔　〕
［　］
｛　｝
〈　〉
を「括弧」とする。
（02）
（　）の中には、「括弧」は無く、
〔　〕の中には、一つ以上の（　）が有り、
［　］の中には、一つ以上の〔　〕が有り、
｛　｝の中には、一つ以上の［　］が有る。
ならば、その時に限って、『括弧』とする。
従って、
（01）（02）により、
（03）
　　（　）
　〔（　）〕
　〔（　）（　）〕
［〔（　）〕（　）］
等は、『括弧』であるが、
〔（　〕）
（〔　）〕
等は、『括弧』ではない。
（04）
「ルール」により、
（Ⅰ）囗の右側が、｛［〔（　と接してゐないならば、「普通に、読む」。
（Ⅱ）囗の右側が、｛［〔（　と接してゐる　ならば、『より内側の「括弧」の中の囗』を「先に読む」。
従って、
（05）
  　　読（漢文）。
　不〔読（漢文）〕。
　有〔読（漢文）者〕。
我不〔必読（漢文）〕。
であれば、
      ３（１２）　　＝漢文を読む。
　４〔３（１２）〕　＝漢文を読まず。
　５〔３（１２）４〕＝漢文を読む者有り。
１６〔２５（３４）〕＝我、必ずしも漢文を読まず。
といふ「順番」で、「括弧」の中を「先に読む」。
従って、
（06）
２囗１
に於いて、
１ を、２ よりも「先に読む」ためには、
２（囗１）
としなければ、ならない。
然るに、
（07）
２（囗１）
に於いて、
　　囗＝３
であれば、
２（３１）
であるため、
１ だけでなく、３ も、２ よりも「先に読む」ことになる。
然るに、
（08）
２１３
に於いて、
１ を、２ よりも「先に読む」ためには、
２（１）３
とすれば、良い。
（09）
２囗１３
に於いて、
１ を、２ よりも「先に読む」ためには、
２（囗１）３
としなければ、ならない。
然るに、
（10）
２（囗１）３
に於いて、
　　囗＝４
であれば、
２（４１）３
であるため、
１ だけでなく、４ も、２ よりも「先に読む」ことになる。
然るに、
（11）
２１４３
に於いて、
１ を、２ よりも「先に読み」、
３ を、４ よりも「先に読む」ためには、
２（１）４（３）
とすれば、良い。
（12）
５囗３（１２）４
に於いて、
３（１２）４ を、５ よりも「先に読む」ためには、
５〔囗３（１２）４〕
としなければ、ならない。
然るに、
（13）
５〔囗３（１２）４〕
に於いて、
　　囗＝６
であれば、
５〔６３（１２）４〕
であるため、
３（１２）４ だけでなく、６ も、５ より「先に読む」ことになる。
然るに、
（14）
５〔３（１２）４〕６
であれば、
１２ を 読んだ後で、３４ を 読み、
３４ を 読んだ後で、５ を 読み、その後で、６ を読む。ことになる。
ｅ.ｇ.
非〔読（漢文）者〕也＝
５〔３（１２）４〕６⇒
〔（１２）３４〕５６＝
〔（漢文）読者〕非也＝
漢文を読む者に非ざるなり。
従って、
（06）～（14）により、
（15）
２（１）３
２（１）４（３）
５〔３（１２）４〕６
ではなく、
２（３１）
２（４１）３
５〔６３（１２）４〕
に於ける、
２＜３＞１（３－１＝２）
２＜４＞１（４－１＝３）
５＜６＞４（６－４＝２）
のやうな、
Ｎ＋１＜Ｎ＋Ａ＞Ｎ（ＮとＡは自然数で、Ａ≧２）
といふ「順番」を含む「順番」は、『括弧』を用ゐて、
Ｎ＜Ｎ＋１＜Ｎ＋Ａ
といふ「順番」に「並び替へ（ソートす）る」ことは、出来ない。
然るに、
（16）
４〔２（１）３〕
４〔２（１）３〕５
５〔２（１）３４〕６
６〔３（１２）４５〕７
７〔１４（２３）５６〕８
１８〔２５（３４）６７〕９
である。
従って、
（17）
例へば、
４２１３
４２１３５
５２１３４６
６３１２４５７
７１４２３５６８
１８２５３４６７９
といふ「順番」は、
Ｎ＋１＜Ｎ＋Ａ＞Ｎ（ＮとＡは自然数で、Ａ≧２）
といふ「順番」を含んでゐない。
（18）
レ
二　一レ
下　上レ
乙　甲レ
地　天レ
一　二　三　四　五　六　七　八　九　十　・　・　・　・　・
上　中　下
甲　乙　丙　丁　戊　己　庚　辛　壬　癸
天　地　人
は、「返り点」である。
然るに、
（19）

従って、
（20）
レ
二　一レ
下　上レ
乙　甲レ
地　天レ
の場合は、
二　一
三　二　一
下　中　上
丙　乙　甲
人　地　天
に「置き換へ」ることが出来る。
従って、
（18）（19）（20）により、
（21）
一　二　三　四　五　六　七　八　九　十　・　・　・　・　・
上　中　下
甲　乙　丙　丁　戊　己　庚　辛　壬　癸
天　地　人
といふ「四種類」を、「返り点」とする。
（22）
（ａ）「下（右）から上（左）へ返る点」であって、「上（左）から下（右）へ返る点」ではない。
（ｂ）天・地点の間には甲・乙点が有り、甲・乙点の間には上・下点（か、一・二点）が有り、上・下点の間には一・二点が有る。
といふ「ルール」に適ふならば、その時に限って、『返り点』であるとする。
然るに、
（23）
① ２　３　１
② ２　３　４　１
に付く「返り点」は、
① 二　三　一
② 二　三　四　一
以外には、有り得ない。
加へて、
（24）
① １　５　２　６　３　４
② ５　１　６　２　７　３
に付く「それ」も、
① 二　三　一
② 二　三　四　一
以外には、有り得ない。
ｃｆ.

従って、
（23）（24）により、
（25）
① ２　３　１
① １　５　２　６　３　４
② ２　３　４　１
② ５　１　６　２　７　３　４
に付く「それ」は、
① 二　三　一
② 二　三　四　一
以外には、有り得ない。
然るに、
（26）
① 二　三　一
② 二　三　四　一
であれば、
① 二 → 三
② 二 → 三 → 四
であるため、「左（上）から右（下）へ返ってゐる」。
然るに、
（22）により、
（27）
（ａ）「左（上）から右（下）へ返ってゐる場合」は『返り点』ではない。
従って、
（26）（27）により、
（28）
① 二　三　一
② 二　三　四　一
といふ「それ」は、『返り点』ではない。
従って、
（25）（28）により、
（29）
① ２　３　１
① １　５　２　６　３　４
② ２　３　４　１
② ５　１　６　２　７　３　４
に付く、
① 二　三　一
② 二　三　四　一
といふ「それ」は、『返り点』ではない。
従って、
（29）により、
（30）
① ２　３　１
① １　５　２　６　３　４
② ２　３　４　１
② ５　１　６　２　７　３　４
といふ「順番」に対しては、『返り点』を付けることは、出来ない。
然るに、
（31）
① ２　３　１
① １　５　２　６　３　４
② ２　３　４　１
② ５　１　６　２　７　３　４
に於いて、
① ２＜３＞１
① ５＜６＞４
② ２＜３＞４＞１
② ５＜６＜７＞４
である。
従って、
（31）により、
（32）
① ２　３　１
① １　５　２　６　３　４
② ２　３　４　１
② ５　１　６　２　７　３　４
といふ「順番」は、
Ｎ＋１＜Ｎ＋Ａ＞Ｎ（ＮとＡは自然数で、Ａ≧２）
といふ「順番」を含む「順番」を含んでゐる。
従って、
（15）（32）により、
（33）
① ２　３　１
① １　５　２　６　３　４
② ２　３　４　１
② ５　１　６　２　７　３　４
といふ「順番」に対して、『括弧』を付けることは、出来ない。
従って、
（30）～（33）により、
（34）
① ２　３　１
① １　５　２　６　３　４
② ２　３　４　１
② ５　１　６　２　７　３　４
のやうに、
① ２＜３＞１
① ５＜６＞４
② ２＜３＞４＞１
② ５＜６＜７＞４
といふ「順番」をふくむ、「順番」に対して、『括弧・返り点』を付けることは、出来ない。
（35）
「１６進数」では足りないため、
Ａ＝１０
Ｂ＝１１
Ｃ＝１２
Ｄ＝１３
Ｅ＝１４
Ｆ＝１５
Ｇ＝１６
Ｈ＝１７
は、「１８進数」である。
然るに、
（36）
例へば、
③ 二　下　丙　人　中　乙　地　上　甲　天　一
③ ２＜５＜８＜Ｃ＞４＜７＜Ｂ＞３＜６＜Ａ＞１
ではなく、
③ Ｂ　８　５　２　１　４　３　７　６　Ａ　９
③ 人　丙　下　二　一　中　上　乙　甲　地　天
であれば、これらの中に、
Ｎ＋１＜Ｎ＋Ａ＞Ｎ（ＮとＡは自然数で、Ａ≧２）
といふ「順番」は、表れない。
従って、
（15）（36）により、
（37）
③ 人　丙　下　二　一　中　上　乙　甲　地　天
といふ『返り点』を伴ふ。
③ Ｂ　８　５　２　１　４　３　７　６　Ａ　９
といふ「順番」は、
③ Ｂ｛８［５〔２（１）４（３）〕７（６）］Ａ（９）｝
といふ『括弧』を用ゐて、
③ ｛［〔（１）２（３）４〕５（６）７］８Ａ（９）｝Ｂ
③ 　　　　１＜２＜３＜４＜５＜６＜７＜８＜９＜Ａ＜Ｂ
といふ「順番」に、「並び替へ（ソートす）る」ことが出来る。
然るに、
（38）
③ Ｈ　１　Ｄ　２　９　５　３　４　８　６　７　Ｃ　Ａ　Ｂ　Ｇ　Ｅ　Ｆ
③ 人　　　丙　　　下　二　　　一　中　　　上　乙　　　甲　地　　　天
③     １＜　　２＜　　　　３＜　　　　６＜　　　　Ａ＜　　　　Ｅ＜
とすれば、これらの中に、
Ｎ＋１＜Ｎ＋Ａ＞Ｎ（ＮとＡは自然数で、Ａ≧２）
といふ「順番」は、表れない。
従って、
（15）（38）により、
（39）
③ 人　　　丙　　　下　二　　　一　中　　　上　乙　　　甲　地　　　天
といふ『返り点』を伴ふ、
③ Ｈ　１　Ｄ　２　９　５　３　４　８　６　７　Ｃ　Ａ　Ｂ　Ｇ　Ｅ　Ｆ
といふ「順番」は、
③ Ｈ｛１　Ｄ［２　９〔５（３　４）８（６　７）〕Ｃ（Ａ　Ｂ）］Ｇ（Ｅ　Ｆ）｝
といふ『括弧』を用ゐて、
③ ｛１　［２　〔（３　４）５（６　７）８〕９（Ａ　Ｂ）Ｃ］Ｄ（Ｅ　Ｆ）Ｇ｝Ｈ
③ 　１＜　２＜　　３＜４＜５＜６＜７＜８＜９＜Ａ＜Ｂ＜Ｃ＜Ｄ＜Ｅ＜Ｆ＜Ｇ＜Ｈ
といふ「順番」に、「並び替へ（ソートす）る」ことが出来る。
然るに、
（40）
例へば、
③ Ｂ　８　５　２　１　４　３　７　６　Ａ　９
③ 人　丙　下　二　一　中　上　乙　甲　地　天
ではなく、
④ Ｂ　８　５　２　３　１　４　７　６　Ａ　９
④ 人　丙　下　二　上　一　中　乙　甲　地　天
であるならば、
④ 　　　　　　　　３　→　４
④ 　　　　　　　　上　→　中
であるため、
（ａ）「左（上）から右（下）へ返ってゐる場合」は『返り点』ではない。
といふことから、
④ Ｂ　８　５　２　３　１　４　７　６　Ａ　９
④ 人　丙　下　二　上　一　中　乙　甲　地　天
は、全体として、『返り点』ではない。
加へて、
（41）
④ 　　　　　　２　３　１
④ 　　　　　　二　上　一
であるため、
（ｂ）上・下点の間には一・二点が有る。
とは言へず、この点に於いても、
④ Ｂ　８　５　２　３　１　４　７　６　Ａ　９
④ 人　丙　下　二　上　一　中　乙　甲　地　天
は、全体として、『返り点』ではない。
然るに、
（42）
③ Ｈ　１　Ｄ　２　９　５　３　４　８　６　７　Ｃ　Ａ　Ｂ　Ｇ　Ｅ　Ｆ
③ 人　　　丙　　　下　二　　　一　中　　　上　乙　　　甲　地　　　天
ではなく、
④ １　Ｄ　Ｈ　２　９　５　３　４　８　６　７　Ｃ　Ａ　Ｂ　Ｇ　Ｅ　Ｆ
④ 　　丙　人　　　下　二　　　一　中　　　上　乙　　　甲　地　　　天
とするならば、
④ 　　丙　人　　　　　　　　　　　　　　　　　乙
であるため、
（ｂ）天・地点の間には甲・乙点が有る。とは言へないため、
④ １　Ｄ　Ｈ　２　９　５　３　４　８　６　７　Ｃ　Ａ　Ｂ　Ｇ　Ｅ　Ｆ
④ 　　丙　人　　　下　二　　　一　中　　　上　乙　　　甲　地　　　天
は、全体として、『返り点』ではない。
然るに、
（43）
④ Ｂ　８　５　２　３　１　４　７　６　Ａ　９
④ 人　丙　下　二　上　一　中　乙　甲　地　天
であれば、
④ 　　　　　　２＜３＞１
であって、
④ １　Ｄ　Ｈ　２　９　５　３　４　８　６　７　Ｃ　Ａ　Ｂ　Ｇ　Ｅ　Ｆ
④ 　　丙　人　　　下　二　　　一　中　　　上　乙　　　甲　地　　　天
であれば、
④ 　　Ｄ＜Ｈ　　　　　　　　　　　　　　　　＞Ｃ
である。
従って、
（15）（43）により、
（44）
④ Ｂ　８　５　２　３　１　４　７　６　Ａ　９
④ １　Ｄ　Ｈ　２　９　５　３　４　８　６　７　Ｃ　Ａ　Ｂ　Ｇ　Ｅ　Ｆ
といふ「順番」は、『括弧』を用ゐて、
④ １＜２＜３＜４＜５＜６＜７＜８＜９＜Ａ＜Ｂ
④ １＜２＜３＜４＜５＜６＜７＜８＜９＜Ａ＜Ｂ＜Ｃ＜Ｄ＜Ｅ＜Ｆ＜Ｇ＜Ｈ
といふ「順番」に、「並び替へ（ソートす）る」ことが出来ない。
従って、
（36）～（44）により、
（45）
③ Ｂ　８　５　２　１　３　４　７　６　Ａ　９
③ Ｈ　１　Ｄ　２　９　５　３　４　８　６　７　Ｃ　Ａ　Ｂ　Ｇ　Ｅ　Ｆ
であれば、
③ Ｂ｛８［５〔２（１）４（３）〕７（６）］Ａ（９）｝
③ 人　丙　下　二　一　中　上　　乙　甲　　地　天
③ Ｈ｛１　Ｄ［２　９〔５（３　４）８（６　７）〕Ｃ（Ａ　Ｂ）］Ｇ（Ｅ　Ｆ）｝
③ 人　　　丙　　　下　二　　　一　中　　　上　　乙　　　甲　　地　　　天
といふ『括弧・返り点』を、付けることが出来、
その一方で、
④ Ｂ　８　５　２　３　１　４　７　６　Ａ　９
④ １　Ｄ　Ｈ　２　９　５　３　４　８　６　７　Ｃ　Ａ　Ｂ　Ｇ　Ｅ　Ｆ
の場合は、『括弧・返り点』を、付けることが出来ない。
従って、
（34）（45）により、
（46）
③ Ｂ　８　５　２　１　３　４　７　６　Ａ　９
③ Ｈ　１　Ｄ　２　９　５　３　４　８　６　７　Ｃ　Ａ　Ｂ　Ｇ　Ｅ　Ｆ
であれば、『括弧・返り点』を、付けることが出来、
その一方で、
① ２　３　１
① １　５　２　６　３　４
② ２　３　４　１
② ５　１　６　２　７　３　４
④ Ｂ　８　５　２　３　１　４　７　６　Ａ　９
④ １　Ｄ　Ｈ　２　９　５　３　４　８　６　７　Ｃ　Ａ　Ｂ　Ｇ　Ｅ　Ｆ
の場合は、『括弧・返り点』を、付けることが出来ない。
然るに、
（47）
① ２　３　１
① １　５　２　６　３　４
② ２　３　４　１
② ５　１　６　２　７　３　４
の場合は、例へば、
① ３　１　２
① １　４　２　３　６　５
② ４　１　３　２
② １　２　７　３　５　４　６　
とすれば、
① ２＜３＞１
① ５＜６＞４
② ２＜３＞４＞１
② ５＜６＜７＞４
といふ「順番」は解消され、その際の『括弧』は、
① ３（１　２）
① １　４（２　３）６（５）
② ４〔１　３（２）〕
② １　２　７〔３　５（４）６〕
であって、『返り点』は、
① 二　一
① 二　一　レ
② 二　一レ
② 二　レ　一
である。
従って、
ｃｆ.

従って、
（20）（21）（45）（46）（47）により、
（48）
（　）
〔　〕
［　］
｛　｝
といふ「括弧」と、
レ
二　一レ
下　上レ
乙　甲レ
地　天レ
一　二　三　四　五　・　・　・　・　・
上　中　下
甲　乙　丙　丁　戊　・　・　・　・　・
天　地　人
といふ「返り点」の間に、「過不足」が生じない限り、
『括弧』　によって表すことが出来る「返読の順番の集合」は、
『返り点』によって表すことが出来る「返読の順番の集合」に等しい。
従って、
（49）
これで「ヲシマイ（Ｑ.Ｅ.Ｄ.）」であると思ふものの、実際にさうか、次の「４０個の順番」等で、確かめることにする。
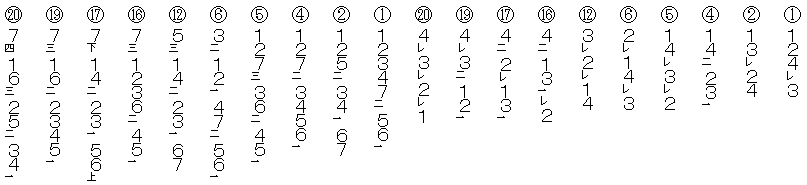
① １２４３
② １３２４
④ １４２３
⑤ １４３２
⑥ ２１４３
⑫ ３２１４
⑯ ４１３２
⑰ ４２１３
⑲ ４３１２
⑳ ４３２１
③ １３４２　＊
⑦ ２３１４　＊
⑧ ２３４１　＊
⑨ ２４１３　＊
⑩ ２４３１　＊
⑪ ３１４２　＊
⑬ ３２４１　＊
⑭ ３４１２　＊
⑮ ３４２１　＊
⑱ ４２３１　＊
① １２３４７５６
② １２５３４６７
④ １２７３４５６
⑤ １２７３６４５
⑥ ３１２４７５６
⑫ ５１４２３６７
⑯ ７１２３６４５
⑰ ７１４２５３６
⑲ ７１６２３４５
⑳ ７１６２５３４
① ２３４７５６１　＊
② ２５３４６７１　＊
④ ２７３４５６１　＊
⑤ ２７３６４５１　＊
⑥ ２４７５６３１　＊
⑫ ４２３６７５１　＊
⑯ ２３６４５７１　＊
⑰ ４２５３６７１　＊
⑲ ６２３４５７１　＊
⑳ ６２５３４７１　＊
（50）
4Ｐ4＝４×３×２×１＝２４個
であるため、
① １２４３
② １３２４
③ １３４２　＊
④ １４２３
⑤ １４３２
⑥ ２１４３
⑦ ２３１４　＊
⑧ ２３４１　＊
⑨ ２４１３　＊
⑩ ２４３１　＊
⑪ ３１４２　＊
⑫ ３２１４
⑬ ３２４１　＊
⑭ ３４１２　＊
⑮ ３４２１　＊
⑯ ４１３２
⑰ ４２１３
⑱ ４２３１　＊
⑲ ４３１２
⑳ ４３２１
の中には、
　 １２３４
　 ２１３４
　 ３１２４
　 ４１２３
が、入っていない。
然るに、
（51）
① １２３４
② ２１３４
③ ３１２４
④ ４１２３
に対する『括弧』は、
① １２３４
② ２（１）３４
③ ３（１２）４
④ ４(１２３）
であって、尚且つ、『返り点』は、
①
② レ
③ 二　一
④ 二　一
である。
ｃｆ.

然るに、
（52）
① １＜２＜３＜４
② ２＞１＜３＜４
③ ３＞１＜２＜４
④ ４＞１＜２＜３
であるため、
① １２３４
② ２１３４
③ ３１２４
④ ４１２３
の場合は、確かに、
Ｎ＋１＜Ｎ＋Ａ＞Ｎ（ＮとＡは自然数で、Ａ≧２）
といふ「順番」を含んでいない。
然るに、
（53）
① １２４３
② １３２４
③ １３４２　＊
④ １４２３
⑤ １４３２
⑥ ２１４３
⑦ ２３１４　＊
⑧ ２３４１　＊
⑨ ２４１３　＊
⑩ ２４３１　＊
⑪ ３１４２　＊
⑫ ３２１４
⑬ ３２４１　＊
⑭ ３４１２　＊
⑮ ３４２１　＊
⑯ ４１３２
⑰ ４２１３
⑱ ４２３１　＊
⑲ ４３１２
⑳ ４３２１
にあって、
① １２４３
② １３２４
④ １４２３
⑤ １４３２
⑥ ２１４３
⑫ ３２１４
⑯ ４１３２
⑰ ４２１３
⑲ ４３１２
⑳ ４３２１
の場合は、
Ｎ＋１＜Ｎ＋Ａ＞Ｎ（ＮとＡは自然数で、Ａ≧２）
といふ「順番」を含んでいない。
然るに、
（54）
① １２４３
② １３２４
④ １４２３
⑤ １４３２
⑥ ２１４３
⑫ ３２１４
⑯ ４１３２
⑰ ４２１３
⑲ ４３１２
⑳ ４３２１
に対する『括弧』は、
① １２４（３）
② １３（２）４
④ １４（２３）
⑤ １４〔３（２）〕
⑥ ２（１）４（３）
⑫ ３〔２（１）〕４
⑯ ４〔１３（２）〕
⑰ ４〔２（１）３〕
⑲ ４〔３（１２）〕
⑳ ４［３〔２（１）〕］
である。
然るに、
（55）
① １２４（３）
② １３（２）４
④ １４（２３）
⑤ １４〔３（２）〕
⑥ ２（１）４（３）
⑫ ３〔２（１）〕４
⑯ ４〔１３（２）〕
⑰ ４〔２（１）３〕
⑲ ４〔３（１２）〕
⑳ ４［３〔２（１）〕］
に対する『返り点』は、
① レ
② レ
④ 二　一
⑤ レ　レ
⑥ レ　レ
⑫ レ　レ
⑯ 二　一レ
⑰ 二　レ　一
⑲ レ　二　一
⑳ レ　レ　レ
である。
ｃｆ.

然るに、
（56）
③ １３４２　＊
⑦ ２３１４　＊
⑧ ２３４１　＊
⑨ ２４１３　＊
⑩ ２４３１　＊
⑪ ３１４２　＊
⑬ ３２４１　＊
⑭ ３４１２　＊
⑮ ３４２１　＊
⑱ ４２３１　＊
といふ「１０個の順番」は、
③ ３＜４＞２　　　＊
⑦ ２＜３＞１　　　＊
⑧ ２＜３＜４＞１　＊
⑨ ２＜４＞１　　　＊
⑩ ２＜４＞３＞１　＊
⑪ ３＜４＞２　　　＊
⑬ ２＜４＞１　　　＊
⑭ ３＜４＞１　　　＊
⑮ ３＜４＞２　　　＊
⑱ ２＜３＞１　　　＊
といふ風に、
Ｎ＋１＜Ｎ＋Ａ＞Ｎ（ＮとＡは自然数で、Ａ≧２）
といふ「順番」を、含んでゐる。
然るに、
（57）
尚且つ、この場合は、
③ １３（４２）　　　＊
⑦ ２（３１）４　　　＊
⑧ ２（３４１）　　　＊
⑨ ２（４１）３　　　＊
⑩ ２（４３１）　　　＊
⑪ ３（１４２）　　　＊
⑬ ３〔２（４１）〕　＊
⑭ ３（４１２）　　　＊
⑮ ３〔４２（１）〕　＊
⑱ ４〔２（３１）〕　＊
といふ『括弧』を用ゐても、
③ １（４２）３　　　＊
⑦ （３１）２４　　　＊
⑧ （３４１）２　　　＊
⑨ （４１）２３　　　＊
⑩ （４３１）２　　　＊
⑪ （１４２）３　　　＊
⑬ 〔（４１）２〕３　＊
⑭ （４１２）３　　　＊
⑮ 〔４（１）２〕３　＊
⑱ 〔（３１）２〕４　＊
といふ「順番」にしか、ならない。
加へて、
（58）
③　 二　三　一　　＊
⑦ 二　三　一　　　＊
⑧ 二　三　四　一　＊
⑨ 二　下　一　上　＊
⑩ 二　四　三　一　＊
⑪ 三　一　四　二　＊
⑬ 三　二　四　一　＊
⑭ 二　三　  一　　＊
⑮ 三　四　二　一　＊
⑱ 下　二　上　一　＊
であるものの、これらは全て、
（ａ）『返り点』は、「下（右）から上（左）へ返る点」であって、「上（左）から下（右）へ返る点」ではない。
（ｂ）天・地点の間には甲・乙点が有り、甲・乙点の間には上・下点（か、一・二点）が有り、上・下点の間には一・二点が有る。
といふ「ルール」に「違反」する。
すなはち、
（59）
⑨ 二　下　一　　　＊
⑱ 二　上　一　　　＊
であれば、却って、
一・二点の間に、上・下点が有り、
③　 二　三　　　　＊
⑦ 二　三　　　　　＊
⑧ 二　三　四　　　＊
⑩ 二　　　三　　　＊
⑪ 三　　　四　　　＊
⑬ 三　　　四　　　＊
⑭ 二　三　 　　 　＊
⑮ 三　四　　　　　＊
であれば、「上（左）から下（右）へ、返ってゐる」。
ｃｆ.

従って、
（53）～（59）により、
（60）
① １２４３
② １３２４
③ １３４２　＊
④ １４２３
⑤ １４３２
⑥ ２１４３
⑦ ２３１４　＊
⑧ ２３４１　＊
⑨ ２４１３　＊
⑩ ２４３１　＊
⑪ ３１４２　＊
⑫ ３２１４
⑬ ３２４１　＊
⑭ ３４１２　＊
⑮ ３４２１　＊
⑯ ４１３２
⑰ ４２１３
⑱ ４２３１　＊
⑲ ４３１２
⑳ ４３２１
といふ「２０個の順番」が与へられた際に、これらの内の「任意の順番」は、
Ｎ＋１＜Ｎ＋Ａ＞Ｎ（ＮとＡは自然数で、Ａ≧２）
といふ「順番＊」を、含んでゐない。ならば、その時に限って、『括弧・返り点』を付けることが、出来る。
然るに、
（61）
① １２４３
に対する、
① １囗２囗４囗３
に於いて、
① 　囗　囗　囗
には、「返り点」は付かない。とするならば、
① １＜囗＞２＜囗＞４＞囗＞３
ではなく、
① １＜囗＜２＜囗＜４＞囗＜３
でなければ、ならない。
（62）
① １＜囗＞２
であれば、例へば、
① １＜３＞２
① １＜４＞２
① １＜５＞２
であるため、
① １＜３＞２
の場合で言へば、
① ３ と ２ の間に、
① 　 レ　が有って、その
①    レ　が、
① ３ に付くことになり、それ故、
① １囗２囗４囗３
に於いて、
① 　囗　囗　囗
には、「返り点」は付かない。とするならば、
① １＜囗＜２＜囗＜４＞囗＜３
でなければ、ならない。
然るに、
（63）
① 　囗　囗　囗
は、「自然数」である。
従って、
（62）（63）により、
（64）
① １＜囗＜２＜囗＜４＞囗＜３
の場合であれば
① １＜２＜３＜４＜７＞５＜６
でなければ、ならない。
従って、
（64）により、
（65）
① １２４３
② １３２４
④ １４２３
⑤ １４３２
⑥ ２１４３
⑫ ３２１４
⑯ ４１３２
⑰ ４２１３
⑲ ４３１２
⑳ ４３２１
に対して、例へば、
① １囗２囗４囗３
② １囗３囗２囗４
④ １囗４囗２囗３
⑤ １囗４囗３囗２
⑥ ２囗１囗４囗３
⑫ ３囗２囗１囗４
⑯ ４囗１囗３囗２
⑰ ４囗２囗１囗３
⑲ ４囗３囗１囗２
⑳ ４囗３囗２囗１
といふ風に、囗を加へたとして、囗には、『返り点』が付かないとすれば、
① １２３４７５６
② １２５３４６７
④ １２７３４５６
⑤ １２７３６４５
⑥ ３１２４７５６
⑫ ５１４２３６７
⑯ ７１２３６４５
⑰ ７１４２３５６
⑲ ７１６２３４５
⑳ ７１６２５３４
といふ「順番」になる。
然るに、
（66）
① １２４３
① １２３４７５６
であれば、
① １　２　４　３
① １　３　７　６
① １２３４７５６
である。
従って、
（67）
① １　２　４　３
といふ「順番」が、
Ｎ＋１＜Ｎ＋Ａ＞Ｎ（ＮとＡは自然数で、Ａ≧２）
といふ「順番＊」を、含んでゐないのであれば、
① １２３４７５６
といふ「順番」も、
Ｎ＋１＜Ｎ＋Ａ＞Ｎ（ＮとＡは自然数で、Ａ≧２）
といふ「順番＊」を、含んでゐない。
従って、
（53）（65）（66）（67）により、
（68）
① １２４３
② １３２４
④ １４２３
⑤ １４３２
⑥ ２１４３
⑫ ３２１４
⑯ ４１３２
⑰ ４２１３
⑲ ４３１２
⑳ ４３２１
が、さうであるやうに、
① １２３４７５６
② １２５３４６７
④ １２７３４５６
⑤ １２７３６４５
⑥ ３１２４７５６
⑫ ５１４２３６７
⑯ ７１２３６４５
⑰ ７１４２３５６
⑲ ７１６２３４５
⑳ ７１６２５３４
といふ「順番」は、
Ｎ＋１＜Ｎ＋Ａ＞Ｎ（ＮとＡは自然数で、Ａ≧２）
といふ「順番」を含んでゐない。
従って、
（15）（16）（54）（68）により、
（69）
① １２３４７５６
② １２５３４６７
④ １２７３４５６
⑤ １２７３６４５
⑥ ３１２４７５６
⑫ ５１４２３６７
⑯ ７１２３６４５
⑰ ７１４２３５６
⑲ ７１６２３４５
⑳ ７１６２５３４
に対する『括弧』も、
① １　２　４　３
② １　３　２　４
④ １　４　２　３
⑤ １　４　３　２
⑥ ２　１　４　３
⑫ ３　２　１　４
⑯ ４　１　３　２
⑰ ４　２　１　３
⑲ ４　３　１　２
⑳ ４　３　２　１
と同じく、
① １２３４７（５６）
② １２５（３４）６７
④ １２７（３４５６）
⑤ １２７〔３６（４５）〕
⑥ ３（１２）４７（５６）
⑫ ５〔１４（２３）〕６７
⑯ ７〔１２３６（４５）〕
⑰ ７〔１４（２３）５６〕
⑲ ７〔１６（２３４５）〕
⑳ ７［１６〔２５（３４）〕］
である。
然るに、
（70）
① １２３４７５６
② １２５３４６７
④ １２７３４５６
⑤ １２７３６４５
⑥ ３１２４７５６
⑫ ５１４２３６７
⑯ ７１２３６４５
⑰ ７１４２３５６
⑲ ７１６２３４５
⑳ ７１６２５３４
に対して、「レ点」は、付かないため、『返り点』は、
① レ
② レ
④ 二　一
⑤ レ　レ
⑥ レ　レ
⑫ レ　レ
⑯ 二　一レ
⑰ 二　レ　一
⑲ レ　二　一
⑳ レ　レ　レ
ではなく、
① 二　一
② 二　一
④ 二　一
⑤ 三　二　一
⑥ 二　一　二　一
⑫ 三　二　一
⑯ 三　二　一
⑰ 下　二　一　上
⑲ 三　二　一
⑳ 四　三　二　一
である。
ｃｆ.

従って、
（60）（69）（70）により、
（71）
① １２４３
② １３２４
④ １４２３
⑤ １４３２
⑥ ２１４３
⑫ ３２１４
⑯ ４１３２
⑰ ４２１３
⑲ ４３１２
⑳ ４３２１
③ １３４２　＊
⑦ ２３１４　＊
⑧ ２３４１　＊
⑨ ２４１３　＊
⑩ ２４３１　＊
⑪ ３１４２　＊
⑬ ３２４１　＊
⑭ ３４１２　＊
⑮ ３４２１　＊
⑱ ４２３１　＊
といふ「２０個の順番」に対して、
① １２３４７５６
② １２５３４６７
④ １２７３４５６
⑤ １２７３６４５
⑥ ３１２４７５６
⑫ ５１４２３６７
⑯ ７１２３６４５
⑰ ７１４２３５６
⑲ ７１６２３４５
⑳ ７１６２５３４
といふ「１０個の順番」が加はった、「３０個の順番」が与へられた際に、これらの内の「任意の順番」は、
Ｎ＋１＜Ｎ＋Ａ＞Ｎ（ＮとＡは自然数で、Ａ≧２）
といふ「順番＊」を、含んでゐない。ならば、その時に限って、『括弧・返り点』を付けることが、出来る。
（72）
① １│２３４７５６
② １│２５３４６７
④ １│２７３４５６
⑤ １│２７３６４５
⑥ ３１│２４７５６
⑫ ５１│４２３６７
⑯ ７１│２３６４５
⑰ ７１│４２３５６
⑲ ７１│６２３４５
⑳ ７１│６２５３４
といふ「順番」を、「│の位置で、前後を入れ換へる」と、
① │２３４７５６１
② │２５３４６７１
④ │２７３４５６１
⑤ │２７３６４５１
⑥ │２４７５６３１
⑫ │４２３６７５１
⑯ │２３６４５７１
⑰ │４２３５６７１
⑲ │６２３４５７１
⑳ │６２５３４７１
となって、これらは全て、少なくとも、
① │２＜３＞１
② │２＜５＞１
④ │２＜７＞１
⑤ │２＜７＞１
⑥ │２＜４＞１
⑫ │２＜３＞１
⑯ │２＜３＞１
⑰ │２＜３＞１
⑲ │２＜３＞１
⑳ │２＜５＞１
といふ「順番」を含んでゐる。
従って、
（72）により、
（73）
① ２３４７５６１　＊
② ２５３４６７１　＊
④ ２７３４５６１　＊
⑤ ２７３６４５１　＊
⑥ ２４７５６３１　＊
⑫ ４２３６７５１　＊
⑯ ２３６４５７１　＊
⑰ ４２３５６７１　＊
⑲ ６２３４５７１　＊
⑳ ６２５３４７１　＊
といふ「順番」は、
Ｎ＋１＜Ｎ＋Ａ＞Ｎ（ＮとＡは自然数で、Ａ≧２）
といふ「順番＊」を、含んでゐる。
然るに、
（74）
例へば、
① ２３４７５６１　＊
であれば、
① ２‐３‐４７５‐６１　＊
のやうに、「ハイフン」を用ゐることにする。
従って、
（75）
① ２‐３‐４７５‐６１　＊
② ２５３‐４６‐７１　　＊
④ ２７３‐４‐５‐６１　＊
⑤ ２７３６４‐５１　　　＊
⑥ ２４７５‐６３１　　　＊
⑫ ４２‐３６‐７５１　　＊
⑯ ２‐３６４‐５７１　　＊
⑰ ４２‐３５‐６‐７１　＊
⑲ ６２‐３‐４‐５７１　＊
⑳ ６２５３‐４７１　　　＊
に於ける、
① ２‐３‐４　５‐６
② ３‐４　６‐７
④ ３‐４‐５‐６
⑤ ４‐５
⑥ ５‐６
⑫ ２‐３ ６‐７
⑯ ２‐３ ４‐５
⑰ ２‐３ ５‐６‐７
⑲ ２‐３‐４‐５
⑳ ３‐４
等は、それぞれが、「熟語（ａ word）」でなければならない。
従って、
（75）により、
（76）
例えば、
① ２‐３‐４７５‐６１　＊
であれば、
①「七文字」からなる「四語」である。
ｃｆ.
ＷＯＲＤ は、　「四文字」からなる「一語」。
漢字 は、通常、「一文字」からなる「一語」。
従って、
（75）（76）により、
（77）
例へば、
① ２３４７５６１　＊
① ２‐３‐４７５‐６１　＊
であれば、
① ２＜７＞５＞１　＊
① ２＜４＞３＞１　＊
であると「見做し」、それ故、
① ２３４７５６１　＊
② ２５３４６７１　＊
④ ２７３４５６１　＊
⑤ ２７３６４５１　＊
⑥ ２４７５６３１　＊
⑫ ４２３６７５１　＊
⑯ ２３６４５７１　＊
⑰ ４２３５６７１　＊
⑲ ６２３４５７１　＊
⑳ ６２５３４７１　＊
といふ「順番」は、
① 　２４３１　　　＊
② 　２４３５１　　＊
④ 　２４３１　　　＊
⑤ 　２６３５４１　＊
⑥ 　２４６５３１　＊
⑫ ３２５４１　　　＊
⑯ 　２４３５１　　＊
⑰ ３２４１　　　　＊
⑲ ３２４１　　　　＊
⑳ ５２４３６１　　＊
といふ風に、「見做す」ことが出来る。
然るに、
（78）
① 　２囗囗１　　　＊
② 　２囗囗囗１　　＊
④ 　２囗囗１　　　＊
⑤ 　２囗囗囗囗１　＊
⑥ 　２囗囗囗囗１　＊
⑫ ３２囗囗１　　　＊
⑯ 　２囗囗囗１　　＊
⑰ ３２囗１　　　　＊
⑲ ３２囗１　　　　＊
⑳ ５２囗囗囗１　　＊
に於いて、囗≠１であって、囗≠２であるため、囗≧３ である。
従って、
（73）～（78）により、
（79）
① ２４３１　　　＊
② ２４３５１　　＊
④ ２４３１　　　＊
⑤ ２６３５４１　＊
⑥ ２４６５３１　＊
⑫ ３２５４１　　＊
⑯ ２４３５１　　＊
⑰ ３２４１　　　＊
⑲ ３２４１　　　＊
⑳ ５２４３６１　＊
といふ「順番」も、当然、
Ｎ＋１＜Ｎ＋Ａ＞Ｎ（ＮとＡは自然数で、Ａ≧２）
といふ「順番＊」を、含んでゐる。
然るに、
（80）
① ２４３１　　　＊
② ２４３５１　　＊
④ ２４３１　　　＊
⑤ ２６３５４１　＊
⑥ ２４６５３１　＊
⑫ ３２５４１　　＊
⑯ ２４３５１　　＊
⑰ ３２４１　　　＊
⑲ ３２４１　　　＊
⑳ ５２４３６１　＊
に対する「返り点」は、
① 二　四　三　一
② 二　四　三　五　一
④ 二　四　三　一
⑤ 二　下　三　上　四　一
⑥ 二　四　六　五　三　一
⑫ 三　二　五　四　一
⑯ 二　四　三　五　一
⑰ 三　二　四　一
⑲ 三　二　四　一
⑳ 五　二　四　三　六　一
である。
ｃｆ.

然るに、
（81）
③　 二　三　一　　＊
⑦ 二　三　一　　　＊
⑧ 二　三　四　一　＊
⑨ 二　下　一　上　＊
⑩ 二　四　三　一　＊
⑪ 三　一　四　二　＊
⑬ 三　二　四　一　＊
⑭ 二　三　  一　　＊
⑮ 三　四　二　一　＊
⑱ 下　二　上　一　＊
に加へて、
① 二　四　三　一　　　　　＊
② 二　四　三　五　一　　　＊
④ 二　四　三　一　　　　　＊
⑤ 二　下　三　上　四　一　＊
⑥ 二　四　六　五　三　一　＊
⑫ 三　二　五　四　一　　　＊
⑯ 二　四　三　五　一　　　＊
⑰ 四　二　五　一　　　　　＊
⑲ 三　二　四　一　　　　　＊
⑳ 五　二　四　三　六　一　＊
といふ「それら」は、
（ａ）『返り点』は、「下（右）から上（左）へ返る点」であって、「上（左）から下（右）へ返る点」ではない。
（ｂ）天・地点の間には甲・乙点が有り、甲・乙点の間には上・下点（か、一・二点）が有り、上・下点の間には一・二点が有る。
といふ「ルール」を「無視」してゐるため、『返り点』ではない。
然るに、
（82）
⑳ ４［３〔２（１）〕］
に於いて、
⑳ ２（　）⇒（　）２
⑳ ３〔　〕⇒〔　〕３
⑳ ４［　］⇒［　］４
といふ「倒置」を行ふと、
⑳ ４［３〔２（１）〕］⇒
⑳ ［〔（１）２〕３］４＝
⑳ 　　　１＜２＜３＜４。
といふ「ソート（並び替へ）」が、成立する。
従って、
（83）
⑩ ２（４３１）　＊
の『括弧』を、
⑩ ２（４［３〔１）〕］　＊
といふ「それ」に「書き換へ」た上で、
⑩ ２（　）⇒（　）２
⑩ ３〔　〕⇒〔　〕３
⑩ ４［　］⇒［　］４
といふ「倒置」を行ふと、
⑩ ２（４［３〔１）〕］⇒
⑩ （［〔１）２〕３］４＝
⑩ 　　　１＜２＜３＜４。
といふ「ソート（並び替へ）」が、成立する。
然るに、
（01）（02）（03）により、
（84）
⑳ ４［３〔２（１）〕］
⑩ ２（４［３〔１）〕］
に於いて、
⑳ ［〔（　）〕］ は、『括弧』であるが、
⑩ （［〔　）〕］ は、『括弧』ではない。
従って、
（85）
必ずしも、『括弧』である「必要」がない。のであれば、
① ２（４［３〔１）〕］
② ２（４［３〔５｛１）〕］｝
④ ２（４［３〔１）〕］
⑤ ２（６〈３〔５｛４［１）〕］｝〉
⑥ ２（４［６〈５｛３〔１）〕］｝〉
⑫ ３〔２（５｛４［１）〕］｝
⑯ ２（４［３〔５｛１）〕］｝
⑰ ３〔２（４［１）〕］
⑲ ３〔２（４［１）〕］
⑳ ５｛２（４［３〔６〈１）〕］｝〉
① ２‐３-４（７［５‐６〔１）〕］
② ２（５［３‐４〔６‐７｛１）〕］｝
④ ２（７［３‐４‐５‐６〔１）〕］
⑤ ２（７〈３〔６｛４‐５［１）〕］｝〉
⑥ ２（４［７〈５‐６｛３〔１）〕］｝〉
⑫ ４〔２‐３（６‐７｛５［１）〕］｝
⑯ ２‐３（６［４‐５〔７｛１）〕］｝
⑰ ４〔２‐３（５‐６‐７［１）〕］
⑲ ６〔２‐３‐４‐５（７［１）〕］
⑳ ６｛２（５［３‐４〔７〈１）〕］｝〉
といふ「括弧」により、
① （［〔１）２〕３］４
② （［〔｛１）２〕３］４｝５
④ （［〔１）２〕３］４
⑤ （〈〔｛［１）２〕３］４｝５〉６
⑥ （［〈｛〔１）２〕３］４｝５〉６
⑫ 〔（｛［１）２〕３］４｝５
⑯ （［〔｛１）２〕３］４｝５
⑰ 〔（［１）２〕３］４
⑲ 〔（［１）２〕３］４
⑳ ｛（［〔〈１）２〕３］４｝５〉６
① （［〔１）２‐３-４〕５‐６］７
② （［〔｛１）２〕３‐４］５｝６‐７
④ （［〔１）２〕３‐４‐５‐６］７
⑤ （〈〔｛［１）２〕３］４‐５｝６〉７
⑥ （［〈｛〔１）２〕３］４｝５-６〉７
⑫ ［（〔〈｛１）２〕３］４｝５〉６‐７
⑯ （［〔｛１）２‐３〕４‐５］６｝７
⑰ 〔（［１）２‐３〕４］５‐６‐７
⑲ 〔（［１）２‐３‐４‐５〕６］７
⑳ ｛（［〔〈１）２〕３‐４］５｝６〉７
といふ「順番」を表すことも、出来ないわけではない。
然るに、
（01）（02）により、
（86）
① １２３４７５６
② １２５３４６７
④ １２７３４５６
⑤ １２７３６４５
⑥ ３１２４７５６
⑫ ５１４２３６７
⑯ ７１２３６４５
⑰ ７１４２５３６
⑲ ７１６２３４５
⑳ ７１６２５３４
に対する、
① （　）
② （　）
④ （　）
⑤ 〔（  ）〕
⑥ （　）（　）
⑫ 〔（　）〕
⑯ 〔（　）〕
⑰ 〔（　）〕
⑲ 〔（　）〕
⑳ ［〔（　）〕］
が、『括弧』であるのに対して、
① ２４３１　　　＊
② ２４３５１　　＊
④ ２４３１　　　＊
⑤ ２６３５４１　＊
⑥ ２４６５３１　＊
⑫ ３２５４１　　＊
⑯ ２４３５１　　＊
⑰ ３２４１　　　＊
⑲ ３２４１　　　＊
⑳ ５２４３６１　＊
に対する、
① （［〔　）〕］
② （［〔｛　）〕］｝
④ （［〔　）〕］
⑤ （〈〔｛［　）〕］｝〉
⑥ （［〈｛〔　）〕］｝〉
⑫ 〔（｛［　）〕］｝
⑯ （［〔｛　）〕］｝
⑰ 〔（［　）〕］
⑲ 〔（［　）〕］
⑳ ｛（［〔〈　）〕］｝〉
といふ「それ」は、もちろん、『括弧』ではない。
従って、
（73）（79）（81）（86）により、
（87）
① ２３４７５６１　＊
② ２５３４６７１　＊
④ ２７３４５６１　＊
⑤ ２７３６４５１　＊
⑥ ２４７５６３１　＊
⑫ ４２３６７５１　＊
⑯ ２３６４５７１　＊
⑰ ４２３５６７１　＊
⑲ ６２３４５７１　＊
⑳ ６２５３４７１　＊
といふ「順番」は、
Ｎ＋１＜Ｎ＋Ａ＞Ｎ（ＮとＡは自然数で、Ａ≧２）
といふ「順番＊」を、含んでゐて、尚かつ、『括弧・返り点』を付けることが出来ない。
従って、
（71）（87）により、
（88）
① １２４３
② １３２４
④ １４２３
⑤ １４３２
⑥ ２１４３
⑫ ３２１４
⑯ ４１３２
⑰ ４２１３
⑲ ４３１２
⑳ ４３２１
③ １３４２　＊
⑦ ２３１４　＊
⑧ ２３４１　＊
⑨ ２４１３　＊
⑩ ２４３１　＊
⑪ ３１４２　＊
⑬ ３２４１　＊
⑭ ３４１２　＊
⑮ ３４２１　＊
⑱ ４２３１　＊
① １２３４７５６
② １２５３４６７
④ １２７３４５６
⑤ １２７３６４５
⑥ ３１２４７５６
⑫ ５１４２３６７
⑯ ７１２３６４５
⑰ ７１４２３５６
⑲ ７１６２３４５
⑳ ７１６２５３４
といふ「３０個の順番」に対して、
① ２３４７５６１　＊
② ２５３４６７１　＊
④ ２７３４５６１　＊
⑤ ２７３６４５１　＊
⑥ ２４７５６３１　＊
⑫ ４２３６７５１　＊
⑯ ２３６４５７１　＊
⑰ ４２３５６７１　＊
⑲ ６２３４５７１　＊
⑳ ６２５３４７１　＊
といふ「１０個の順番」が加はった、「４０個の順番」が与へられた際に、これらの内の「任意の順番」は、
Ｎ＋１＜Ｎ＋Ａ＞Ｎ（ＮとＡは自然数で、Ａ≧２）
といふ「順番＊」を含んでゐない。ならば、その時に限って、『括弧・返り点』を付けることが、出来る。
従って、
（89）
『括弧』　によって表すことが出来ない「返読の順番＊の集合」は、
『返り点』によって表すことが出来ない「返読の順番＊の集合」に等しい。
従って、
（90）
『括弧』　によって表すことが出来る「返読の順番の集合」は、
『返り点』によって表すことが出来る「返読の順番の集合」に等しい。
従って、
（88）（90）により、
（91）
① １２４３
② １３２４
④ １４２３
⑤ １４３２
⑥ ２１４３
⑫ ３２１４
⑯ ４１３２
⑰ ４２１３
⑲ ４３１２
⑳ ４３２１
① １２３４７５６
② １２５３４６７
④ １２７３４５６
⑤ １２７３６４５
⑥ ３１２４７５６
⑫ ５１４２３６７
⑯ ７１２３６４５
⑰ ７１４２３５６
⑲ ７１６２３４５
⑳ ７１６２５３４
に対する、
① レ
② レ
④ 二　一
⑤ レ　レ
⑥ レ　レ
⑫ レ　レ
⑯ 二　一レ
⑰ 二　レ　一
⑲ レ　二　一
⑳ レ　レ　レ
① 二　一
② 二　一
④ 二　一
⑤ 三　二　一
⑥ 二　一　二　一
⑫ 三　二　一
⑯ 三　二　一
⑰ 下　二　一　上
⑲ 三　二　一
⑳ 四　三　二　一
は、『返り点』であって、
① １２４（３）
② １３（２）４
④ １４（２３）
⑤ １４〔３（２）〕
⑥ ２（１）４（３）
⑫ ３〔２（１）〕４
⑯ ４〔１３（２）〕
⑰ ４〔２（１）３〕
⑲ ４〔３（１２）〕
⑳ ４［３〔２（１）〕］
① １２３４７（５６）
② １２５（３４）６７
④ １２７（３４５６）
⑤ １２７〔３６（４５）〕
⑥ ３（１２）４７（５６）
⑫ ５〔１４（２３）〕６７
⑯ ７〔１２３６（４５）〕
⑰ ７〔１４（２３）５６〕
⑲ ７〔１６（２３４５）〕
⑳ ７［１６〔２５（３４）〕］
は、『括弧』である。
（92）
⑰ 有読書者＝
⑰ 書を読む者有り。
といふ「漢文」には、
⑰ 有〔読（書）者〕。
といふ「補足構造」が、初めから有って、その一方で、
漢語における語順は、国語と大きく違っているところがある。すなわち、その補足構造における語順は、国語とは全く反対である（鈴木直治、
中国語と漢文、1975年、二九六頁）。
とすれば、
⑰ 有読書者＝
⑰ 有〔読（書）者〕＝
⑰ ４〔２（１）３〕⇒
⑰ 〔（１）２３〕４＝
⑰ 〔（書）読者〕有＝
⑰ 〔（書を）読む者〕有り。
といふ「漢文訓読」が成立することは、「当然」である。
然るに、
（93）
このやうな「事情」が、「全ての漢文訓読」に於いて、成立してゐるとすれば、
（　）
〔　〕
［　］
｛　｝
といふ「括弧」と、
レ
二　一レ
下　上レ
乙　甲レ
地　天レ
一　二　三　四　五　・　・　・　・　・
上　中　下
甲　乙　丙　丁　戊　・　・　・　・　・
天　地　人
といふ「返り点」の間に、「過不足」が生じない限り、
『返り点』が表す「返読の順番」を、『括弧』でも表すことが出来ることは、当然である。
平成２８年０４月２４日、毛利太。
　― 関連サイト ―
（01）『括弧』と『返り点』と「白話文」。　：http://kannbunn.blogspot.com/2016/04/blog-post_34.html
（02）『括弧・返り点』の研究（Ⅲ）。　　　：http://kannbunn.blogspot.com/2016/05/blog-post_5.html
（03）「返り点」を完璧に説明します。　　　：http://kannbunn.blogspot.com/2016/03/blog-post_31.html
（04）「返り点」と「括弧」と「補足構造」。：http://kannbunn.blogspot.com/2016/05/blog-post_39.html