NHK高校講座 数学I(仮説検定)
(02)
一枚のコインを、10回トスするとして、
① 0回、表が出る場合の数=10C 0= 1
② 1回、表が出る場合の数=10C 1= 10
③ 2回、表が出る場合の数=10C 2= 45
④ 3回、表が出る場合の数=10C 3=120
⑤ 4回、表が出る場合の数=10C 4=210
⑥ 5回、表が出る場合の数=10C 5=252
⑦ 6回、表が出る場合の数=10C 6=210
⑧ 7回、表が出る場合の数=10C 7=120
⑨ 8回、表が出る場合の数=10C 8= 45
⑩ 9回、表が出る場合の数=10C 9= 10
⑪ 10回、表が出る場合の数=10C10= 1
然るに、
(03)
一枚のコインを、10回トスするとして、
⑫「表か裏」が出る場合の数=①+②+③+④+⑤+⑥+⑦+⑧+⑨+⑩+⑪=1024
従って、
(02)(03)により、
(04)
一枚のコインを、10回トスするとして、
① 0回、表が出る確率= 1/1024
② 1回、表が出る確率=10/1024
③ 2回、表が出る確率=45/1024
然るに、
(05)
という「公式」を「計算」すると、
② 1回、表が出る確率=10×(1/2)の10乗=10/1024
従って、
(04)(05)により、
(06)
(01)~(07)により、
(08)
(ⅰ)
「1枚のコインを10回投げたところ、表が1回しか出なかった。このコインは細工されていると言えるか?」
ということを、明らかにするために、「コインは細工されていない(1/2の確率で裏表が出る)」という「帰無仮説」を「仮定」する。
然るに、
(ⅱ)
「コインが細工されていない」と「仮定」すると、1枚のコインを10回投げて、表が1回しか出ない「確率」は「1%にも満たない」。
然るに、
(ⅲ)
「1%にも満たない」ということは、「ほぼ、有り得ない」。
従って、
(ⅱ)(ⅲ)により、
(ⅳ)
「背理法(RAA)」により、「コインが細工されていない」という「仮定」は、「棄却(否定)」される。
従って、
(ⅴ)
「コインは細工されていない(帰無仮説)」は「マチガイ」であって、「二重否定(DN)」により、
「コインは細工されている (対立仮設)」こそが、「正しい」。
従って、
(08)により、
(09)
「仮説検定」というのは、
「帰無仮説」と「対立仮説」という
「二つの矛盾する仮定」を「仮定」した上で、
「帰無仮説」が起こる「確率」を計算して、
「その確率」が、「一定の数値(有意水準)」よりも低ければ、
「帰無仮説」を「否定(棄却)」することによって、
「対立仮説」を「肯定」する「手法」である。
然るに、
(10)
P<0.05は慣習的なものだ。P<0.05を有意水準とする数学的な根拠は無くて、P<0.1でもP<0.03でも構わないが、P<0.05以外を有意水準にするときは、根拠を問われることになる。
(P値と有意水準 | ブログ | 統計WEB)
然るに、
(11)
P<0.05は慣習的なものだ。
とは言うものの、
P≦0.5(半々以下)
であれば、「帰無仮説」を「否定(棄却)」出来ないわけであって、そのため、
P値が、低ければ低いほど、「信頼性」が増すことになることは、当然である。
従って、
(12)
たとえば、P値<0.01の結果が出たときに、「非常に有意」という結論を出している学会発表をみたことはないでしょうか?私はしばしばみかけますが、」「非常に有意」という言葉は、実は有り得ないのです。英検で「すごく合格」という結果が出てくるようなものだからです。
(吉田寛輝、いちばんやさしい医療統計、2019年、50頁)
とは言うものの、私自身は、「非常に有意」という「言い方」をすることは、当然であると、思っている。
然るに、
(13)
(a)
(b)
従って、
(13)により、
(14)
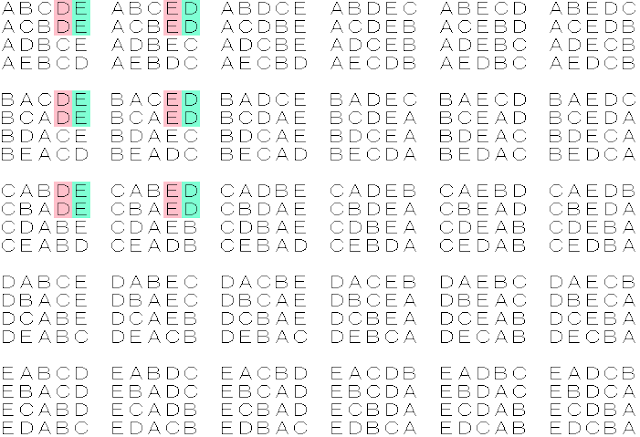
男子={A,B,C}
女子={D,E}
であるとして、
男子と女子が、ランダムに、「1列」に並ぶ際に、
女子={D,E}
の2人が、「4番目と5番目に並ぶ、確率」は、
(3!×2!)÷5!=12÷120=0.1
であって、
女子={D,E}
の内の1人が「5番目に並ぶ、確率」は、
(4!×2!)÷5!=48÷120=0.4
である。
従って、
(14)により、
(15)
男子=36人
女子= 5人
の「クラス」で、男子と女子が、ランダムに、「1列」に並ぶ際に、
女子= 5人
が、「37・38・39・40・41番目に並ぶ、確率」は、
(36!×5!)÷41!=約0.0000013344(約75万分の1)
である。
従って、
(05)(06)(15)により、
(16)
① 1枚のコインを10回投げて、表が1回だけしか出ない 「確率」=約0.0977
② 5人の女子が、37・38・39・40・41番目に並ぶ「確率」=約0.0000013344
に於いて、
② の方が、
① よりも、「比較にならない」程「小さい」。
然るに、
(17)
という「データ」を、「大きい順に並べ替える」と、 従って、
(15)(16)(17)により、
(18)
点滴無し=36回
点滴有り= 5回
の「血液検査」の「赤血球のデータ」を、「大きい順の並べた」際に、
点滴有り= 5回
の「データ」が、「37・38・39・40・41番目に並んだ」とするならば、その場合は、
『点滴をしても、赤血球の数値は下がらない。』という「帰無仮説」は、「棄却」せざるを得ない。
然るに、
(19)従って、
(18)(19)により、
(20)
『赤血球が少なくなっているのは、点滴で血液が薄くなっている可能性がある。』
という「対立仮説」こそが、「正しい」。
然るに、
(21)
『赤血球が少なくなっているのは、点滴で血液が薄くなっている』からであるとするならば、
「点滴・無し」の際の、「赤血球のデータ」は、「外れ値」として、「除外」しなければ、
従って、
(13)により、
(14)
男子={A,B,C}
女子={D,E}
であるとして、
男子と女子が、ランダムに、「1列」に並ぶ際に、
女子={D,E}
の2人が、「4番目と5番目に並ぶ、確率」は、
(3!×2!)÷5!=12÷120=0.1
であって、
女子={D,E}
の内の1人が「5番目に並ぶ、確率」は、
(4!×2!)÷5!=48÷120=0.4
である。
従って、
(14)により、
(15)
男子=36人
女子= 5人
の「クラス」で、男子と女子が、ランダムに、「1列」に並ぶ際に、
女子= 5人
が、「37・38・39・40・41番目に並ぶ、確率」は、
(36!×5!)÷41!=約0.0000013344(約75万分の1)
である。
従って、
(05)(06)(15)により、
(16)
① 1枚のコインを10回投げて、表が1回だけしか出ない 「確率」=約0.0977
② 5人の女子が、37・38・39・40・41番目に並ぶ「確率」=約0.0000013344
に於いて、
② の方が、
① よりも、「比較にならない」程「小さい」。
然るに、
(17)
という「データ」を、「大きい順に並べ替える」と、 従って、
(15)(16)(17)により、
(18)
点滴無し=36回
点滴有り= 5回
の「血液検査」の「赤血球のデータ」を、「大きい順の並べた」際に、
点滴有り= 5回
の「データ」が、「37・38・39・40・41番目に並んだ」とするならば、その場合は、
『点滴をしても、赤血球の数値は下がらない。』という「帰無仮説」は、「棄却」せざるを得ない。
然るに、
(19)従って、
(18)(19)により、
(20)
『赤血球が少なくなっているのは、点滴で血液が薄くなっている可能性がある。』
という「対立仮説」こそが、「正しい」。
然るに、
(21)
『赤血球が少なくなっているのは、点滴で血液が薄くなっている』からであるとするならば、
「点滴・無し」の際の、「赤血球のデータ」は、「外れ値」として、「除外」しなければ、
ということが言えるのかどうかは、「分からない」。
然るに、
(22)
従って、、
(22)により、
(23)
「36回の血液検査」の際にあって、
「2019年01月25日」の「赤血球の値(2.46)」という「値」は、
「中央値(2.51)」よりも「小さい」し、
「平均値(2.48)」よりも「小さい」。
従って、
(21)(22)(23)により、
(24)
「点滴をやめて様子をみたが、01月25日の血液検査で、血液濃縮(脱水)による腎機能の低下が認められた」とは言うものの、仮に、
「点滴をやめた結果として、脱水(血液濃縮)が起こっていた」とするならば、
「36回の血液検査」の内、少なくとも、その「3分の2」である、
「24回の血液検査」に於いても、「脱水(血液濃縮)」があった。
ということに、ならざるを得ない。
然るに、
(25)
「赤血球の値(2.46)」という「値」は、「基準値の下限(4.27)」の、
「60%」にも満たない(胃癌手術後の悪性貧血)である上に、S医師ではなく、本来の主治医であるK医師からは、「脱水(血液濃縮)」に関する「説明」を受けたことなど、ただの一度も無い。
従って、
(23)(24)(25)により、
(26)
「36回の血液検査」の際にあって、
「2019年01月25日」の「赤血球の値(2.46)」という「値」は、
「中央値(2.51)」よりも「小さい」し、
「平均値(2.48)」よりも「小さい」という「事実」を以てすれば、
「2019年01月25日」に於いて、『脱水』があった。
ということは、「有り得ない」ということを、「裁判」では「主張」するつもりである。
然るに、
(27)
「同日(2019年01月27日)」より「輸液(点滴)」を再開した「結果」、どうなったかと言うと、従って、
(27)により、
(28)
(Ⅰ)
赤血球は、
「2019年01月29日」には、
「2019年01月18日」と「同じレベル」に戻っている。
(Ⅱ)
尿素窒素は、
「2019年01月18日」から、
「2019年01月25日」にかけて、「3倍強」に跳ね上がっていて、
「点滴」を「再開」した後の、
「2019年01月29日」になっても、
「2019年01月18日」の「2.5倍」のままである。
(Ⅲ)
クレアチニンは、
「2019年01月18日」から、
「2019年01月25日」にかけて、「1.74倍」になっていて、
「点滴」を「再開」した後の、
「2019年01月29日」には、反って、更に、「上昇」し、
「2019年01月18日」の「1.86倍」になっている。
(Ⅳ)
その「結果」として、父は、
「2019年01月29日、22時21分」に「永眠」した。
令和04年06月27日、毛利太。
然るに、
(22)
従って、、
(22)により、
(23)
「36回の血液検査」の際にあって、
「2019年01月25日」の「赤血球の値(2.46)」という「値」は、
「中央値(2.51)」よりも「小さい」し、
「平均値(2.48)」よりも「小さい」。
従って、
(21)(22)(23)により、
(24)
「点滴をやめて様子をみたが、01月25日の血液検査で、血液濃縮(脱水)による腎機能の低下が認められた」とは言うものの、仮に、
「点滴をやめた結果として、脱水(血液濃縮)が起こっていた」とするならば、
「36回の血液検査」の内、少なくとも、その「3分の2」である、
「24回の血液検査」に於いても、「脱水(血液濃縮)」があった。
ということに、ならざるを得ない。
然るに、
(25)
「赤血球の値(2.46)」という「値」は、「基準値の下限(4.27)」の、
「60%」にも満たない(胃癌手術後の悪性貧血)である上に、S医師ではなく、本来の主治医であるK医師からは、「脱水(血液濃縮)」に関する「説明」を受けたことなど、ただの一度も無い。
従って、
(23)(24)(25)により、
(26)
「36回の血液検査」の際にあって、
「2019年01月25日」の「赤血球の値(2.46)」という「値」は、
「中央値(2.51)」よりも「小さい」し、
「平均値(2.48)」よりも「小さい」という「事実」を以てすれば、
「2019年01月25日」に於いて、『脱水』があった。
ということは、「有り得ない」ということを、「裁判」では「主張」するつもりである。
然るに、
(27)
「同日(2019年01月27日)」より「輸液(点滴)」を再開した「結果」、どうなったかと言うと、従って、
(27)により、
(28)
(Ⅰ)
赤血球は、
「2019年01月29日」には、
「2019年01月18日」と「同じレベル」に戻っている。
(Ⅱ)
尿素窒素は、
「2019年01月18日」から、
「2019年01月25日」にかけて、「3倍強」に跳ね上がっていて、
「点滴」を「再開」した後の、
「2019年01月29日」になっても、
「2019年01月18日」の「2.5倍」のままである。
(Ⅲ)
クレアチニンは、
「2019年01月18日」から、
「2019年01月25日」にかけて、「1.74倍」になっていて、
「点滴」を「再開」した後の、
「2019年01月29日」には、反って、更に、「上昇」し、
「2019年01月18日」の「1.86倍」になっている。
(Ⅳ)
その「結果」として、父は、
「2019年01月29日、22時21分」に「永眠」した。
令和04年06月27日、毛利太。