「対偶と逆」を「（式ではなく）言葉」で説明する。

（01）
①（Ｐであるならば、Ｑである）。
②（Ｐであって、　　Ｑでない）といふことはない。
に於いて、
①＝② である。
然るに、
（02）
②（Ｐであって、Ｑでない）といふことはない。
③（Ｑでなくて、Ｐである）といふことはない。
に於いて、
②＝③ である。
然るに、
（03）
③（Ｑでなくて、　　Ｐである）といふことはない。
④（Ｑでないならば、Ｐでない）。
に於いて、
③＝④ である。
従って、
（01）（02）（03）により、
（04）
①（Ｐであるならば、Ｑである）。
②（Ｐであって、　　Ｑでない）といふことはない。
③（Ｑでなくて、　　Ｐである）といふことはない。
④（Ｑでないならば、Ｐでない）。
に於いて、
①＝②＝③＝④ である。
従って、
（04）により、
（05）
①（Ｐであるならば、Ｑである）。
④（Ｑでないならば、Ｐでない）。
に於いて、
①＝④ である。
然るに、
（06）
①（Ｐであるならば、Ｑである）。
④（Ｑでないならば、Ｐでない）。
に於いて、
① は「④の対偶」であって、
④ は「①の対偶」である。
従って、
（06）により、
（07）
「対偶は、互いに、等しい。」
然るに、
（08）
①（Ｐであるならば、Ｑである）。
②（Ｑであるならば、Ｐである）。
③（Ｐでないならば、Ｑでない）。
に於いて、
②＝③ は「対偶」である。
然るに、
（09）
①（Ｐであるならば、Ｑである）。
③（Ｐでないならば、Ｑでない）。
に於いて、
①＝③ である。
とは、「限らない」。
従って、
（08）（09）により、
（10）
①（Ｐであるならば、Ｑである）。
②（Ｑであるならば、Ｐである）。
に於いても、
①＝② である。
とは、「限らない」。
従って、
（10）により、
（11）
①（Ｐであるならば、Ｑである）。
②（Ｑであるならば、Ｐである）。
に於いて、
① が「真（本当）」である。
からと言って、
② も「真（本当）」である。
とは、「限らない」。
従って、
（11）により、
（12）
「ある仮言命題が、真である。」からと言って、
「逆の仮言命題も、真である。」とは限らない。
従って、
（13）
「逆は、必ずしも、真ではない。」
令和０４年１１月１９日、毛利太。

「パースの法則」の「言ひ換へ」（Ⅱ）。

（01）
（ⅰ）
１　　（１）　　（Ｐ→Ｑ）→Ｐ　Ａ
１　　（２）　～（Ｐ→Ｑ）∨Ｐ　１含意の定義
　３　（３）　～（Ｐ→Ｑ）　　　Ａ
　３　（４）～（～Ｐ∨Ｑ）　　　Ａ
　３　（５）　　Ｐ＆～Ｑ　　　　４ド・モルガンの法則
　３　（６）　（Ｐ＆～Ｑ）∨Ｐ　５∨Ｉ
　　７（７）　　　　　　　　Ｐ　Ａ
　　７（８）　（Ｐ＆～Ｑ）∨Ｐ　７∨Ｉ
１　　（９）　（Ｐ＆～Ｑ）∨Ｐ　１３６７８∨Ｅ
（ⅱ）
１　　（１）　（Ｐ＆～Ｑ）∨Ｐ　Ａ
　２　（２）　（Ｐ＆～Ｑ）　　　Ａ
　２　（３）～（～Ｐ∨Ｑ）　　　２ド・モルガンの法則
　２　（４）　～（Ｐ→Ｑ）　　　３含意の定義
　２　（５）　～（Ｐ→Ｑ）∨Ｐ　４∨Ｉ
　　６（６）　　　　　　　　Ｐ　Ａ
　　６（７）　～（Ｐ→Ｑ）∨Ｐ　６∨Ｉ
１　　（８）　～（Ｐ→Ｑ）∨Ｐ　１２５６７∨Ｅ
１　　（９）　　（Ｐ→Ｑ）→Ｐ　８含意の定義
従って、
（01）により、
（02）
①（Ｐ→　Ｑ）→Ｐ
②（Ｐ＆～Ｑ）∨Ｐ
に於いて、
①＝② である。
（03）
（ⅱ）
１　　（１）（Ｐ＆～Ｑ）∨Ｐ　Ａ
　２　（２）　Ｐ＆～Ｑ　　　　Ａ
　２　（３）　Ｐ　　　　　　　２＆Ｅ
　２　（４）　Ｐ∨Ｐ　　　　　３∨Ｉ
　２　（５）　　　～Ｑ　　　　２＆Ｅ
　２　（６）　～Ｑ∨Ｐ　　　　５∨Ｉ
　２　（７）（Ｐ∨Ｐ）＆
　　　　　　（～Ｑ∨Ｐ）　　　４６＆Ｉ
　　８（８）　　　　　　Ｐ　　Ａ
　　８（９）　　　　Ｐ∨Ｐ　　８∨Ｉ
　　８（ア）　　　　～Ｑ∨Ｐ　８∨Ｉ
　　８（イ）（Ｐ∨Ｐ）＆
　　　　　（～Ｑ∨Ｐ）　　　　９ア＆Ｉ
（ⅲ）
１　　（１）　（Ｐ∨Ｐ）＆
　　　　　　（～Ｑ∨Ｐ）　　　　Ａ
１　　（２）　　Ｐ∨Ｐ　　　　　１＆Ｅ
１　　（３）～～Ｐ∨Ｐ　　　　　２ＤＮ
１　　（４）　～Ｐ→Ｐ　　　　　３含意の定義
　５　（５）　　　～Ｐ　　　　　Ａ
１５　（６）　　　　Ｐ　　　　　４５ＭＰＰ
１　　（７）　～Ｑ∨Ｐ　　　　　１＆Ｅ
１　　（８）　　Ｑ→Ｐ　　　　　７含意の定義
１５　（９）　　　～Ｑ　　　　　５８ＭＴＴ
１５　（ア）　Ｐ＆～Ｑ　　　　　６９＆Ｉ
１　　（イ）～Ｐ→（Ｐ＆～Ｑ）　５アＣＰ
１　　（ウ）　Ｐ∨（Ｐ＆～Ｑ）　イ含意の定義
１　　（エ）（Ｐ＆～Ｑ）∨Ｐ　　ウ交換法則
従って、
（03）により、
（04）
②（Ｐ＆～Ｑ）∨Ｐ
③（Ｐ∨Ｐ）＆（～Ｑ∨Ｐ）
に於いて、
②＝③ である（分配の法則）。
然るに、
（05）
（ⅲ）
１　　（１）（Ｐ∨Ｐ）＆（～Ｑ∨Ｐ）　Ａ
１　　（２）　Ｐ∨Ｐ　　　　　　　　　Ａ
　３　（３）　Ｐ　　　　　　　　　　　Ａ
　　４（４）　　　Ｐ　　　　　　　　　Ａ
１　　（５）　Ｐ　　　　　　　　　　　１３３４４∨Ｅ
１　　（６）　　　　　　　～Ｑ∨Ｐ　　１＆Ｅ
１　　（７）　　　　　　　Ｐ∨～Ｑ　　６交換法則
１　　（８）（Ｐ∨～Ｑ）＆Ｐ　　　　　５７＆Ｉ
（ⅳ）
１　　（１）（Ｐ∨～Ｑ）＆Ｐ　　　　　Ａ
１　　（２）　Ｐ∨～Ｑ　　　　　　　　１＆Ｅ
１　　（３）　～Ｑ∨Ｐ　　　　　　　　２交換法則
１　　（４）　　　　　　　Ｐ　　　　　１＆Ｅ
１　　（５）　　　　　Ｐ∨Ｐ　　　　　４∨Ｉ
１　　（６）（Ｐ∨Ｐ）＆（～Ｑ∨Ｐ）　３５＆Ｉ
従って、
（05）により、
（06）
③（Ｐ∨Ｐ）＆（～Ｑ∨Ｐ）
④（Ｐ∨～Ｑ）＆Ｐ
に於いて、
③＝④ である。
従って、
（02）（04）（06）により、
（07）
①（Ｐ→　Ｑ）→Ｐ
②（Ｐ＆～Ｑ）∨Ｐ
③（Ｐ∨Ｐ）＆（～Ｑ∨Ｐ）
④（Ｐ∨～Ｑ）＆Ｐ
に於いて、
①＝② であって、
②＝③ であって、
③＝④ である。
従って、
（07）により、
（08）
①（Ｐ→　Ｑ）→Ｐ
②（Ｐ＆～Ｑ）∨Ｐ
③（Ｐ∨～Ｑ）＆Ｐ
に於いて、
①＝②＝③ である。
従って、
（08）により、
（09）
①（（Ｐ→　Ｑ）→Ｐ）→Ｐ
②（（Ｐ＆～Ｑ）∨Ｐ）→Ｐ
③（（Ｐ∨～Ｑ）＆Ｐ）→Ｐ
に於いて、
①＝②＝③ である。
従って、
（09）により、
（10）
①（（ＰならばＱ）ならばＰ）ならばＰである。
②（（Ｐであって、Ｑでないか）、または、Ｐである）ならばＰである。
③（（Ｐであるか、または、Ｑではない）としても、Ｐである）ならばＰである。
に於いて、
①＝②＝③ である。
従って、
（11）
①（（日本人ならば男性）ならば日本人）ならば日本人である。
②（（日本人であって、女性であるか）、または、日本人である）ならば日本人である。
③（（日本人であるか、または、女性である）としても、日本人である）ならば日本人である。
に於いて、
①＝②＝③ である。
然るに、
（12）
命題計算では、パースの法則は （（Ｐ→Ｑ）→Ｐ）→Ｐ のことを言う。この意味するところを書き出すと、命題Ｐについて、命題Ｑが存在して、「ＰならばＱ」からＰが真であることが従うときには、Ｐは真でなければならないとなる。とりわけ、Ｑとして偽を選んだ場合には、Ｐから偽が従うときは常にＰが真であるならば、Ｐは真であるとなる（ウィキペディア）。
従って、
（11）（12）により、
（13）
①「パースの法則」は、例へば、
②（（日本人であって、女性であるか）、または、日本人である）ならば日本人である。
③（（日本人であるか、または、女性である）にせよ、日本人である）ならば日本人である。
といふ「命題」に「等しい」。
令和０４年１１月１１日、毛利太。

「パースの法則」の「言ひ換へ」。

（01）
命題計算では、パースの法則は （（Ｐ→Ｑ）→Ｐ）→Ｐ のことを言う。この意味するところを書き出すと、命題Ｐについて、命題Ｑが存在して、「ＰならばＱ」からＰが真であることが従うときには、Ｐは真でなければならないとなる。とりわけ、Ｑとして偽を選んだ場合には、Ｐから偽が従うときは常にＰが真であるならば、Ｐは真であるとなる（ウィキペディア）。
従って、
（01）により、
（02）
（（Ｐ→Ｑ）→Ｐ）→Ｐ
といふ「恒真式（トートロジー）」を「パースの法則」と言ふ。
従って、
（01）（02）により、
（03）
（（ＰならばＱ）ならばＰ）ならばＰである。
といふ「それ」を、「パースの法則」といふ。
然るに、
（04）
１　　（１）　　　　（Ｐ→Ｑ）→Ｐ　Ａ
１　　（２）　　　～（Ｐ→Ｑ）∨Ｐ　１含意の定義
　３　（３）　　　～（Ｐ→Ｑ）　　　Ａ
　３　（４）　　～（～Ｐ∨Ｑ）　　　Ａ
　３　（５）　　　　Ｐ＆～Ｑ　　　　４ド・モルガンの法則
　３　（６）　　　　Ｐ　　　　　　　５＆Ｅ
　　７（７）　　　　　　　　　　Ｐ　Ａ
１　　（８）　　　　　　　　　　Ｐ　１３６７７∨Ｅ
　　　（９）（（Ｐ→Ｑ）→Ｐ）→Ｐ　１８ＣＰ
従って、
（04）により、
（05）
１　　（１）（Ｐ→Ｑ）→Ｐ　Ａ
　２　（２）　　　　　～Ｐ　Ａ
からは、「Ｐ」が『導出』されなければ、ならない。
然るに、
（06）
１　（１）　　（Ｐ→Ｑ）→Ｐ　　　Ａ
　２（２）　　　　　　　～Ｐ　　　Ａ
１２（３）　～（Ｐ→Ｑ）　　　　　１２ＭＰＰ
１２（４）～（～Ｐ∨Ｑ）　　　　　３含意の定義
１２（５）　　Ｐ＆～Ｑ　　　　　　４含意の定義
１２（６）　　Ｐ　　　　　　　　　５＆Ｅ
１２（７）　　Ｐ＆～Ｐ　　　　　　２６＆Ｉ
１　（８）　　　　　　～～Ｐ　　　２７ＲＡＡ
１　（９）　　　　　　　　Ｐ　　　８ＤＮ
　　（ア）（（Ｐ→Ｑ）→Ｐ）→Ｐ　１９ＣＰ
従って、
（05）（06）により、
（07）
果たして、
１　　（１）（Ｐ→Ｑ）→Ｐ　Ａ
　２　（２）　　　　　～Ｐ　Ａ
からは、「Ｐ」が『導出』される。
然るに、
（08）
（ⅰ）
１　　（１）　　（Ｐ→Ｑ）→Ｐ　Ａ
１　　（２）　～（Ｐ→Ｑ）∨Ｐ　１含意の定義
　３　（３）　～（Ｐ→Ｑ）　　　Ａ
　３　（４）～（～Ｐ∨Ｑ）　　　Ａ
　３　（５）　　Ｐ＆～Ｑ　　　　４ド・モルガンの法則
　３　（６）　（Ｐ＆～Ｑ）∨Ｐ　５∨Ｉ
　　７（７）　　　　　　　　Ｐ　Ａ
　　７（８）　（Ｐ＆～Ｑ）∨Ｐ　７∨Ｉ
１　　（９）　（Ｐ＆～Ｑ）∨Ｐ　１３６７８∨Ｅ
（ⅱ）
１　　（１）　（Ｐ＆～Ｑ）∨Ｐ　Ａ
　２　（２）　（Ｐ＆～Ｑ）　　　Ａ
　２　（３）～（～Ｐ∨Ｑ）　　　２ド・モルガンの法則
　２　（４）　～（Ｐ→Ｑ）　　　３含意の定義
　２　（５）　～（Ｐ→Ｑ）∨Ｐ　４∨Ｉ
　　６（６）　　　　　　　　Ｐ　Ａ
　　６（７）　～（Ｐ→Ｑ）∨Ｐ　６∨Ｉ
１　　（８）　～（Ｐ→Ｑ）∨Ｐ　１２５６７∨Ｅ
１　　（９）　　（Ｐ→Ｑ）→Ｐ　８含意の定義
従って、
（08）により、
（09）
①（Ｐ→　Ｑ）→Ｐ
②（Ｐ＆～Ｑ）∨Ｐ
に於いて、
①＝② である。
従って、
（09）により、
（10）
①（（Ｐ→　Ｑ）→Ｐ）→Ｐ
②（（Ｐ＆～Ｑ）∨Ｐ）→Ｐ
に於いても、
①＝② である。
従って、
（10）により、
（11）
①（（ＰならばＱ）ならばＰ）ならばＰである。
②（（Ｐであって、Ｑである）か、または、Ｐ）ならばＰである。
に於いて、
①＝② である。
然るに、
（12）
①（（ＰならばＱ）ならばＰ）ならばＰである。
②（（Ｐであって、Ｑである）か、または、Ｐ）ならばＰである。
に於いて、
① は、「難解」であるが、
② は、「平易」である。
然るに、
（13）
命題Ｐについて、命題Ｑが存在して、「ＰならばＱ」からＰが真であることが従うときには、Ｐは真でなければならないとなる。とりわけ、Ｑとして偽を選んだ場合には、Ｐから偽が従うときは常にＰが真であるならば、Ｐは真であるとなる（ウィキペディア）。
といふ「言ひ方」は、私にとって、
①（（ＰならばＱ）ならばＰ）ならばＰである。
といふ「言ひ方」と、「同じくらひ」に、「難解」である。
（14）
②（（日本人であって、男性である）か、または、日本人）ならば日本人である。
③（（日本人であって、男性でない）か、または、日本人）ならば日本人である。
に於いて、
② は「真」であるし、
③ も「真」である。
従って、
（03）（11）（14）により、
（15）
①（（日本人ならば男性）ならば日本人）ならば日本人である。
②（（日本人ならば女性）ならば日本人）ならば日本人である。
に於いて、
① は「パースの法則」であって、
② も「パースの法則」である。
令和０４年１１月１０日、毛利太。

「含意の定義」と「実質含意のパラドクス」について。

（01）
（ⅰ）Ｐ→Ｑ├ ～Ｐ∨Ｑ
１　　（１）　　　　Ｐ→Ｑ　　　Ａ
　２　（２）　～（～Ｐ∨Ｑ）　　Ａ
　　３（３）　　　～Ｐ　　　　　Ａ
　　３（４）　　　～Ｐ∨Ｑ　　　３∨Ｉ
　２３（５）　～（～Ｐ∨Ｑ）＆
　　　　　　　　（～Ｐ∨Ｑ）　　２４＆Ｉ
　２　（６）　　～～Ｐ　　　　　３５ＲＡＡ
　２　（７）　　　　Ｐ　　　　　６ＤＮ
１２　（８）　　　　　　Ｑ　　　１７ＭＰＰ
１２　（９）　　　～Ｐ∨Ｑ　　　８∨Ｉ
１２　（ア）　～（～Ｐ∨Ｑ）＆
　　　　　　　　（～Ｐ∨Ｑ）　　２９＆Ｉ
１　　（イ）～～（～Ｐ∨Ｑ）　　２アＲＡＡ
１　　（ウ）　　　～Ｐ∨Ｑ　　　イＤＮ
（ⅱ）～Ｐ∨Ｑ├ Ｐ→Ｑ
１　　　　　（１）　～Ｐ∨　Ｑ　　　Ａ
　２　　　　（２）　　Ｐ＆～Ｑ　　　Ａ
　　３　　　（３）　～Ｐ　　　　　　Ａ
　２　　　　（４）　　Ｐ　　　　　　２＆Ｅ
　２３　　　（５）　～Ｐ＆　Ｐ　　　３４＆Ｉ
　　３　　　（６）～（Ｐ＆～Ｑ）　　２５ＲＡＡ
　　　７　　（７）　　　　　Ｑ　　　Ａ
　２　　　　（８）　　　　～Ｑ　　　Ａ
　２　７　　（９）　　Ｑ＆～Ｑ　　　７８＆Ｉ
　　　７　　（ア）～（Ｐ＆～Ｑ）　　２９ＲＡＡ
１　　　　　（イ）～（Ｐ＆～Ｑ）　　１３６７ア∨Ｅ
　　　　ウ　（ウ）　　Ｐ　　　　　　Ａ
　　　　　エ（エ）　　　　～Ｑ　　　Ａ
　　　　ウエ（オ）　　Ｐ＆～Ｑ　　　エオ＆Ｉ
１　　　ウエ（カ）～（Ｐ＆～Ｑ）＆
　　　　　　　　　　（Ｐ＆～Ｑ）　　イオ＆Ｉ
１　　　ウ　（キ）　　　～～Ｑ　　　７カＲＡＡ
１　　　ウ　（ク）　　　　　Ｑ　　　キＤＮ
１　　　　　（ケ）　　Ｐ→　Ｑ　　　ウクＣＰ
従って、
（01）により、
（02）
① 　Ｐ→Ｑ
② ～Ｐ∨Ｑ
に於いて、
①＝② は「含意の定義」である。
然るに、
（03）
① 　Ｐ→Ｑ
② ～Ｐ∨Ｑ
に於いて、
①＝② であるならば、
① 　偽→Ｑ
② ～偽∨Ｑ
に於いても、
①＝② である。
然るに、
（04）
～偽＝偽ではない＝真である＝真。
従って、
（03）（04）により、
（05）
② ～偽∨Ｑ
③ 　真∨Ｑ
に於いて、
②＝③ である。
従って、
（03）（05）により、
（06）
① 　偽→Ｑ
② ～偽∨Ｑ
③　 真∨Ｑ
に於いて、
①＝②＝③ である。
従って、
（06）により、
（07）
① 偽→Ｑ
③ 真∨Ｑ
に於いて、
①＝③ である。
然るに、
（08）
③ Ａ∨Ｑ＝（Ａが真）であるか、または、（Ｑが真である）。
の場合は、
③ Ａが「真」であれば、それだけで、「真」である。
従って、
（07）（08）により、
（09）
① 偽→Ｑ
③ 真∨Ｑ
に於いて、
①＝③ であって、尚且つ、
③ は、「真」である。
従って、
（09）により、
（10）
① 偽→Ｑ
③ 真∨Ｑ
に於いて、
③ だけでなく、
① も、「真」である。
従って、
（10）により、
（11）
① 偽→Ｑ
は、「真」である。
然るに、
（12）
（Ｐ＆～Ｐ）は「矛盾」であるが、
「矛盾」は、「偽（ウソ）」である。
従って、
（11）（12）により、
（13）
① 偽→Ｑ
は、「真」であるため、
①（Ｐ＆～Ｐ）→Ｑ
は、「恒に真（トートロジー）」である。
然るに、
（14）
１　　　　　　（１）　　　　Ｐ　　　　　　Ａ
１　　　　　　（２）　　　　Ｐ∨　Ｑ　　　１∨Ｉ
　２　　　　　（３）　　　～Ｐ＆～Ｑ　　　Ａ
　　４　　　　（４）　　　　Ｐ　　　　　　Ａ
　２　　　　　（５）　　　～Ｐ　　　　　　３＆Ｅ
　２４　　　　（６）　　　　Ｐ＆～Ｐ　　　４５＆Ｉ
　　４　　　　（７）　～（～Ｐ＆～Ｑ）　　２６ＲＡＡ
　　　８　　　（８）　　　　　　　Ｑ　　　Ａ
　２　　　　　（９）　　　　　　～Ｑ　　　３＆Ｅ
　２　８　　　（ア）　　　　Ｑ＆～Ｑ　　　８９＆Ｉ
　　　８　　　（イ）　～（～Ｐ＆～Ｑ）　　２アＲＡＡ
１　　　　　　（ウ）　～（～Ｐ＆～Ｑ）　　１４７８イ∨Ｅ
　　　　エ　　（エ）　　　～Ｐ　　　　　　Ａ
　　　　　オ　（オ）　　　　　　～Ｑ　　　Ａ
　　　　エオ　（カ）　　　～Ｐ＆～Ｑ　　　エオ＆Ｉ
１　　　エオ　（キ）　～（～Ｐ＆～Ｑ）＆
　　　　　　　　　　　　（～Ｐ＆～Ｑ）　　ウカ＆Ｉ
１　　　エ　　（ク）　　　　　～～Ｑ　　　オキＲＡＡ
１　　　エ　　（ケ）　　　　　　　Ｑ　　　エＤＮ
１　　　　　　（コ）　　　～Ｐ→　Ｑ　　　エケＣＰ
　　　　　　　（サ）　Ｐ→（～Ｐ→Ｑ）　　１コＣＰ
　　　　　　シ（シ）　Ｐ＆　～Ｐ　　　　　Ａ
　　　　　　シ（ス）　Ｐ　　　　　　　　　シ＆Ｅ
　　　　　　シ（セ）　　　　～Ｐ→Ｑ　　　サスＭＰＰ
　　　　　　シ（ソ）　　　　～Ｐ　　　　　シ＆Ｅ
　　　　　　シ（タ）　　　　　　　Ｑ　　　セソＭＰＰ
　　　　　　　（チ）（Ｐ＆～Ｐ）→Ｑ　　　シタＣＰ
従って、
（13）（14）により、
（15）
果たして、
①（Ｐ＆～Ｐ）→Ｑ
は、「恒に真（トートロジー）」である。
従って、
（01）～（15）により、
（16）
① 　Ｐ→Ｑ
② ～Ｐ∨Ｑ
に於いて、
①＝② である（含意の定義）。
といふ「結果」として、
①（Ｐ＆～Ｐ）→Ｑ
は、「恒に真（トートロジー）」である。
然るに、
（17）
① 　Ｐ→Ｑ
② ～Ｐ∨Ｑ
に於いて、
Ｐ＝～Ｐ
といふ「代入」を行ふと、
① 　～Ｐ→Ｑ
② ～～Ｐ∨Ｑ
従って、
（17）により、
（18）
「二重否定律（ＤＮ）」により、
① ～Ｐ→Ｑ
② 　Ｐ∨Ｑ
に於いて、すなはち、
① Ｐでないならば、　　Ｑである。
② Ｐであるか、または、Ｑである。
に於いて、
①＝② であるが、このことは、「当然」である。
従って、
（17）（18）により、
（19）
① Ｐでないならば、　　Ｑである。
② Ｐであるか、または、Ｑである。
に於いて、
①＝② である。
といふ「この点」からすれば、
① 　Ｐ→Ｑ
② ～Ｐ∨Ｑ
に於いて、
①＝② である。
といふことは、「むしろ、当然」である。
然るに、
（20）
「ウィキペディア（適切さの論理）」によると、
例えば以下の三つの条件文は全て古典論理においては真であるが、我々は真であるとは考えない。
「１＋１＝２」ならば「雪は白い」
「１＋１＝５」ならば「雪は白い」
「１＋１＝５」ならば「雪は黒い」
この我々が普段使用する「ならば」と古典論理における実質含意の乖離が実質含意のパラドクスである。
この我々が普段使用する「ならば」と実質含意の乖離について、多くの研究が行われきた（Anderson and Belnap 1975, Cheng 1996）。
との、ことである。
然るに、
（19）（20）により、
（21）
①「１＋１＝２」ならば「雪は白い」
②「１＋１＝５」ならば「雪は白い」
③「１＋１＝５」ならば「雪は黒い」
といふ「命題」は、「実質含意」としては、
①「１＋１≠２」であるか、または、「雪は白い」
②「１＋１≠５」であるか、または、「雪は白い」
③「１＋１≠５」であるか、または、「雪は黒い」
といふ「意味」である。
然るに、
（22）
④「１＋１≠２」であるか、または、「雪は黒い」
ではないため、
①「１＋１≠２」であるか、または、「雪は白い」
②「１＋１≠５」であるか、または、「雪は白い」
③「１＋１≠５」であるか、または、「雪は黒い」
といふ「命題」は、「３つ」とも、「真（本当）」である。
因みに、
（23）
六・一　論理学の命題はトートロジーである。
六・一一　論理学の命題は何ごとも語らない。（分析命題である。）
（吉田徹也、ウィトゲンシュタイン 論理哲学論考、2019年、２７８頁）
でいふ「論理学」は、
① 　Ｐ→Ｑ
② ～Ｐ∨Ｑ
に於いて、
①＝② である（含意の定義）。
やうな「（古典）論理学」を言ふ。
令和０４年１１月０９日、毛利太。

「（矛盾）が「真」ならば、（何でも有り）。」は「恒真（トートロジー）」である。

（01）
（ａ）
原始的規則あるいは導出された規則を、既に証明されたどのような連式あるいは定理とでもともに用いて、証明すると、
１　（１）　　　　Ｐ　　　　Ａ
１　（２）　　　　Ｐ∨Ｑ　　１∨Ｉ
１　（３）　　～～Ｐ∨Ｑ　　２ＤＮ
１　（４）　　　～Ｐ→Ｑ　　３含意の定義
　　（５）Ｐ→（～Ｐ→Ｑ）　１４ＣＰ
　６（６）Ｐ＆　～Ｐ　　　　Ａ
　６（７）Ｐ　　　　　　　　６＆Ｅ
　６（８）　　　～Ｐ→Ｑ　　５７ＭＰＰ
　６（９）　　　～Ｐ　　　　６＆Ｅ
　６（ア）　　　　　　Ｑ　　８９ＭＰＰ
　　（イ）　Ｐ＆～Ｐ→Ｑ　　６アＣＰ
（ｂ）
原始的規則だけを用いて、証明すると、
１　　　　　　（１）　　　Ｐ　　　　　　Ａ
１　　　　　　（２）　　　Ｐ∨　Ｑ　　　１∨Ｉ
　２　　　　　（３）　　～Ｐ＆～Ｑ　　　Ａ
　　４　　　　（４）　　　Ｐ　　　　　　Ａ
　２　　　　　（５）　　～Ｐ　　　　　　３＆Ｅ
　２４　　　　（６）　　　Ｐ＆～Ｐ　　　４５＆Ｉ
　　４　　　　（７）～（～Ｐ＆～Ｑ）　　２６ＲＡＡ
　　　８　　　（８）　　　　　　Ｑ　　　Ａ
　２　　　　　（９）　　　　　～Ｑ　　　３＆Ｅ
　２　８　　　（ア）　　　Ｑ＆～Ｑ　　　８９＆Ｉ
　　　８　　　（イ）～（～Ｐ＆～Ｑ）　　２アＲＡＡ
１　　　　　　（ウ）～（～Ｐ＆～Ｑ）　　１４７８イ∨Ｅ
　　　　エ　　（エ）　　～Ｐ　　　　　　Ａ
　　　　　オ　（オ）　　　　　～Ｑ　　　Ａ
　　　　エオ　（カ）　　～Ｐ＆～Ｑ　　　エオ＆Ｉ
１　　　エオ　（キ）～（～Ｐ＆～Ｑ）＆
　　　　　　　　　　　（～Ｐ＆～Ｑ）　　ウカ＆Ｉ
１　　　エ　　（ク）　　　　～～Ｑ　　　オキＲＡＡ
１　　　エ　　（ケ）　　　　　　Ｑ　　　エＤＮ
１　　　　　　（コ）　　～Ｐ→　Ｑ　　　エケＣＰ
　　　　　　　（サ）Ｐ→（～Ｐ→Ｑ）　　１コＣＰ
　　　　　　シ（シ）Ｐ＆　～Ｐ　　　　　Ａ
　　　　　　シ（ス）Ｐ　　　　　　　　　シ＆Ｅ
　　　　　　シ（セ）　　　～Ｐ→Ｑ　　　サスＭＰＰ
　　　　　　シ（ソ）　　　～Ｐ　　　　　シ＆Ｅ
　　　　　　シ（タ）　　　　　　Ｑ　　　セソＭＰＰ
　　　　　　　（チ）　Ｐ＆～Ｐ→Ｑ　　　シタＣＰ
従って、
（01）により、
（02）
① 矛盾（Ｐ＆～Ｐ）
② 任意の命題（Ｑ）
に於いて、
① が「真」であるならば、
② も「真」である。
然るに、
（03）
① 矛盾（Ｐ＆～Ｐ）
② 任意の命題（Ｑ）
に於いて、
① は、「恒に偽」であるため、
② の「真偽」は、「不明」である。
従って、
（03）により、
（04）
　Ｐ＝太陽は東から昇る。
～Ｐ＝太陽は西から昇る。
　Ｑ＝バカボンのパパは天才である。
であるとして、
① 太陽は東から昇って、太陽は西から昇る。
② バカボンのパパは天才である。
に於いて、
① ならば、② である。
といふ「仮言命題」は、「恒真（トートロジー）」であるが、
② が「真であるか、偽であるか」は、「不明」である。
令和０４年１１月０９日、毛利太。

「（Ｐ→Ｑ）∨（Ｑ→Ｒ）」は「トートロジー（恒真式）」である。

（01）
５　原始的規則あるいは導出された規則を、既に証明されたどのような連式あるいは定理とでもともに用いて、証明せよ。
５　Using primitive or derived rules, together with any sequents or theorems already proved, prove:
（ｂ）├（Ｐ→Ｑ）∨（Ｑ→Ｒ）
（〃）「（ＰならばＱである）か（ＱならばＲである）。」は「恒に真である」。
（E.J.レモン 著、論理学初歩、竹尾治一郎・浅野楢英 訳、1973年、８０頁改）
然るに、
（02）
（ｂ）
　　（１）　Ｑ∨～Ｑ　　　　　　　Ａ（排中律）
２　（２）　Ｑ　　　　　　　　　　Ａ
２　（３）～Ｐ∨Ｑ　　　　　　　　２∨Ｉ
２　（４）　Ｐ→Ｑ　　　　　　　　３含意の定義
２　（５）（Ｐ→Ｑ）∨（Ｑ→Ｒ）　４∨Ｉ
　６（６）～Ｑ　　　　　　　　　　Ａ
　６（７）～Ｑ∨Ｒ　　　　　　　　６∨Ｉ
　６（８）　Ｑ→Ｒ　　　　　　　　７含意の定義
　６（９）（Ｐ→Ｑ）∨（Ｑ→Ｒ）　８∨Ｉ
　　（ア）（Ｐ→Ｑ）∨（Ｑ→Ｒ）　２５６９ＥＥ
（03）
５　原始的規則（10 primitive rules）だけを用いて、証明せよ。
（ｂ） ├（Ｐ→Ｑ）∨（Ｑ→Ｒ）
（E.J.レモン 著、論理学初歩、竹尾治一郎・浅野楢英 訳、1973年、８０頁改）
（04）
１　　　　　　　　　　　　　　（１）　～（Ｑ∨～Ｑ）　　　　Ａ
　２　　　　　　　　　　　　　（２）　　　Ｑ　　　　　　　　Ａ
　２　　　　　　　　　　　　　（３）　　　Ｑ∨～Ｑ　　　　　２∨Ｉ
１２　　　　　　　　　　　　　（４）　～（Ｑ∨～Ｑ）＆
　　　　　　　　　　　　　　　　　　　　（Ｑ∨～Ｑ）　　　　１３＆Ｉ
１　　　　　　　　　　　　　　（５）　　～Ｑ　　　　　　　　２４ＲＡＡ
１　　　　　　　　　　　　　　（６）　　　Ｑ∨～Ｑ　　　　　５∨Ｉ
１　　　　　　　　　　　　　　（７）　～（Ｑ∨～Ｑ）＆
　　　　　　　　　　　　　　　　　　　　（Ｑ∨～Ｑ）　　　　１６＆Ｉ
　　　　　　　　　　　　　　　（８）～～（Ｑ∨～Ｑ）　　　　１７ＲＡＡ
　　　　　　　　　　　　　　　（９）　　　Ｑ∨～Ｑ　　　　　８ＤＮ
　　　ア　　　　　　　　　　　（ア）　　　Ｑ　　　　　　　　Ａ（排中律・左項）
　　　ア　　　　　　　　　　　（イ）　　～Ｐ∨　Ｑ　　　　　ア∨Ｉ
　　　　ウ　　　　　　　　　　（ウ）　　　Ｐ＆～Ｑ　　　　　Ａ
　　　　　エ　　　　　　　　　（エ）　　～Ｐ　　　　　　　　Ａ
　　　　ウ　　　　　　　　　　（オ）　　　Ｐ　　　　　　　　ウ＆Ｅ
　　　　ウエ　　　　　　　　　（カ）　　～Ｐ＆Ｐ　　　　　　エオ＆Ｉ
　　　　　エ　　　　　　　　　（キ）　～（Ｐ＆～Ｑ）　　　　ウカＲＡＡ
　　　　　　ク　　　　　　　　（ク）　　　　　　Ｑ　　　　　Ａ
　　　　ウ　　　　　　　　　　（ケ）　　　　　～Ｑ　　　　　ウ＆Ｅ
　　　　ウ　ク　　　　　　　　（コ）　　　Ｑ＆～Ｑ　　　　　クケ＆Ｉ
　　　　　　ク　　　　　　　　（サ）　～（Ｐ＆～Ｑ）　　　　ウコＲＡＡ
　　　ア　　　　　　　　　　　（シ）　～（Ｐ＆～Ｑ）　　　　イエキクサ∨Ｅ
　　　　　　　ス　　　　　　　（ス）　　　Ｐ　　　　　　　　Ａ
　　　　　　　　セ　　　　　　（セ）　　　　　～Ｑ　　　　　Ａ
　　　　　　　スセ　　　　　　（ソ）　　　Ｐ＆～Ｑ　　　　　チツ＆Ｉ
　　　ア　　　スセ　　　　　　（タ）　～（Ｐ＆～Ｑ）＆
　　　　　　　　　　　　　　　　　　　　（Ｐ＆～Ｑ）　　　　キソ＆Ｉ
　　　ア　　　ス　　　　　　　（チ）　　　　～～Ｑ　　　　　セタＲＡＡ
　　　ア　　　ス　　　　　　　（ツ）　　　　　　Ｑ　　　　　チＤＮ
　　　ア　　　　　　　　　　　（テ）　　　Ｐ→　Ｑ　　　　　スツＣＰ
　　　ア　　　　　　　　　　　（ト）（Ｐ→Ｑ）∨（Ｑ→Ｒ）　テ∨Ｉ
　　　　　　　　　ナ　　　　　（ナ）　　　　　～Ｑ　　　　　Ａ（排中律・右項）
　　　　　　　　　ナ　　　　　（ニ）　　　　　～Ｑ∨Ｒ　　　ナ∨Ｉ
　　　　　　　　　　ヌ　　　　（ヌ）　　　　　Ｑ＆～Ｒ　　　Ａ
　　　　　　　　　　　ネ　　　（ネ）　　　　　～Ｑ　　　　　Ａ
　　　　　　　　　　ヌ　　　　（ノ）　　　　　Ｑ　　　　　　ヌ＆Ｅ
　　　　　　　　　　ヌネ　　　（ハ）　　　　　～Ｑ＆Ｑ　　　ネノ＆Ｉ
　　　　　　　　　　　ネ　　　（ヒ）　　　～（Ｑ＆～Ｒ）　　ヌハＲＡＡ
　　　　　　　　　　　　フ　　（フ）　　　　　　　　Ｒ　　　Ａ
　　　　　　　　　　ヌ　　　　（ヘ）　　　　　　　～Ｒ　　　ヌ＆Ｅ
　　　　　　　　　　ヌ　フ　　（ホ）　　　　　Ｒ＆～Ｒ　　　フヘ＆Ｉ
　　　　　　　　　　　　フ　　（マ）　　　～（Ｑ＆～Ｒ）　　ヌホＲＡＡ
　　　　　　　　　ナ　　　　　（ミ）　　　～（Ｑ＆～Ｒ）　　ニネヒフマ∨Ｅ
　　　　　　　　　　　　　ム　（ム）　　　　　Ｑ　　　　　　Ａ
　　　　　　　　　　　　　　メ（メ）　　　　　　　～Ｒ　　　Ａ
　　　　　　　　　　　　　ムメ（モ）　　　　　Ｑ＆～Ｒ　　　ムメ＆Ｉ
　　　　　　　　　ナ　　　ムメ（ヤ）　　　～（Ｑ＆～Ｒ）＆
　　　　　　　　　　　　　　　　　　　　　　（Ｑ＆～Ｒ）　　ミモ＆Ｉ
　　　　　　　　　ナ　　　ム　（い）　　　　　　～～Ｒ　　　メＲＡＡ
　　　　　　　　　ナ　　　ム　（ユ）　　　　　　　　Ｒ　　　いＤＮ
　　　　　　　　　ナ　　　　　（え）　　　　　Ｑ→　Ｒ　　　ムユＣＰ
　　　　　　　　　ナ　　　　　（ヨ）（Ｐ→Ｑ）∨（Ｑ→Ｒ）　え∨Ｉ
　　　　　　　　　　　　　　　（ラ）（Ｐ→Ｑ）∨（Ｑ→Ｒ）　９アトナヨ∨Ｅ
従って、
（02）（04）により、
（05）
いづれにせよ、
（ａ）├ 　　 Ｑ　∨～Ｑ
（ｂ）├（Ｐ→Ｑ）∨（Ｑ→Ｒ）
に於いて、
（ａ）が「恒真（トートロジー）」であるが故に、
（ｂ）も「恒真（トートロジー）」である。
然るに、
（06）
①（１→０）∨（０→Ｒ）≡０∨１≡１
②（Ｐ→１）∨（１→０）≡１∨０≡１
従って、
（05）（06）により、
（07）
（ｂ）├（Ｐ→Ｑ）∨（Ｑ→Ｒ）
は、確かに、「恒真（トートロジー）」である。
従って、
（06）（07）により、
（08）
（α）（Ａが日本人であるならば、Ａは男性である）。
（β）（Ａが男性であるならば、　Ａは家にゐる）。
に於いて、
（α）が「偽（ウソ）」ならば、
（β）は「真（本当）」であり、
（β）が「偽（ウソ）」であるならば、
（α）は「真（本当）」である。
令和０４年１１月０８日、毛利太。

「パースの法則」について。

（01）

然るに、
（02）
５　原始的規則あるいは導出された規則を、既に証明されたどのような連式あるいは定理とでもともに用いて、証明せよ。
（ｃ）├（（Ｐ→　Ｑ）→Ｐ）→Ｐ
（〃）├（（Ｐ→～Ｑ）→Ｐ）→Ｐ
（〃）├（（Ｐ→～Ｐ）→Ｐ）→Ｐ
（E.J.レモン 著、論理学初歩、竹尾治一郎・浅野楢英 訳、1973年、８０頁改）
然るに、
（03）
（ⅰ）
１　　（１）　　　　（Ｐ→Ｑ）→Ｐ　Ａ
１　　（２）　　　～（Ｐ→Ｑ）∨Ｐ　１含意の定義
　３　（３）　　　～（Ｐ→Ｑ）　　　Ａ
　３　（４）　　～（～Ｐ∨Ｑ）　　　Ａ
　３　（５）　　　　Ｐ＆～Ｑ　　　　４ド・モルガンの法則
　３　（６）　　　　Ｐ　　　　　　　５＆Ｅ
　　７（７）　　　　　　　　　　Ｐ　Ａ
１　　（８）　　　　　　　　　　Ｐ　１３６７７∨Ｅ
　　　（９）（（Ｐ→Ｑ）→Ｐ）→Ｐ　１８ＣＰ
（ⅱ）
１　　（１）　　　　（Ｐ→～Ｑ）→Ｐ　Ａ
１　　（２）　　　～（Ｐ→～Ｑ）∨Ｐ　１含意の定義
　３　（３）　　　～（Ｐ→～Ｑ）　　　Ａ
　３　（４）　　～（～Ｐ∨～Ｑ）　　　Ａ
　３　（５）　　　　Ｐ＆　　Ｑ　　　　４ド・モルガンの法則
　３　（６）　　　　Ｐ　　　　　　　　５＆Ｅ
　　７（７）　　　　　　　　　　　Ｐ　Ａ
１　　（８）　　　　　　　　　　　Ｐ　１３６７７∨Ｅ
　　　（９）（（Ｐ→～Ｐ）→Ｐ）→Ｐ　１８ＣＰ
（ⅲ）
１　　（１）　　　　（Ｐ→～Ｐ）→Ｐ　Ａ
１　　（２）　　　～（Ｐ→～Ｐ）∨Ｐ　１含意の定義
　３　（３）　　　～（Ｐ→～Ｐ）　　　Ａ
　３　（４）　　～（～Ｐ∨～Ｐ）　　　Ａ
　３　（５）　　　　Ｐ＆　　Ｐ　　　　４ド・モルガンの法則
　３　（６）　　　　Ｐ　　　　　　　　５＆Ｅ
　　７（７）　　　　　　　　　　　Ｐ　Ａ
１　　（８）　　　　　　　　　　　Ｐ　１３６７７∨Ｅ
　　　（９）（（Ｐ→～Ｐ）→Ｐ）→Ｐ　１８ＣＰ
従って、
（02）（03）により、
（04）
①├ （（Ｐ→　Ｑ）→Ｐ）→Ｐ
②├ （（Ｐ→～Ｑ）→Ｐ）→Ｐ
③├ （（Ｐ→～Ｐ）→Ｐ）→Ｐ
といふ「論理式（パースの法則）」すなはち、
①├ （（ＰならばＱである）ならばＰ）ならばＰである
②├ （（ＰならばＱでない）ならばＰ）ならばＰである。
③├ （（ＰならばＰでない）ならばＰ）ならばＰである。
といふ「パースの法則」は、３つとも、「トートロジー（恒真式）」である。
従って、
（01）（04）により、
（05）
命題計算では、パースの法則は ((P→Q)→P)→P のことを言う。この意味するところを書き出すと、命題Pについて、命題Qが存在して、「PならばQ」からPが真であることが従うときには、Pは真でなければならないとなる。とりわけ、Qとして偽を選んだ場合には、Pから偽が従うときは常にPが真であるならば、Pは真であるとなる（ウィキペディア）。
といふ『わけ』ではない。
令和０４年１１月０７日、毛利太。

「兎は耳が長い」の「述語論理（Ⅰ・Ⅱ）」。

（01）
（Ⅰ）
１　　　　　（１）∀ｘ｛象ｘ→∃ｙ（鼻ｙｘ＆長ｙ）＆∀ｚ（～鼻ｚｘ→～長ｚ）｝　Ａ
　２　　　　（２）∀ｘ｛兎ｘ→∃ｙ（長ｙ＆耳ｙｘ）＆∀ｚ（耳ｚｘ→～鼻ｚｘ）｝　Ａ
　　３　　　（３）∃ｘ（兎ｘ＆象ｘ）　　　　　　　　　　　　　　　　　　　　　　Ａ
１　　　　　（４）　　　象ａ→∃ｙ（鼻ｙａ＆長ｙ）＆∀ｚ（～鼻ｚａ→～長ｚ）　　１ＵＥ
　２　　　　（５）　　　兎ａ→∃ｙ（長ｙ＆耳ｙａ）＆∀ｚ（耳ｚａ→～鼻ｚａ）　　２ＵＥ
　　　６　　（６）　　　兎ａ＆象ａ　　　　　　　　　　　　　　　　　　　　　　　Ａ
　　　６　　（７）　　　兎ａ　　　　　　　　　　　　　　　　　　　　　　　　　　６＆Ｅ
　　　６　　（８）　　　　　　象ａ　　　　　　　　　　　　　　　　　　　　　　　６＆Ｅ
１　　６　　（９）　　　　　　∃ｙ（鼻ｙａ＆長ｙ）＆∀ｚ（～鼻ｚａ→～長ｚ）　　４８ＭＰＰ
　２　６　　（ア）　　　　　　∃ｙ（長ｙ＆耳ｙａ）＆∀ｚ（耳ｚａ→～鼻ｚａ）　　５７ＭＰＰ
１　　６　　（イ）　　　　　　∃ｙ（鼻ｙａ＆長ｙ）　　　　　　　　　　　　　　　９＆Ｅ
　　　　ウ　（ウ）　　　　　　　　　鼻ｂａ＆長ｂ　　　　　　　　　　　　　　　　Ａ
　２　６　　（エ）　　　　　　∃ｙ（長ｙ＆耳ｙａ）　　　　　　　　　　　　　　　ア＆Ｅ
　　　　　オ（オ）　　　　　　　　　長ｂ＆耳ｂａ　　　　　　　　　　　　　　　　Ａ
　　　　　オ（カ）　　　　　　　　　　　　耳ｂａ　　　　　　　　　　　　　　　　オ＆Ｅ
１　　６　　（キ）　　　　　　　　　　　　　　　　　∀ｚ（～鼻ｚａ→～長ｚ）　　９＆Ｅ
　２　６　　（ク）　　　　　　　　　　　　　　　　　∀ｚ（耳ｚａ→～鼻ｚａ）　　ア＆Ｅ
１　　６　　（ケ）　　　　　　　　　　　　　　　　　　　　～鼻ｂａ→～長ｂ　　　キＵＥ
　２　６　　（コ）　　　　　　　　　　　　　　　　　　　　耳ｂａ→～鼻ｂａ　　　クＵＥ
　２　６　オ（サ）　　　　　　　　　　　　　　　　　　　　　　　　～鼻ｂａ　　　カコＭＰＰ
１２　６　オ（シ）　　　　　　　　　　　　　　　　　　　　　　　　　～長ｂ　　　ケサＭＰＰ
　　　　　オ（ス）　　　　　　　　　長ｂ　　　　　　　　　　　　　　　　　　　　オ＆Ｅ
１２　６　オ（セ）　　　　　　　　　長ｂ＆～長ｂ　　　　　　　　　　　　　　　　シス＆Ｉ
１２　６　　（ソ）　　　　　　　　　長ｂ＆～長ｂ　　　　　　　　　　　　　　　　エオセＥＥ
１２３　　　（タ）　　　　　　　　　長ｂ＆～長ｂ　　　　　　　　　　　　　　　　３６ソＥＥ
１２　　　　（チ）～∃ｘ（兎ｘ＆象ｘ）　　　　　　　　　　　　　　　　　　　　　３タＲＡＡ
１２　　　　（ツ）∀ｘ～（兎ｘ＆象ｘ）　　　　　　　　　　　　　　　　　　　　　チ量化子の関係
１２　　　　（テ）　　～（兎ａ＆象ａ）　　　　　　　　　　　　　　　　　　　　　ツＵＥ
１２　　　　（ト）　　～兎ａ∨～象ａ　　　　　　　　　　　　　　　　　　　　　　テ、ド・モルガンの法則
１２　　　　（ナ）　　　兎ａ→～象ａ　　　　　　　　　　　　　　　　　　　　　　ト含意の定義
１２　　　　（ニ）∀ｘ（兎ｘ→～象ｘ）　　　　　　　　　　　　　　　　　　　　　ナＵＩ
然るに、
（02）
（Ⅱ）
１　　　（１）∀ｘ｛象ｘ→∃ｙ（鼻ｙｘ＆長ｙ）＆∀ｚ（～鼻ｚｘ→～長ｚ）｝　　Ａ
　２　　（２）∀ｘ｛兎ｘ→∃ｚ（耳ｚｘ＆～鼻ｚｘ＆長ｚ）｝　　　　　　　　　　Ａ
１　　　（３）　　　象ａ→∃ｙ（鼻ｙａ＆長ｙ）＆∀ｚ（～鼻ｚａ→～長ｚ）　　　１ＵＥ
　２　　（４）　　　兎ａ→∃ｚ（耳ｚａ＆～鼻ｚａ＆長ｚ）　　　　　　　　　　　２ＵＥ
　　５　（５）　　　兎ａ　　　　　　　　　　　　　　　　　　　　　　　　　　　Ａ
　２５　（６）　　　　　　∃ｚ（耳ｚａ＆～鼻ｚａ＆長ｚ）　　　　　　　　　　　４５ＭＰＰ
　　　７（７）　　　　　　　　　耳ｂａ＆～鼻ｂａ＆長ｂ　　　　　　　　　　　　Ａ
　　　７（８）　　　　　　　　　　　　　～鼻ｂａ＆長ｂ　　　　　　　　　　　　７＆Ｅ
　　　７（９）　　　　　　　　　　　～（鼻ｂａ∨～長ｂ）　　　　　　　　　　　８ド・モルガンの法則
　　　７（ア）　　　　　　　　　　～（～鼻ｂａ→～長ｂ）　　　　　　　　　　　９含意の定義
　　　７（イ）　　　　　　　　∃ｚ～（～鼻ｚａ→～長ｚ）　　　　　　　　　　　アＥＩ
　２５　（ウ）　　　　　　　　∃ｚ～（～鼻ｚａ→～長ｚ）　　　　　　　　　　　６７イＥＥ
　２５　（エ）　　　　　　　　～∀ｚ（～鼻ｚａ→～長ｚ）　　　　　　　　　　　ウ量化子の関係
　２５　（オ）　　　　　～∃ｙ（鼻ｙａ＆長ｙ）∨～∀ｚ（～鼻ｚａ→～長ｚ）　　エ∨Ｉ
　２５　（カ）　　　　～｛∃ｙ（鼻ｙａ＆長ｙ）＆　∀ｚ（～鼻ｚａ→～長ｚ）｝　オ、ド・モルガンの法則
１２５　（キ）　　～象ａ　　　　　　　　　　　　　　　　　　　　　　　　　　　３カＭＴＴ
１２　　（ク）　　　兎ａ→～象ａ　　　　　　　　　　　　　　　　　　　　　　　５キＣＰ
１２　　（ケ）∀ｘ（兎ｘ→～象ｘ）　　　　　　　　　　　　　　　　　　　　　　クＵＩ
従って、
（01）（02）により、
（03）
① ∀ｘ｛兎ｘ→∃ｙ（長ｙ＆耳ｙｘ）＆∀ｚ（耳ｚｘ→～鼻ｚｘ）｝。
② ∀ｘ｛兎ｘ→∃ｚ（耳ｚｘ＆～鼻ｚｘ＆長ｚ）｝。
であるならば、すなはち、
① すべてのｘについて｛ｘが兎であるならば、あるｙは（長くて、ｘの耳であり）、すべてのｚについて（ｚがｘの耳であるならば、ｚはｘの鼻ではない）｝。
② すべてのｘについて｛ｘが兎であるならば、あるｚは（ｘの耳であって、ｘの鼻ではなく、ｚは長い）｝。
であるならば、
① よりも、
② の方が、「簡単で、分かりやすい」。
（04）
「命題計算」の「練習問題」を解いてたためか、
（ⅰ）　　∃ｚ（耳ｚａ＆～鼻ｚａ＆長ｚ）
（ⅱ）～｛∃ｙ（鼻ｙａ＆長ｙ）＆∀ｚ（～鼻ｚａ→～長ｚ）｝
に於いて、
（ⅰ）からは、
（ⅱ）が得られる。
といふことに「気付くこと」が出来、それならば、
① ∀ｘ｛兎ｘ→∃ｙ（長ｙ＆耳ｙｘ）＆∀ｚ（耳ｚｘ→～鼻ｚｘ）｝
② ∀ｘ｛兎ｘ→∃ｚ（耳ｚｘ＆～鼻ｚｘ＆長ｚ）｝
に於いて、
① でなくとも、
② で「十分」であると思ひ立って、
（Ⅰ）を、（Ⅱ）に「書き直した」。
といふ「次第」である。
（05）
（ⅰ）∀ｘ｛象ｘ→∃ｙ（鼻ｙｘ＆長ｙ）＆∀ｚ（～鼻ｚｘ→～長ｚ）｝。然るに、
（ⅱ）∀ｘ｛兎ｘ→∃ｚ（耳ｚｘ＆～鼻ｚｘ＆長ｚ）｝。従って、
（ⅲ）∀ｘ（兎ｘ→～象ｘ）。
といふ「推論（三段論法）」、すなわち、
（ⅰ）すべてのｘについて｛ｘが象であるならば、あるｙは（ｘの鼻であって、長く）、すべてのｚについて（ｚがｘの鼻でないならば、ｚは長くない）｝。然るに、
（ⅱ）すべてのｘについて｛ｘが兎であるならば、あるｚは（ｘの耳であって、ｘの鼻ではなく、ｚは長い）｝。従って、
（ⅲ）すべてのｘについて（ｘが兎ならば、ｘは象ではない）。
といふ「推論」、すなはち、
（ⅰ）象は鼻が長い。然るに、
（ⅱ）兎の耳は長いが、耳は鼻ではない。従って、
（ⅲ）兎は象ではない。
といふ「推論（三段論法）」は、「妥当」である。
然るに、
（06）
（ⅰ）象は、鼻と耳が長い。然るに、
（ⅱ）ピーターの耳は長いが、耳は鼻ではない。従って、
（ⅲ）ピーターは象ではない。
といふ「推論（三段論法）」は、「妥当」ではない。
然るに、
（07）
（ⅰ）象は、鼻は長く、鼻以外は長くない。然るに、
（ⅱ）ピーターの耳は長いが、耳は鼻ではない。従って、
（ⅲ）ピーターは象ではない。
といふ「推論（三段論法）」は、「妥当」である。
従って、
（05）（06）（07）により、
（08）
① 象は、鼻が長い。
② 象は、鼻は長く、鼻以外は長くない。
③ 象は、鼻は長く、鼻以外も長い。
に於いて、
①＝② であって、
①＝③ ではない。
令和４年１１月０６日、毛利太。

「象は鼻が長い（三上文法）」は「（論理学としては）役に立たない」。

（01）
「（ブログ開設当初からの）これまでの三段論法」である、
（ⅰ）∀ｘ｛象ｘ→∃ｙ（鼻ｙｘ＆長ｙ）＆∀ｚ（～鼻ｚｘ→～長ｚ）｝。然るに、
（ⅱ）∀ｘ｛兎ｘ→∃ｙ（長ｙ＆耳ｙｘ）＆∀ｚ（耳ｚｘ→～鼻ｚｘ）｝。従って、
（ⅲ）∀ｘ（兎ｘ→～象ｘ）。
とは「異なる三段論法」を書くことにする。
（02）
１　　　（１）∀ｘ｛象ｘ→∃ｙ（鼻ｙｘ＆長ｙ）＆∀ｚ（～鼻ｚｘ→～長ｚ）｝　　Ａ
　２　　（２）∀ｘ｛兎ｘ→∃ｚ（耳ｚｘ＆～鼻ｚｘ＆長ｚ）｝　　　　　　　　　　Ａ
１　　　（３）　　　象ａ→∃ｙ（鼻ｙａ＆長ｙ）＆∀ｚ（～鼻ｚａ→～長ｚ）　　　１ＵＥ
　２　　（４）　　　兎ａ→∃ｚ（耳ｚａ＆～鼻ｚａ＆長ｚ）　　　　　　　　　　　２ＵＥ
　　５　（５）　　　兎ａ　　　　　　　　　　　　　　　　　　　　　　　　　　　Ａ
　２５　（６）　　　　　　∃ｚ（耳ｚａ＆～鼻ｚａ＆長ｚ）　　　　　　　　　　　４５ＭＰＰ
　　　７（７）　　　　　　　　　耳ｂａ＆～鼻ｂａ＆長ｂ　　　　　　　　　　　　Ａ
　　　７（８）　　　　　　　　　　　　　～鼻ｂａ＆長ｂ　　　　　　　　　　　　７＆Ｅ
　　　７（９）　　　　　　　　　　　～（鼻ｂａ∨～長ｂ）　　　　　　　　　　　８ド・モルガンの法則
　　　７（ア）　　　　　　　　　　～（～鼻ｂａ→～長ｂ）　　　　　　　　　　　９含意の定義
　　　７（イ）　　　　　　　　∃ｚ～（～鼻ｚａ→～長ｚ）　　　　　　　　　　　アＥＩ
　２５　（ウ）　　　　　　　　∃ｚ～（～鼻ｚａ→～長ｚ）　　　　　　　　　　　６７イＥＥ
　２５　（エ）　　　　　　　　～∀ｚ（～鼻ｚａ→～長ｚ）　　　　　　　　　　　ウ量化子の関係
　２５　（オ）　　　　　～∃ｙ（鼻ｙａ＆長ｙ）∨～∀ｚ（～鼻ｚａ→～長ｚ）　　エ∨Ｉ
　２５　（カ）　　　　～｛∃ｙ（鼻ｙａ＆長ｙ）＆　∀ｚ（～鼻ｚａ→～長ｚ）｝　オ、ド・モルガンの法則
１２５　（キ）　　～象ａ　　　　　　　　　　　　　　　　　　　　　　　　　　　３カＭＴＴ
１２　　（ク）　　　兎ａ→～象ａ　　　　　　　　　　　　　　　　　　　　　　　５キＣＰ
１２　　（ケ）∀ｘ（兎ｘ→～象ｘ）　　　　　　　　　　　　　　　　　　　　　　クＵＩ
従って、
（02）により、
（03）
（ⅰ）∀ｘ｛象ｘ→∃ｙ（鼻ｙｘ＆長ｙ）＆∀ｚ（～鼻ｚｘ→～長ｚ）｝。然るに、
（ⅱ）∀ｘ｛兎ｘ→∃ｚ（耳ｚｘ＆～鼻ｚｘ＆長ｚ）｝。従って、
（ⅲ）∀ｘ（兎ｘ→～象ｘ）。
といふ「推論」、すなわち、
（ⅰ）すべてのｘについて｛ｘが象であるならば、あるｙは（ｘの鼻であって、長く）、すべてのｚについて（ｚがｘの鼻でないならば、ｚは長くない）｝。然るに、
（ⅱ）すべてのｘについて｛ｘが兎であるならば、あるｚは（ｘの耳であって、ｘの鼻ではなく、ｚは長い）｝。従って、
（ⅲ）すべてのｘについて（ｘが兎ならば、ｘは象ではない）。
といふ「推論」は「妥当」である。
従って、
（03）により、
（04）
（ⅰ）象は鼻が長い。　　　　　　　然るに、
（ⅱ）兎の耳は鼻ではないが、長い。従って、
（ⅲ）兎は象ではない。
といふ「推論」は、「述語論理」としても「妥当」である。
従って、
（02）（03）（04）により、
（05）
「換言」すると、
① 象は鼻が長い。
② ∀ｘ｛象ｘ→∃ｙ（鼻ｙｘ＆長ｙ）＆∀ｚ（～鼻ｚｘ→～長ｚ）｝。
に於いて、
①＝② でなければ、
（ⅰ）象は鼻が長い。　　　　　　　然るに、
（ⅱ）兎の耳は鼻ではないが、長い。従って、
（ⅲ）兎は象ではない。
といふ「推論」は、「妥当」ではない。
然るに、
（06）
「象は鼻が長い」はどれが主辞がわからないから、このままでは非論理的な構造の文である、と言う人がもしあった（沢田『入門』二九ペ）とすれば、その人は旧『論理学』を知らない人であろう、これはこのままで、
　象は　鼻が長い。
　主辞　賓辞
とはっきりしている。速水式に簡単明リョウである。意味も、主辞賓辞の関係も小学生にもわかるはずの文である。これに文句をつけたり、それを取り次いだりするのは、人々が西洋文法に巻かれていることを語る以外の何物でもない。このまま定理扱いしてもよろしい。そしてこの定理の逆は真でないとして、鼻の長いもの例に、鞍馬山の天狗だの、池の尾の禅珍内供だのを上げるのも一興だろう。それでおしまいである（三上章、日本語の論理、1963年、１３・１４頁）。
従って、

（06）により、
（07）
「三上文法」に於いては、
① 象は鼻が長い。
② ∀ｘ｛象ｘ→∃ｙ（鼻ｙｘ＆長ｙ）＆∀ｚ（～鼻ｚｘ→～長ｚ）｝。
に於いて、
①＝② ではない。
従って、
（07）により、
（08）
「三上章、日本語の論理、1963年」は、
① 象は鼻が長い。⇔
② ∀ｘ｛象ｘ→∃ｙ（鼻ｙｘ＆長ｙ）＆∀ｚ（～鼻ｚｘ→～長ｚ）｝。
といふ「日本語」を、「論理的に、分析をしてゐる」といふわけではない。
令和４年１１月０６日、毛利太。

「ド・モルガンの法則」としての「量化子の関係」。

（01）
（ⅰ）
１　　　（１）　～（　Ｐ∨　Ｑ）　　Ａ
　２　　（２）　～（～Ｐ＆～Ｑ）　　Ａ
　　３　（３）　　　　Ｐ　　　　　　Ａ
　　３　（４）　　　　Ｐ∨　Ｑ　　　３∨Ｉ
１　３　（５）　～（　Ｐ∨　Ｑ）＆
　　　　　　　　　（　Ｐ∨　Ｑ）　　１４＆Ｉ
１　　　（６）　　　～Ｐ　　　　　　３５ＲＡＡ
　　　７（７）　　　　　　　Ｑ　　　Ａ
　　　７（８）　　　　Ｐ∨　Ｑ　　　７∨Ｉ
１　　７（９）　～（　Ｐ∨　Ｑ）＆
　　　　　　　　　（　Ｐ∨　Ｑ）　　１８＆Ｉ
１　　　（ア）　　　　　　～Ｑ　　　７９ＲＡＡ
１　　　（イ）　　　～Ｐ＆～Ｑ　　　６ア＆Ｉ
１２　　（ウ）　～（～Ｐ＆～Ｑ）＆
　　　　　　　　　（～Ｐ＆～Ｑ）　　２イ＆Ｉ
１　　　（エ）～～（～Ｐ＆～Ｑ）　　２ウＲＡＡ
１　　　（オ）　　　～Ｐ＆～Ｑ　　　エＤＮ
（ⅱ）
１　　　（１）　　　～Ｐ＆～Ｑ　　　Ａ
　２　　（２）　　　　Ｐ∨　Ｑ　　　Ａ
１　　　（３）　　　～Ｐ　　　　　　１＆Ｅ
　　４　（４）　　　　Ｐ　　　　　　Ａ
１　４　（５）　　　～Ｐ＆Ｐ　　　　３４＆Ｉ
　　４　（６）　～（～Ｐ＆～Ｑ）　　１５ＲＡＡ
１　　　（７）　　　　　　～Ｑ　　　１＆Ｅ
　　　８（８）　　　　　　　Ｑ　　　Ａ
１　　８（９）　　　　～Ｑ＆Ｑ　　　７８＆Ｉ
　　　８（ア）　～（～Ｐ＆～Ｑ）　　１９ＲＡＡ
　２　　（イ）　～（～Ｐ＆～Ｑ）　　２４６８ア∨Ｅ
１２　　（ウ）　　（～Ｐ＆～Ｑ）＆
　　　　　　　　～（～Ｐ＆～Ｑ）　　１ウ＆Ｉ
１　　　（エ）　　～（Ｐ∨　Ｑ）　　２ウＲＡＡ
従って、
（01）により、
（02）
① ～（Ｐ∨　Ｑ）
②　 ～Ｐ＆～Ｑ
に於いて、
①＝② は「ド・モルガンの法則」である。
従って、
（02）により、
（03）
① ～（Ｐ∨　Ｑ）
②　 ～Ｐ＆～Ｑ
に於いて、
Ｐ＝（Ｐ∨Ｑ）
Ｑ＝（Ｒ∨Ｓ）
といふ「代入」を行ふと、
① ～（Ｐ∨Ｑ ∨ Ｒ∨Ｓ）
② ～（Ｐ∨Ｑ）＆～（Ｒ∨Ｓ）
に於いて、
①＝② は「ド・モルガンの法則」である。
然るに、
（04）
（ⅱ）
１（１）～（Ｐ∨Ｑ）＆～（Ｒ∨Ｓ）　Ａ
１（２）～（Ｐ∨Ｑ）　　　　　　　　１＆Ｅ
１（３）～Ｐ＆～Ｑ　　　　　　　　　２ド・モルガンの法則
１（４）　　　　　　　～（Ｒ∨Ｓ）　１＆Ｅ
１（５）　　　　　　　～Ｒ＆～Ｓ　　４ド・モルガンの法則
１（６）～Ｐ＆～Ｑ　＆～Ｒ＆～Ｓ　　３５＆Ｉ
（ⅲ）
１（１）～Ｐ＆～Ｑ　＆～Ｒ＆～Ｓ　　Ａ
１（２）～Ｐ＆～Ｑ　　　　　　　　　１＆Ｅ
１（３）～（Ｐ∨Ｑ）　　　　　　　　２ド・モルガンの法則
１（４）　　　　　　　～Ｒ＆～Ｓ　　１＆Ｅ
１（５）　　　　　　　～（Ｒ∨Ｓ）　４ド・モルガンの法則
４（６）～（Ｐ∨Ｑ）＆～（Ｒ∨Ｓ）　３５＆Ｉ
従って、
（05）
② ～（Ｐ∨Ｑ）＆～（Ｒ∨Ｓ）
③ ～Ｐ＆～Ｑ　＆～Ｒ＆～Ｓ
に於いて、
②＝③ は「ド・モルガンの法則」である。
従って、
（03）（05）により、
（06）
① ～（Ｐ∨Ｑ ∨     Ｒ∨Ｓ）
② ～（Ｐ∨Ｑ）＆～（Ｒ∨Ｓ）
③ ～Ｐ＆～Ｑ　＆～Ｒ＆～Ｓ
に於いて、
①＝②＝③ は「ド・モルガンの法則」である。
従って、
（06）により、
（07）
① ～（Ｐ∨　Ｑ∨　Ｒ∨　Ｓ）
② 　～Ｐ＆～Ｑ＆～Ｒ＆～Ｓ
に於いて、
①＝② は「ド・モルガンの法則」である。
従って、
（08）
① ～（Ｆａ∨　Ｆｂ∨　Ｆｃ∨　Ｆｄ）
②　 ～Ｆａ＆～Ｆｂ＆～Ｆｃ＆～Ｆｄ
に於いて、
①＝② は「ド・モルガンの法則」である。
従って、
（08）により、
（09）
①（ａがＦであるか、ｂがＦであるか、ｃがＦであるか、ｄがＦである）といふことはない。
②  ａはＦではなく、ｂもＦではなく、ｃもＦではなく、ｄもＦではない。
に於いて、
①＝② は「ド・モルガンの法則」である。
然るに、
（10）
｛ｘの変域｝＝｛ａ、ｂ、ｃ、ｄ｝
であるとすると、
①（ａがＦであるか、ｂがＦであるか、ｃがＦであるか、ｄがＦである）といふことはない。
②  ａはＦではなく、ｂもＦではなく、ｃもＦではなく、ｄもＦではない。
といふことは、
①（あるｘがＦである）といふことはない。
②  すべてのｘが、Ｆではない。
といふことである。
従って、
（09）（10）により、
（11）
①（あるｘがＦである）といふことはない。
②  すべてのｘが、Ｆではない。
に於いて、
①＝② は「ド・モルガンの法則」である。
然るに、
（11）により、
（12）
①（あるｘがＦである）といふことはない。
②  すべてのｘが、Ｆではない。
といふ「日本語」は、
① ～∃ｘ（Ｆｘ）
② ∀ｘ（～Ｆｘ）
といふ「述語論理式」に「相当」する。
従って、
（11）（12）により、
（13）
① ～∃ｘ（Ｆｘ）
② ∀ｘ（～Ｆｘ）
に於いて、
①＝② は「ド・モルガンの法則」である。
然るに、
（14）
① ～∃ｘ（Ｆｘ）
② ∀ｘ（～Ｆｘ）
に於いて、
①＝② は「量化子の関係」である。
従って、
（14）により、
（15）
① ～∃ｘ（Ｆｘ）
② ∀ｘ（～Ｆｘ）
に於いて、
①＝② は「量化子の関係」であって、「ド・モルガンの法則」である。
令和０４年１１月０２日、毛利太。

「述語論理」は「命題論理」である。

（01）
（ⅰ）
１　（１）∀ｘ（Ｆｘ→～Ｇｘ）　Ａ
１　（２）　　　Ｆａ→～Ｇａ　　１ＵＥ
　３（３）　　　　　　　Ｇａ　　Ａ
　３（４）　　　　　～～Ｇａ　　３ＤＮ
１３（５）　　～Ｆａ　　　　　　２４ＭＴＴ
１　（６）　　　Ｇａ→～Ｆａ　　３５ＣＰ
１　（７）∀ｘ（Ｇｘ→～Ｆｘ）　６ＵＩ
（ⅱ）
１　（１）∀ｘ（Ｇｘ→～Ｆｘ）　Ａ
１　（２）　　　Ｇａ→～Ｆａ　　１ＵＥ
　３（３）　　　　　　　　Ｆａ　Ａ
　３（４）　　　　　　～～Ｆａ　３ＤＮ
１３（５）　　～Ｇａ　　　　　　２４ＭＴＴ
１　（６）　　　Ｆａ→～Ｇａ　　３５ＣＰ
１　（７）∀ｘ（Ｆｘ→～Ｇｘ）　６ＵＩ
従って、
（01）により、
（02）
① ∀ｘ（Ｆｘ→～Ｇｘ）
② ∀ｘ（Ｇｘ→～Ｆｘ）
に於いて、すなはち、
① すべてのｘについて、ｘがＦならば、ｘはＧではない。
② すべてのｘについて、ｘがＧならば、ｘはＦではない。
に於いて、
①＝② である。
従って、
（02）により、
（03）
① ＦはＧではない。
② ＧはＦではない。
に於いて、
①＝② である。
従って、
（03）により、
（04） 

① ＦはＧではない。
の場合、
②「逆」も必ず「真」である。
従って、 

（04）により、
（05）
例へば、
① 偶数は奇数ではない。
② 奇数は偶数ではない。
に於いて、
①＝② である。
然るに、
（06）
（ⅲ）
１　（１）～∀ｘ（Ｆｘ→～Ｇｘ）　Ａ
１　（２）∃ｘ～（Ｆｘ→～Ｇｘ）　１量化子の関係
　３（３）　　～（Ｆａ→～Ｇａ）　Ａ
　３（４）　～（～Ｆａ∨～Ｇａ）　３含意の定義
　３（５）　　　　Ｆａ＆　Ｇａ　　４ド・モルガンの法則
　３（６）　∃ｘ（Ｆｘ＆　Ｇｘ）　５ＥＩ
１　（７）　∃ｘ（Ｆｘ＆　Ｇｘ）　２３６ＥＥ
（ⅳ）
１　（１）　∃ｘ（Ｆｘ＆　Ｇｘ）　Ａ
　２（２）　　　　Ｆａ＆　Ｇａ　　Ａ
　２（３）　～（～Ｆａ∨～Ｇａ）　２ド・モルガンの法則
　２（４）　　～（Ｆａ→～Ｇａ）　３含意の定義
　２（５）∃ｘ～（Ｆｘ→～Ｇｘ）　４ＥＩ
１　（６）～∀ｘ（Ｆｘ→～Ｇｘ）　２量化子の関係
従って、
（06）により、
（07）
③（すべてのｘについて、ｘがＦならば、ｘはＧではない）といふわけではない。
④（Ｆであって、Ｇであるｘ）が存在する。
に於いて、
③＝④ である。
従って、
（07）により、
（08）
③（ＦはＧでない）といふわけではない。
④ あるＦはＧである。
に於いて、
③＝④ である。
従って、
（08）により、
（09）
例へば、
③（素数は偶数でない）といふわけではない。
④ ある素数は偶数である。
に於いて、
③＝④ である。
従って、
（05）（09）により、
（10）
① 偶数は奇数ではない。
② 奇数は偶数ではない。
③（素数は偶数でない）といふわけではない。
④ ある素数は偶数である。
に於いて、
①＝② であって、
③＝④ である。
ということに、なるものの、「だからどうした」といふ感じである。
（11）
いづれにしても、
① 偶数は奇数ではない。
② 奇数は偶数ではない。
といふことは、
①「任意の奇数」は「偶数の集合の元ではない」。
②「任意の偶数」は「奇数の集合の元ではない」。
といふことに、他ならない。

　―「量化子の関係」の「証明」―
（12）
（ⅰ）
１　　（１）　～∀ｘ（　Ｆｘ）　　Ａ
　２　（２）　～∃ｘ（～Ｆｘ）　　Ａ
　　３（３）　　　　　～Ｆａ　　　Ａ
　　３（４）　　∃ｘ（～Ｆｘ）　　３
　２３（５）　～∃ｘ（～Ｆｘ）＆
　　　　　　　　∃ｘ（～Ｆｘ）　　２４＆Ｉ
　２　（６）　　　　～～Ｆａ　　　３５ＲＡＡ
　２　（７）　　　　　　Ｆａ　　　６ＤＮ
　２　（８）　　∀ｘ（　Ｆｘ）　　７ＵＩ
１２　（９）　～∀ｘ（　Ｆｘ）＆
　　　　　　　　∀ｘ（　Ｆｘ）　　１８＆Ｉ
１　　（ア）～～∃ｘ（～Ｆｘ）　　２９ＲＡＡ
１　　（イ）　　∃ｘ（～Ｆｘ）　　アＤＮ
（ⅱ）
１　　（１）　　∃ｘ（～Ｆｘ）　　Ａ
　２　（２）　　∀ｘ（　Ｆｘ）　　Ａ
　　３（３）　　　　　～Ｆａ　　　Ａ
　２　（４）　　　　　　Ｆａ　　　２ＵＥ
　２３（５）　　～Ｆａ＆Ｆａ　　　３４＆Ｉ
　　３（６）　～∀ｘ（　Ｆｘ）　　２５ＲＡＡ
１　　（７）　～∀ｘ（　Ｆｘ）　　１３６ＥＥ
従って、
（12）により、
（13）
① ～∀ｘ（　Ｆｘ）
② 　∃ｘ（～Ｆｘ）
に於いて、すなはち、
①（全てのｘがＦである）といふわけではない。
②（Ｆでないｘ）が存在する。
に於いて、
①＝② である。

　―「量化子の関係」を「命題論理」で「証明」する。―
（14）
（ⅰ）
１　　　　（１）　～（　Ｆａ＆　Ｆｂ＆　Ｆｃ）　　Ａ
　２　　　（２）　～（～Ｆａ∨～Ｆｂ∨～Ｆｃ）　　Ａ
　　３　　（３）　　　～Ｆａ　　　　　　　　　　　Ａ
　　３　　（４）　　　～Ｆａ∨～Ｆｂ　　　　　　　３∨Ｉ
　　３　　（５）　　　～Ｆａ∨～Ｆｂ∨～Ｆｃ　　　４∨Ｉ
　２３　　（６）　～（～Ｆａ∨～Ｆｂ∨～Ｆｃ）＆
　　　　　　　　　　（～Ｆａ∨～Ｆｂ∨～Ｆｃ）　　２５＆Ｉ
　２　　　（７）　　～～Ｆａ　　　　　　　　　　　３６ＲＡＡ
　２　　　（８）　　　　Ｆａ　　　　　　　　　　　７ＤＮ
　　　９　（９）　　　　　　　～Ｆｂ　　　　　　　Ａ
　　　９　（ア）　　　～Ｆａ∨～Ｆｂ　　　　　　　９∨Ｉ
　　　９　（イ）　　　～Ｆａ∨～Ｆｂ∨～Ｆｃ　　　ア∨Ｉ
　２　９　（ウ）　～（～Ｆａ∨～Ｆｂ∨～Ｆｃ）＆
　　　　　　　　　　（～Ｆａ∨～Ｆｂ∨～Ｆｃ）　　２イ＆Ｉ
　２　　　（エ）　　　　　　～～Ｆｂ　　　　　　　９ウＲＡＡ
　２　　　（オ）　　　　　　　　Ｆｂ　　　　　　　エＤＮ
　　　　カ（カ）　　　　　　　　　　　～Ｆｃ　　　Ａ
　　　　カ（キ）　　　　　　　～Ｆｂ∨～Ｆｃ　　　カ∨Ｉ
　　　　カ（ク）　　　～Ｆａ∨～Ｆｂ∨～Ｆｃ　　　キ∨Ｉ
　２　　カ（ケ）　～（～Ｆａ∨～Ｆｂ∨～Ｆｃ）＆
　　　　　　　　　　（～Ｆａ∨～Ｆｂ∨～Ｆｃ）　　２９＆Ｉ
　２　　　（コ）　　　　　　　　　　～～Ｆｃ　　　カケＲＡＡ
　２　　　（サ）　　　　　　　　　　　　Ｆｃ　　　コＤＮ
　２　　　（シ）　　　　Ｆａ＆Ｆｂ　　　　　　　　８オ＆Ｉ
　２　　　（ス）　　　　Ｆａ＆　Ｆｂ＆　Ｆｃ　　　サシ＆Ｉ
１２　　　（セ）　　～（Ｆａ＆　Ｆｂ＆　Ｆｃ）＆
　　　　　　　　　　　（Ｆａ＆　Ｆｂ＆　Ｆｃ）　　２ス＆Ｉ
１　　　　（ソ）～～（～Ｆａ∨～Ｆｂ∨～Ｆｃ）　　２セＲＡＡ
１　　　　（タ）　　　～Ｆａ∨～Ｆｂ∨～Ｆｃ　　　ソＤＮ
（ⅱ）
１　　　　　（１）　　～Ｆａ∨～Ｆｂ∨～Ｆｃ　　　Ａ
　２　　　　（２）　　　Ｆａ＆　Ｆｂ＆　Ｆｃ　　　Ａ
１　　　　　（３）　（～Ｆａ∨～Ｆｂ）∨～Ｆｃ　　２結合法則
　　４　　　（４）　（～Ｆａ∨～Ｆｂ）　　　　　　Ａ
　　　５　　（５）　　～Ｆａ　　　　　　　　　　　Ａ
　２　　　　（６）　　　　Ｆａ　　　　　　　　　　２＆Ｅ
　２　５　　（７）　　～Ｆａ＆Ｆａ　　　　　　　　５６＆Ｉ
　　　５　　（８）　　～（Ｆａ＆　Ｆｂ＆　Ｆｃ）　２７ＲＡＡ
　　　　９　（９）　　　　　　～Ｆｂ　　　　　　　Ａ
　２　　　　（ア）　　　　　　　Ｆｂ　　　　　　　２＆Ｅ
　２　　９　（イ）　　　～Ｆｂ＆Ｆｂ　　　　　　　９ア＆Ｉ
　　　　９　（ウ）　　～（Ｆａ＆　Ｆｂ＆　Ｆｃ）　２イＲＡＡ
　　４　　　（エ）　　～（Ｆａ＆　Ｆｂ＆　Ｆｃ）　４５８９ウ∨Ｅ
　　　　　オ（オ）　　　　　　　　　　　～Ｆｃ　　Ａ
　２　　　　（カ）　　　　　　　　　　　Ｆｃ　　　２＆Ｅ
　２　　　オ（キ）　　　　　　　～Ｆｃ＆Ｆｃ　　　オカ＆Ｉ
　　　　　オ（ク）　　～（Ｆａ＆　Ｆｂ＆　Ｆｃ）　２キＲＡＡ
１　　　　　（コ）　　～（Ｆａ＆　Ｆｂ＆　Ｆｃ）　１４エオク∨Ｅ
従って、
（14）により、
（15）
① ～（　Ｆａ＆　Ｆｂ＆　Ｆｃ）
② 　　～Ｆａ∨～Ｆｂ∨～Ｆｃ
に於いて、すなはち、
①（ａがＦであって、ｂもＦであって、ｃもＦである）といふことはない。
②（ａがＦでないか、ｂがＦでないか、ｃがＦでないか）の何れかである。
に於いて、
①＝② である。
然るに、
（16）
｛ｘの変域｝＝｛ａ、ｂ、ｃ｝
であるならば、
①（ａがＦであって、ｂもＦであって、ｃもＦである）といふことはない。
②（ａがＦでないか、ｂがＦでないか、ｃがＦでないか）の何れかである。
に於いて、
①＝② であるといふことは、
①（全てのｘがＦである）といふわけではない。
②（Ｆでないｘ）が存在する。
に於いて、
①＝② である。
といふことに、他ならない。
然るに、
（17）
①（全てのｘがＦである）といふわけではない。
②（Ｆでないｘ）が存在する。
に於いて、
①＝② である。
といふことは、
① ～∀ｘ（　Ｆｘ）
② 　∃ｘ（～Ｆｘ）
に於いて、
①＝② である。
といふことに、他ならない。
従って、
（15）（16）（17）により、
（18）
｛ｘの変域｝＝｛ａ、ｂ、ｃ｝
であるならば、
① ～∀ｘ（　Ｆｘ）
② 　∃ｘ（～Ｆｘ）
③ （すべてのｘがＦである）といふわけではない。
④ （Ｆでないｘ）が存在する。
⑤ ～（　Ｆａ＆　Ｆｂ＆　Ｆｃ）
⑥   （～Ｆａ∨～Ｆｂ∨～Ｆｃ）
⑦ （ａがＦであって、ｂもＦであって、ｃもＦである）といふことはない。
⑧ （ａがＦでないか、ｂがＦでないか、ｃがＦでないか）の何れかである。
に於いて、
①＝②＝③＝④＝⑤＝⑥＝⑦＝⑧ である。
従って、
（18）により、
（19）
「述語論理」は、「命題論理」に他ならない。
令和０４年１１月０１日、毛利太。

「法律家」にも「論理学」は「必要」である。

（01）
１　　（１）Ｐ＆Ｑ⇔Ｒ　　　　　Ａ
１　　（２）Ｐ＆Ｑ→Ｒ　　　　　１Ｄｆ．⇔
　２　（３）　　　～Ｒ　　　　　Ａ
１２　（４）～Ｐ∨～Ｑ　　　　　２３ＭＴＴ
１２　（５）～Ｑ∨～Ｐ　　　　　４交換法則
１２　（６）　Ｑ→～Ｐ　　　　　５含意の定義
１　　（７）～Ｒ→（Ｑ→～Ｐ）　２６ＣＰ
　　８（８）Ｑ＆～Ｒ　　　　　　Ａ
　　８（９）　　～Ｒ　　　　　　８＆Ｅ
１　８（ア）　　　　Ｑ→～Ｐ　　７９ＭＰＰ
　　８（イ）Ｑ　　　　　　　　　８＆Ｅ
１　８（ウ）　　　　　　～Ｐ　　アイＭＰＰ
１　　（エ）Ｑ＆～Ｒ→　～Ｐ　　８ウＣＰ
従って、
（02）
① Ｐ＆Ｑ⇔Ｒ├ Ｑ＆～Ｒ→～Ｐ
という「連式」は、「妥当」である。
従って、
（02）により、
（03）
Ｐ＝不注意である。
Ｑ＝誤診である。
Ｒ＝有罪である。
とする。
従って、
（02）（03）により、
（04）
（ⅰ）「不注意による誤診であるならば、そのときに限って、有罪である。」従って、
（ⅱ）「誤診であっても、無罪ならば、不注意ではない。」
という「推論」は「妥当」である。
然るに、
（05）
１　　（１）　　Ｑ＆～Ｒ→～Ｐ　Ａ
　２　（２）　　　　　　　　Ｐ　Ａ
　２　（３）　　　　　　～～Ｐ　２ＤＮ
１２　（４）～（Ｑ＆～Ｒ）　　　１３ＭＴＴ
１２　（５）～Ｑ∨～～Ｒ　　　　４ド・モルガンの法則
１２　（６）～～Ｒ∨～Ｑ　　　　５交換法則
１２　（７）　～Ｒ→～Ｑ　　　　６含意の定義
１　　（８）Ｐ→（～Ｒ→～Ｑ）　２７ＣＰ
　　９（９）Ｐ＆～Ｒ　　　　　　Ａ
　　９（ア）Ｐ　　　　　　　　　９＆Ｅ
１　９（イ）　　　～Ｒ→～Ｑ　　８アＭＰＰ
　　９（ウ）　　　～Ｒ　　　　　９＆Ｅ
１　９（エ）　　　　　　～Ｑ　　イウＭＰＰ
１　　（オ）Ｐ＆～Ｒ→　～Ｑ　　９エＣＰ
従って、
（05）により、
（06）
② Ｑ＆～Ｒ→～Ｐ├ Ｐ＆～Ｒ→～Ｑ
という「連式」は、「妥当」である。
従って、
（03）（06）により、
（07）
（ⅱ）「誤診　であっても、無罪ならば、不注意ではない。」従って、
（ⅲ）「不注意であっても、無罪ならば、　誤診ではない。」
という「推論」は「妥当」である。
従って、
（04）（07）により、
（08）
（ⅰ）「不注意による誤診であるならば、そのときに限って、有罪である。」従って、
（ⅲ）「不注意であっても、無罪ならば、誤診ではない。」
という「推論」は「妥当」である。
従って、
（08）により、
（09）
弁護士：不注意による誤診であるならば、そのときに限って、有罪である。
依頼人：分かりました。ということは、不注意であっても、無罪ならば、誤診ではないのですね？
という「会話」がなされるなら、「論理学が得意な弁護士」であれば、直ちに、
弁護士：そうです。不注意であっても、無罪ならば、誤診ではありません。
という風に、「即答」することになる。
従って、
（09）により、
（10）
依頼人：分かりました。ということは、不注意であっても、無罪ならば、誤診ではないのですね？
という「質問」に対して、
弁護士：そうです。不注意であっても、無罪ならば、誤診ではありません。
という風に、　「即答」出来ないとすれば、
その弁護士は、「論理」というものが、分かっていないので、
その弁護士は、「論理的な思考」ということが、苦手な弁護士である。
という、ことになる。
（11）
思うに、「人の運命を左右」するのだから、「法学部」こそ、「論理学」を「必修」にすべきである。
令和０４年１０月２７日、毛利太。

「医療過誤に於ける医師の責任」と「ド・モルガンの法則」。

（01）
このところ、『告訴状』を書くのに忙しくて、「ブログ」を書けていなかったのですが、
（02）
（ⅰ）
１　　（１）～（Ｐ∨Ｑ）　　　　　　　Ａ
　２　（２）　　Ｐ　　　　　　　　　　Ａ
　２　（３）　　Ｐ∨Ｑ　　　　　　　　２∨Ｉ
１２　（４）～（Ｐ∨Ｑ）＆（Ｐ∨Ｑ）　１４＆Ｉ
１　　（５）　～Ｐ　　　　　　　　　　２ＲＡＡ
　　６（６）　　　　Ｑ　　　　　　　　Ａ
　　６（７）　　Ｐ∨Ｑ　　　　　　　　６∨Ｉ
１　６（８）～（Ｐ∨Ｑ）＆（Ｐ∨Ｑ）　１７＆Ｉ
１　　（９）　　　～Ｑ　　　　　　　　６ＲＡＡ
１　　（ア）～Ｐ＆～Ｑ　　　　　　　　５９＆Ｉ
（ⅱ）
１　　　（１）　　～Ｐ＆～Ｑ　　　　　　　　Ａ
　２　　（２）　　　Ｐ∨　Ｑ　　　　　　　　Ａ
１　　　（３）　　～Ｐ　　　　　　　　　　　１＆Ｅ
　　４　（４）　　　Ｐ　　　　　　　　　　　Ａ
１　４　（５）　　～Ｐ＆～Ｐ　　　　　　　　３４＆Ｉ
　　４　（６）～（～Ｐ＆～Ｑ）　　　　　　　１５ＲＡＡ
　　　７（７）　　　　　　Ｑ　　　　　　　　Ａ
１　　　（８）　　　　　～Ｑ　　　　　　　　１＆Ｅ
１　　７（９）　　　Ｑ＆～Ｑ　　　　　　　　７８＆Ｉ
　　　７（ア）～（～Ｐ＆～Ｑ）　　　　　　　１９ＲＡＡ
　２　　（イ）～（～Ｐ＆～Ｑ）　　　　　　　２４６７ア
１２　　（ウ）（～Ｐ＆～Ｑ）＆～Ｐ＆～Ｑ）　１イ＆Ｉ
１　　　（エ）　～（Ｐ∨　Ｑ）　　　　　　　２ウＲＡＡ
従って、
（02）により、
（03）
① ～（Ｐ∨　Ｑ）
② 　～Ｐ＆～Ｑ
に於いて、
①＝② は、「ド・モルガンの法則」である。
従って、
（03）により、
（04）
③ ～～（Ｐ∨　Ｑ）
④ ～（～Ｐ＆～Ｑ）
に於いて、
③＝④ は、「ド・モルガンの法則」である。
従って、
（04）により、
（05）
「二重否定律（ＤＮ）」により、
③ 　　（Ｐ∨　Ｑ）
④ ～（～Ｐ＆～Ｑ）
に於いて、
③＝④ は、「ド・モルガンの法則」である。
従って、
（03）（05）により、
（06）
① 　～（Ｐ∨　Ｑ）
② 　　～Ｐ＆～Ｑ
③ 　　（Ｐ∨　Ｑ）
④ ～（～Ｐ＆～Ｑ）
に於いて、すなわち、
①（Ｐか、または、Ｑである）ということはない。
②　Ｐではないし、Ｑでもない。
③（Ｐか、または、Ｑである）。
④（Ｐではないし、Ｑでもない）ということはない。
に於いて、
①＝② は、「ド・モルガンの法則」であって、
③＝④ は、「ド・モルガンの法則」である。
然るに、
（07）
（ⅰ）
１　　（１）　　Ｐ∨Ｑ　⇔Ｒ　　　　　　　　　　　　　　Ａ
１　　（２）｛（Ｐ∨Ｑ）→Ｒ｝＆（Ｒ→（Ｐ∨Ｑ）｝　　　１Ｄｆ.⇔
１　　（３）　　Ｐ∨Ｑ　→Ｒ　　　　　　　　　　　　　　２＆Ｅ
　４　（４）　　　　　　～Ｒ　　　　　　　　　　　　　　Ａ
１４　（５）～（Ｐ∨Ｑ）　　　　　　　　　　　　　　　　３４ＭＴＴ
１４　（６）～Ｐ＆～Ｑ　　　　　　　　　　　　　　　　　５ド・モルガンの法則
１　　（７）～Ｒ→（～Ｐ＆～Ｑ）　　　　　　　　　　　　４６ＣＰ
１　　（８）　　　　　　　　　　　Ｒ→（Ｐ∨Ｑ）　　　　２＆Ｅ
　　９（９）　　　　　　　　　　　（～Ｐ＆～Ｑ）　　　　Ａ
　　９（ア）　　　　　　　　　　　　～（Ｐ∨Ｑ）　　　　９ド・モルガンの法則
１　９（イ）　　　　　　　　　　～Ｒ　　　　　　　　　　８アＭＴＴ
１　　（ウ）　　　　　　　　　　　（～Ｐ＆～Ｑ）→～Ｒ　９イＣＰ
１　　（エ）～Ｒ→（～Ｐ＆～Ｑ）＆（～Ｐ＆～Ｑ）→～Ｒ　７ウ＆Ｉ
１　　（オ）～Ｒ⇔（～Ｐ＆～Ｑ）　　　　　　　　　　　　エＤｆ.⇔
（ⅱ）
１　　（１）　～Ｒ⇔（～Ｐ＆～Ｑ）　　　　　　　　　　　　Ａ
１　　（２）　～Ｒ→（～Ｐ＆～Ｑ）＆（～Ｐ＆～Ｑ）→～Ｒ　１Ｄｆ.⇔
１　　（３）　～Ｒ→（～Ｐ＆～Ｑ）　　　　　　　　　　　　２＆Ｅ
　４　（４）　　　　　Ｐ∨　Ｑ　　　　　　　　　　　　　　Ａ
１　　（５）　　～（～Ｐ＆～Ｑ）　　　　　　　　　　　　　４ド・モルガンの法則
１４　（６）～～Ｒ　　　　　　　　　　　　　　　　　　　　３５ＭＴＴ
１４　（７）　　Ｒ　　　　　　　　　　　　　　　　　　　　６ＤＮ
１　　（８）（Ｐ∨Ｑ）→Ｒ　　　　　　　　　　　　　　　　４７ＣＰ
１　　（９）　　　　　　　　　　　　（～Ｐ＆～Ｑ）→～Ｒ　２＆Ｅ
　　９（ア）　　　　　　　　　　　　　　　　　　　　　Ｒ　Ａ
　　９（イ）　　　　　　　　　　　　　　　　　　　～～Ｒ　アＤＮ
１　９（ウ）　　　　　　　　　　　～（～Ｐ＆～Ｑ）　　　　９イＭＴＴ
１　９（エ）　　　　　　　　　　　　　　Ｐ∨　Ｑ　　　　　ウ、ド・モルガンの法則
１　　（オ）　　　　　　　　　　　Ｒ→（Ｐ∨　Ｑ）　　　　９エＣＰ
１　　（カ）（Ｐ∨Ｑ）→Ｒ＆　　　Ｒ→（Ｐ∨　Ｑ）　　　　８オ＆Ｉ
１　　（キ）　Ｐ∨Ｑ　⇔Ｒ　　　　　　　　　　　　　　　　カＤｆ.⇔
従って、
（07）により、
（08）
① （Ｐ∨Ｑ）⇔Ｒ
② ～Ｒ⇔（～Ｐ＆～Ｑ）
に於いて、
①＝② である。
従って、
（08）により、
（09）
① （Ｐ∨ Ｑ）⇔ Ｒ
②（～Ｐ＆～Ｑ）⇔～Ｒ
に於いて、
①＝② である。
従って、
（09）により、
（10）
Ｐ＝予見は不可能。
Ｑ＝回避も不可能。 Ｒ＝患者の死に対して、医師には責任が無い。
であるとして、
①（予見が不可能であるか、または、回避が不可能である）　　　ならば、そのときに限って、患者の死に対して、医師には責任が無い。
②（予見は不可能ではなかったし　、回避も不可能ではなかった）ならば、そのときに限って、患者の死に対して、医師には責任が有る。
に於いて、
①＝② である。
然るに、
（11）
「白い巨塔（2003年、フジＴＶ）」を見るか限り、
①（予見が不可能であるか、または、回避が不可能である）　　　ならば、そのときに限って、患者の死に対して、医師には責任が無い。
②（予見は不可能ではなかったし　、回避も不可能ではなかった）ならば、そのときに限って、患者の死に対して、医師には責任が有る。
に於いて、
①＝② であって、尚且つ、
① は「真」であり、
② も「真」である。
従って、
（11）により、
（12）
① 患者の死に対して、医師には責任が無い。
② 患者の死に対して、医師には責任が有る。
に於いて、
国平弁護士が、① を「主張」する以上、
関口弁護士が、② を「主張」する以上、
両者はともに、
①   （Ｐ∨ Ｑ）⇔  Ｒ
②（～Ｐ＆～Ｑ）⇔～Ｒ
に於いて、
①＝② である。
という「等式」を「真」であると、「信じている」。
ということになる。
然るに、
（13）
私自身は、「医療訴訟」に於いて、

という「証拠（禁忌薬剤による急性腎不全を契機とした非閉塞性腸管虚血）」に基づき、
②（予見は不可能ではなかったし、回避も不可能ではなかった）が故に、患者の死に対して、医師には責任が有る。
という風に、「主張」するつもりでいます。
然るに、
（14）

従って、
（11）（14）により、
（15）
「東大法卒のおっさん」のような方は、
①（予見が不可能であるか、または、回避が不可能である）　　　ならば、そのときに限って、患者の死に対して、医師には責任が無い。
②（予見は不可能ではなかったし　、回避も不可能ではなかった）ならば、そのときに限って、患者の死に対して、医師には責任が有る。
に於いて、
①＝② である。
ということを、「計算（Proposional calculus）」によって、示すことが、出来ないものと思われるが、
このことは、「法律家にとって、決して、好ましいことではない」ものと思われる。
令和０４年１０月１４日、毛利太。

「論理学」は「診断」にも「役に立つ」。

（01）
脱水によって体内の水分が減少し血液の濃縮が起こり、腎機能が低下します。
そのことによって、次のような数値が上昇することがわかっています。
・赤血球数（RBC）・ヘモグロビン値（Hb）・ヘマトクリット（Ht）
・総たんぱく（TP）・アルブミン（Alb）
・尿素窒素（UN）・クレアチニン（Cr）
・尿酸（UA）
従って、
（01）により、
（02）
（ⅰ）脱水によって腎機能が悪化しているのであれば、赤血球とクレアチニンは並行して増大しなければならない。
然るに、
（03）

然るに、
（04）
「赤血球」の「小さい順」に、「日付」を「並び替え」ると、

然るに、
（05）
「赤血球」だけであれば、

然るに、
（06）
「クレアチニン」だけであれば、

従って、
（05）（06）により、
（07）
①「赤血球の値」が「大きく」なれば、「クレアチニンの値」も「大きく」なる。
②「赤血球の値」が「小さく」なれば、「クレアチニンの値」は「大きく」なる。
に於いて、
① は「ウソ」であって、
② も「ウソ」である。
従って、
（07）により、
（08）
①「赤血球の値」と「クレアチニンの値」には、「正の相関は、無い」し、
②「赤血球の値」と「クレアチニンの値」には、「負の相関も、無い」。
従って、
（08）により、
（09）
（ⅱ）赤血球とクレアチニンは並行して増大していない。
然るに、
（10）

然るに、
（11）
（ⅲ）腎機能が悪化している。
従って、
（02）（09）（11）により、
（12）
（ⅰ）脱水によって腎機能が悪化しているのであれば、赤血球とクレアチニンは並行して増大しなければならない。
（ⅱ）赤血球とクレアチニンは並行して増大していない。
（ⅲ）腎機能が悪化している。
という「命題」は、「３つとも真である」。
然るに、
（13）
１　　（１）Ｐ＆Ｑ→Ｒ　　仮定
　２　（２）　　　～Ｒ　　仮定
１２　（３）～（Ｐ＆Ｑ）　１２ＭＴＴ
１２　（４）～Ｐ∨～Ｑ　　３ド・モルガンの法則
１２　（５）～Ｑ∨～Ｐ　　４交換法則
１２　（６）　Ｑ→～Ｐ　　５含意の定義
　　７（７）　Ｑ　　　　　仮定
１２７（８）　　　～Ｐ　　６７ＭＰＰ
という「推論」は「妥当」である。
然るに、
（14）
Ｐ＝脱水である。
Ｑ＝腎機能が悪化する。
Ｒ＝赤血球・クレアチニンは並行して変化する。
であるとする。
従って、
（13）（14）により、
（15）
（１）脱水によって腎機能が悪化しているのであれば、
　　　赤血球とクレアチニンは並行して増大しなければならない。
（２）然るに、「検査結果」を見る限り、当該の患者の、
　　　赤血球とクレアチニンは並行して変化しない。従って、
（３）脱水によって、　腎機能が悪化している。というわけではない。従って、
（４）脱水でないか、　腎機能が悪化していないか、どちらかである。従って、
（５）腎機能が悪化していないか、　脱水でないか、どちらかである。従って、
（６）腎機能が悪化しているならば、脱水ではない。然るに、
（７）腎機能が悪化している。従って、
（８）脱水ではない（選言三段論法）。
という「推論」は、「妥当」である。
従って、
（12）～（15）により、
（16）
（ⅰ）脱水によって腎機能が悪化しているのであれば、赤血球とクレアチニンは並行して増大しなければならない。然るに、
（ⅱ）赤血球とクレアチニンは並行して増大していない。然るに、
（ⅲ）腎機能が悪化している。従って、
（ⅳ）脱水ではない。
といふ「推論」は「妥当」であって、尚且つ、
（ⅳ）脱水ではない。
という「結論（命題）」は、「真」である。
然るに、
（17）
１　　（１）Ｐ＆Ｑ→Ｒ　　仮定
　２　（２）　　　～Ｒ　　仮定
１２　（３）～（Ｐ＆Ｑ）　１２ＭＴＴ
１２　（４）～Ｐ∨～Ｑ　　３ド・モルガンの法則
１２　（５）～Ｑ∨～Ｐ　　４交換法則
１２　（６）　Ｑ→～Ｐ　　５含意の定義
　　７（７）　Ｑ　　　　　仮定
１２７（８）　　　～Ｐ　　６７ＭＰＰ
という「推論」に加えて、
１　　　（１）Ｐ＆Ｑ→Ｒ　　仮定
　２　　（２）　　　～Ｒ　　仮定
　　３　（３）　　Ｑ　　　　仮定
　　　４（４）Ｐ　　　　　　仮定
　　３４（５）Ｐ＆Ｑ　　　　３４＆Ｉ
１２３４（６）　　　　Ｒ　　１５ＭＰＰ
１２３４（７）　～Ｒ＆Ｒ　　２６＆Ｉ
１２３　（８）～Ｐ　　　　　４７ＲＡＡ
という「推論」も「妥当」である。
従って、
（14）（17）により、
（18）
（１）脱水によって腎機能が悪化しているのであれば、
　　　赤血球とクレアチニンは並行して増大しなければならない。然るに、
（２）「検査結果」を見る限り、当該の患者の、
　　　赤血球とクレアチニンは並行して変化していない。然るに、
（３）腎機能は悪化している。従って、その上、仮に、
（４）脱水であるとするならば、
（５）脱水であって、尚且つ、腎機能が悪化していることになり、そのため、
（６）赤血球とクレアチニンは並行して増大しなければならないが、実際には、
（７）赤血球とクレアチニンは並行して増大していないので、矛盾する。従って、
（８）脱水ではない。
従って、
（10）（15）（18）により、
（19）

とは言うものの、実際には、
（８）脱水ではない。
従って、
（19）により、
（20）
12. 2019/1/19から輸液を中止しましたが、翌1/20から食事摂取量が不安定～低下しております（電子カルテ温度板参照）。高齢の患者様はもともとの生理的予備能が低下していることもあり、嘔吐や下痢などの症状がなくとも食事摂取量が低下すれば脱水状態を発症・継続することは容易に起こりうることです（2019/1/25の血液検査結果（ヘマトクリット上昇、食事摂取量低下にもかかわらずアルブミン上昇、ナトリウム上昇）から脱水状態であると確認したため同日より輸液再開しております）。
という『診断』は、『誤診』である。
然るに、
（21）
「説明」は「省略」するものの、「右の診断」が『誤診』であることは、

という「グラフ」からも、「明白」である。

令和４年９月１９日、毛利太。

「脱水」ではない「理由」。

 （01）

郵便番号 住所　氏名　電話番号

と、申します。

（02）

令和４年９月１３日に、「申立書」に対する「追加の資料」を送付させてもらい、早速、

令和４年９月１４日に、Ｋ様より、電話にて、「この他に、追加の資料は有りますか」

という「質問」を受けています。

（03）

そして、その際には、「追加の資料は無い」と答えさせてもらったのですが、その後、

として、病院より、（04）で示す「回答」を受け取ることになったので、「１度は無い」と言っていることから、ずいぶんと迷ってはみたのですが、敢えて、「追加の資料」を郵送させてもらうことにしました。

（04）

従って、

（04）により、

（05）

①「通常の身長体重計を用いた実測値」

②「体重を計測できるストレッチャー又はベッドでの実測値」

③「計算アプリによる実測値」

という「計測」により、いずれにしても、「ＡＢＣＤ（受理番号＃＃＃＃＃）の体重」は、

４８.９ｋｇ（２０１７年０２月２８日） ４８.９ｋｇ（２０１８年１２月２１日） ４９.０ｋｇ（２０１９年０１月１０日）

であったということが、「確認」出来ました。

従って、

（05）により、

（06）

２０１７年０２月２８日（４８.９ｋｇ） ２０１８年１２月２１日（４８.９ｋｇ）

であったため、「１年と１０カ月」に渡って、

「ＡＢＣＤ（受理番号12345）の体重に、増減は、全く有りません。」

然るに、

（07）

２２カ月間に渡って、ＡＢＣＤ（受理番号12345）の体重に、増減は無い。

ということは、

入院当日（１２月２１日）の８日前の、ＡＢＣＤの食事の量も、十分であった。

ということに対する、「傍証」となっています。

従って、

（07）により、

（08）

「追加の資料（令和０４年０９月１３日）」の中で示した、

「普段の食欲」は「普通」。 「体温３７.２度（微熱）」。 「軽度発赤」、腫脹、疼痛あり。

という「記録（問診票・カルテ）」と、今示した、

２２カ月間に渡って、ＡＢＣＤ（受理番号12345）の体重に、増減は無い。

という「傍証」とによって、

「１２月１３日（入院の８日前）」の時点では、

（ａ）「歩行による通院、買い物」等も「可能」であり、 （ｂ）「普段通リに食事（３食）」が摂れ、「お茶」をよく飲み、 （ｃ）「排便・排尿・睡眠」も「問題なし」です。

ということが、「事実」であった。

ということは、「納得してもらえる」ものと、考えます

然るに、

（09）

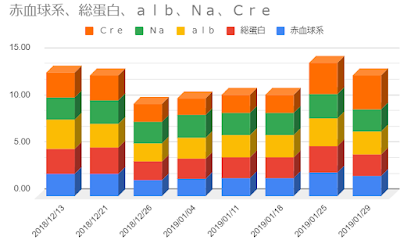
検査日	赤血球系	総蛋白	アルブミン	ナトリウム	点滴	服用中の薬
2018/12/13	2.34	2.69	3.04	2.37	無し	無し
2018/12/21	2.36	2.81	2.48	2.54	無し	無し
2018/12/26	1.93	2.29	1.92	2.34	有り	無し
2019/01/04	1.70	1.98	1.92	2.30	有り	無し
2019/01/11	1.79	2.17	2.24	2.39	有り	フェブリク
2019/01/18	1.93	2.21	2.32	2.34	有り	フェブリク
2019/01/25	2.47	2.81	2.96	2.59	無し	フェブリク
2019/01/29	2.10	2.33	2.4	2.39	有り	フェブリク

従って、

（08）（09）により、

（10）

検査日	赤血球系	総蛋白	アルブミン	ナトリウム	点滴	服用中の薬
2018/12/13	2.34	2.69	3.04	2.37	無し	無し
2019/01/18	1.93	2.21	2.32	2.34	有り	フェブリク
2019/01/25	2.47	2.81	2.96	2.59	無し	フェブリク

という「表とグラフ」から「言える」こととしては、

（ⅰ）２０１８年０１月１８日、点滴を中止したところ、 （ⅱ）２０１９年０１月２５日の「血液検査の結果」は、 （ⅲ）２０１８年１２月１３日と「同じような数値」となって、尚且つ、 （ⅳ）２０１８年１２月１３日に於いて、森田米生は「脱水」ではない。

ということになります。

然るに、

（11）

『然るべき計算』により、

検査日	赤血球系	総蛋白	ａｌｂ	Ｎａ	Ｃｒｅ	ＢＵＮ	点滴	服用中の薬
12/13	2.34	2.69	3.04	2.37	2.63	1.83	無し	無し
01/18	1.93	2.21	2.32	2.34	1.91	1.39	有り	フェブリク
01/25	2.47	2.81	2.96	2.59	3.31	4.23	無し	フェブリク

という「表とグラフ」から「言える」こととしては、

（ⅰ）２０１８年０１月１８日、点滴を中止したところ、 （ⅱ）２０１９年０１月２５日の「（CreとBUN以外の）検査の結果」は、 （ⅲ）２０１８年１２月１３日と「同じような数値」となって、尚且つ、 （ⅳ）２０１８年１２月１３日に於いて、森田米生は「脱水」ではない。

ということになります。

従って、

（11）により、

（12）

という「診療」は、

（ⅰ）「０１月１８日」と「０１月２５日」は「比較」していても、 （ⅱ）「１２月１３日」と「０１月２５日」は「比較」していない。 （ⅲ）「クレアチニンと尿素窒素の検査結果」を「無視」している。

という「理由」により、「正しい診療」ではない。

と、すべきです。

令和０４年０９月１８日

ＥＦＧＨ