「返り点・括弧」の条件。

―「１０月２９日の記事」を書き換へます。―
（01）
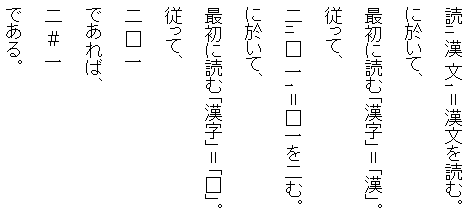
① 訓‐読（漢文）＝
① ３‐４（１２）⇒
①（１２）３‐４＝
①（漢文）訓‐読＝
①（漢文を）訓‐読す。
然るに、
（02）
囗＝訓読
といふ「漢字」が、有るものとする。
従って、
（01）（02）により、
（03）
② 囗（漢文）＝
② ３（１２）⇒
② （１２）３＝
② （漢文）囗＝
② （漢文を）囗す＝
② （漢文を）訓読す。
従って、
（01）（03）により、
（04）
② ３　１　２
① ３‐４　１　２
といふ「順番」の「返り点・括弧」を考へることは、
② ３　１　２
といふ「順番」の「返り点・括弧」を考へることに、等しい。
ｃｆ.

（05）

従って、
（05）により、
（06）
③ ５  ２　１　４　３
② ７　３　１‐２　６　４‐５
① ９　４　１‐２‐３　８　５‐６‐７
といふ「順番」の「返り点・括弧」を考へることは、
③ ５  ２　１　４　３
といふ「順番」の「返り点・括弧」を考へることに、等しい。
（07）
「未」「將」「當」「應」「宜」「須」「猶」「盍」などの諸字は、一字でありながら、最初副詞によみ、次に動詞あるいは助動詞と読むのが慣例となっている。― 中略 ―「未」は「いまダ～ず」とよみ、「まだ～しない」の意で、「尚不」と同じである（中沢希男・澁谷玲子、漢文訓読の基礎、1985年、９０頁）。
従って、
（07）により、
（08）
未＿〔嘗読（漢文）〕＝
尚不〔嘗読（漢文）〕⇒
１６〔２５（３４）〕＝
１〔２（３４）５〕６＝
未〔嘗（漢文）読〕不＝
未だ〔嘗て（漢文を）読ま〕不。
然るに
（09）
ＱＵＥＭ　ＬＩＢＲＵＭ　ＬＥＧＩＳ＝
あなたは　何の　本を　読んでいるの？
（ｃｆ.白水社、ＣＤエクスプレス　ラテン語、2004年、７１頁）
従って、
（08）（09）により、
（10）
ＱＵＥＭ　ＬＩＢＲＵＭ　ＬＥＧＩＳ？
に於いて、
ＬＥＧＩＳ
といふ「再読文字」は、「一語」であるが、最初に「主語（ＩＳ）」に読み、最後に「動詞（ＬＥＧ）」として読むことになる。
従って、
（11）
２ｎｄ＝ＱＵＥＭ
３ｒｄ＝ＬＩＢＲＵＭ
４ｔｈ＝ＬＥＧ
１ｓｔ＝ＩＳ
の「順」である。
従って、
（12）
二＝ＱＵＥＭ
三＝ＬＩＢＲＵＭ
四＝ＬＥＧ
一＝ＩＳ
である。
ｃｆ.

然るに、
（13）
二＝ＱＵＥＭ
二＝ＬＩＢＲＵＭ
二＝ＬＥＧ
一＝ＩＳ
といふ「それ」が、「返り点」であるならば、
１ｓｔ ＝本を
２ｎｄ＝読んでゐる
３ｒｄ ＝あなたは
４ｔｈ ＝何の。
といふ「順番」となるため、
あなたは　何の　本を　読んでゐる。
といふ「訓読」には、ならない。
（14）
二＝ＱＵＥＭ
二＝ＬＩＢＲＵＭ
三＝ＬＥＧ
一＝ＩＳ
といふ「それ」が、「返り点」であるならば、
１ｓｔ ＝本を
２ｎｄ＝あなたは
３ｒｄ ＝何の
４ｔｈ ＝読んでゐる。
といふ「順番」となるため、
あなたは　何の　本を　読んでゐる。
といふ「訓読」には、ならない。
（15）
二＝ＱＵＥＭ
三＝ＬＩＢＲＵＭ
二＝ＬＥＧ
一＝ＩＳ
といふ「それ」が、「返り点」であるならば、
１ｓｔ ＝読んでゐる
２ｎｄ＝あなたは
３ｒｄ ＝何の
４ｔｈ ＝本を。
といふ「順番」となるため、
あなたは　何の　本を　読んでゐる。
といふ「訓読」には、ならない。
従って、
（12）～（15）により、
（16）
ＱＵＥＭ　ＬＩＢＲＵＭ　ＬＥＧＩＳ＝
あなたは　何の　本を　読んでゐる。
に対する「返り点」は、
二＝ＱＵＥＭ
三＝ＬＩＢＲＵＭ
四＝ＬＥＧ
一＝ＩＳ
以外には、有り得ない。
然るに、
（17）
「返り点」は、「縦書き」であれば、「下から、上へ返る、返り点」であって、それ故、
「返り点」は、「横書き」であれば、「右から、左へ返る、返り点」であって、それ故、
「横書き」であれば、「左から、右へ返る」場合の「それ」は、「返り点」ではない。
然るに、
（18）
二　三　四　一　
であれば、
二→三　は、「左から右へ」返ってゐて、
三→四　も、 「左から右へ」返ってゐる。
従って、
（16）（17）（18）により、
（19）
① ＱＵＥＭ　ＬＩＢＲＵＭ　ＬＥＧＩＳ＝
① あなたは　何の　本を　読んでゐる。
といふ「ラテン語訓読」に対しては、「返り点」を加へることが、出来ない。
（20）
① 二　三　四　一
② 二　四　三　一
が「算用数字」であれば、
① ２　３　４　１
② ２　４　３　１
であって、
① ２＜３＜４＞１　＆　２＝１＋１
② ２＜４＞３＞１　＆　２＝１＋１
である。
然るに、
（21）
① ２（３〔４［１）〕］
② ２（４［３〔１）〕］
③ ４［３〔２（１）〕］
に於いて、
① ２（　）⇒（　）２
② ２（　）⇒（　）２
③ ２（　）⇒（　）２
① ３〔　〕⇒〔　〕３
② ３〔　〕⇒〔　〕３
③ ３〔　〕⇒〔　〕３
① ４［　］⇒［　］４
② ４［　］⇒［　］４
③ ４［　］⇒〔　〕４
とするならば、
① （〔［１）２〕３］４
② （［〔１）２〕３］４
③ ［〔（１）２〕３］４
である。
然るに、
（22）
③ ［ 〔 （　） 〕 ］
は「括弧」であるが、
① （ 〔 ［　） 〕 ］
② （ ［ 〔　） 〕 ］
は「括弧」ではない。
従って、
（19）、（20）～（22）により、
（23）
① ＱＵＥＭ　ＬＩＢＲＵＭ　ＬＥＧＩＳ＝
① あなたは　何の　本を　読んでゐる。
といふ「ラテン語訓読」に対しては、「返り点」と「括弧」を加へることが、出来ない。
（24）
④ １２（１３〔１１）〕
⑤ １３〔１２（１１）〕
に於いて、
④ １２（　）⇒（　）１２
④ １２（　）⇒（　）１２
⑤ １３〔　〕⇒〔　〕１３
⑤ １３〔　〕⇒〔　〕１３
とするならば、
④ （〔１１）１２〕１３
⑤ 〔（１１）１２〕１３
である。
然るに、
（25）
⑤ 〔 （　） 〕
は「括弧」であるが、
④ （ 〔　） 〕
は「括弧」ではない。
従って、
（21）（22）、（24）（25）により、
（25）
① Ｂ＜Ｃ＞Ａ　＆　Ｂ＝Ａ＋１
といふ「順番」を、
① Ａ＜Ｂ＜Ｃ
といふ「順序」で読まうとしても、
① Ｂ＜Ｃ＞Ａ　＆　Ｂ＝Ａ＋１
に対して、「括弧」を、加へることは、出来ない。
然るに、
（26）
① Ｂ＜Ｃ＞Ａ　＆　Ｂ＝Ａ＋１
といふ「順番」を、
① Ａ＜Ｂ＜Ｃ
といふ「順序」で読む場合は、
① Ｂ←Ａ
に関しては、
① 右から、左へ、返る。
一方で、
① Ｂ→Ｃ
に関しては、
① 左から、右に、返る。
ことになる。
従って、
（17）（25）（26）により、
（27）
①「与へらた順番」が、
１　３　４　２
２　３　１　４
２　３　４　１
２　４　１　３
２　４　３　１
３　１　４　２
３　２　４　１
３　４　２　１
３　４　１　２
４　２　３　１
のやうに、
① Ｂ＜Ｃ＞Ａ　＆　Ｂ＝Ａ＋１
といふ「順番」を含む場合は、
①「与へられた順番」に対して、「返り点・括弧」を、加へることは、出来ない。
（28）
例へば、
① ｄｏｎ’ｔ　Ｅｎｇｌｉｓｈ　ｓｐｅａｋ　Ｉ　ａｔ　ａｌｌ.
① ２　４　３　１　５　６.
といふ「順番」を、「返り点・括弧」を用ゐて、
① Ｉ　ｄｏｎ’ｔ　ｓｐｅａｋ　Ｅｎｇｌｉｓｈ　ａｔ　ａｌｌ.
① １　２　３　４　５　６.
といふ「順序」に「並び替へる（ソートする）」ことは、出来ない。
従って、
（29）
① ２　３　４　１　５　６
① １　３　４　５　２　６　７
① １　２　４　５　６　３　７　８
といふ「順番」等を、「返り点・括弧」を用ゐて、
① １　２　３　４　５　６
① １　２　３　４　５　６　７
① １　２　３　４　５　６　７　８
といふ「順序」に「並び替へる（ソートする）」ことは、出来ない。
（30）
① ６＜７　２　３　４　１　５
① ７＜８　１　３　４　５　２　６
① ８＜９　１　２　４　５　６　３　７
といふ「順番」等を、「返り点・括弧」を用ゐて、
① １　２　３　４　５　６　７
① １　２　３　４　５　６　７　８
① １　２　３　４　５　６　７　８　９
といふ「順序」に「並び替へる（ソートする）」ことは、出来ない。
然るに、
（31）
4Ｐ4＝４×３×２×１＝２４個
から、
１　２　３　４
並びに、
１　３　４　２
２　３　１　４
２　３　４　１
２　４　１　３
２　４　３　１
３　１　４　２
３　２　４　１
３　４　２　１
３　４　１　２
４　２　３　１
を除いた「残り（補集合）」が、
１　２　４　３
１　３　２　４
１　４　２　３
１　４　３　２
２　１　３　４
２　１　４　３
３　１　２　４
３　２　１　４
４　１　２　３
４　１　３　２
４　２　１　３
４　３　１　２
４　３　２　１
であるため、これらの「１３個」の「順番」は、
① Ｂ＜Ｃ＞Ａ　＆　Ｂ＝Ａ＋１
といふ「順番」を含んでいないものの、これらの「返り点・括弧」は、（32）である。
（32）

（33）
１　２　４　３
１　３　２　４
１　４　２　３
１　４　３　２
２　１　３　４
２　１　４　３
３　１　２　４
３　２　１　４
４　１　２　３
４　１　３　２
４　２　１　３
４　３　１　２
４　３　２　１
といふ「順番（四桁）」を、
１　２　３　４　５　８　６　７
１　２　３　６　４　５　７　８
１　２　３　８　４　５　６　７
１　２　３　８　４　７　５　６
１　４　２　３　５　６　７　８
１　４　２　３　５　８　６　７
１　６　２　３　４　５　７　８
１　６　２　５　３　４　７　８
１　８　２　３　４　５　６　７
１　８　２　３　４　７　５　６
１　８　２　５　３　４　６　７
１　８　２　７　３　４　５　６
１　８　２　７　３　６　４　５
といふ「順番（八桁）」に「書き換へ」た際の、「返り点・括弧」は、（34）である。
（34）

（35）
（27）でも述べた通り、
１　３　４　２
２　３　１　４
２　３　４　１
２　４　１　３
２　４　３　１
３　１　４　２
３　２　４　１
３　４　２　１
３　４　１　２
４　２　３　１
といふ「順番」に付く「それ」は、「返り点」ではないものの、敢へて、「それ」を加へた「結果」が、（36）である。
（36）

然るに、
（37）
二　三　一　
二　三　一　
二　三　四　一
二　下　一　上
二　三　一
二　三レ　一　
二　三　一　
三　二　四　一
二　三　一レ
二　三　一
下　二　上　一
といふ「返り点」は、有り得ない。
（38）
二　三レ　一　
に関しては、「二つの返り点がいっしょになるのは、一とレ、上とレ、甲とレ、天とレの四つだけである（志村和久、漢文はやわかり、１８頁）。」であるため、
二　三レ
を含む、
二　三レ　一　
は、「返り点」ではなく、
二　下　一　上
下　二　上　一
に関しては、「一・二点をはさんで返る時は上・中・下点（志村和久、漢文早わかり、1982年、２０頁）。」であるため、
二　下　一
下　二　上　一
を含む、
二　下　一　上
下　二　上　一
は、「返り点」ではない。
従って、
（38）により、
（39）

といふ、「白話（中国語）訓読」の「それ」は、実際には、「返り点」ではない。
従って、
（23）（27）（39）により、
（40）
吃了多酒。
只管要纏擾我。
ＱＵＥＭ　ＬＩＢＲＵＭ　ＬＥＧＩＳ？
のやうな「白話文（中国語）」や「ラテン語」に対しては、「返り点・括弧」を用ゐて、「訓読」することが、出来ない。
（41）
Ａｒｅ〔ｙｏｕ　ｒｅａｄｉｎｇ（ｔｈｅ　ｂｏｏｋ）〕⇒
〔ｙｏｕ　（ｔｈｅ　ｂｏｏｋ）ｒｅａｄｉｎｇ〕Ａｒｅ＝
〔あなたは（件の本を）読んで〕ゐるか ： 三　二　一。
に対する、
Ｗｈａｔ（ｂｏｏｋ〔ａｒｅ［ｙｏｕ）〕ｒｅａｄｉｎｇ］⇒
（〔［ｙｏｕ）Ｗｈａｔ〕ｂｏｏｋｒｅａｄｉｎｇ］ａｒｅ＝
（〔［あなたは）何の〕本を読んで］ゐるか ： 二　三　五　一　四。
のやうな「英文（Ｗｈ移動）」も、「返り点・括弧」を用ゐて、「訓読」することが、出来ない。
（42）
汝所（読）為（何本）邪 ⇒
汝の（読む）所は（何の本）為るか。
は、もちろん、「返り点・括弧」を用ゐて、「訓読」することが出来る。
（43）
読漢文学漢字＝漢文を読み漢字学ぶ。
に対して、
二　一　四　三
といふ「返り点」を加へるならば、
二→三
となるものの、もちろん、正しくは、
二　一　二　一
である。
ｃｆ.

従って、
（44）
初学者に対しては、「返り点」とは、「下から、上へ返る」からこそ「返り点」である。
といふことを、最初に、教へるべきである。
従って、
（45）
二　三　一
四　二　三　一
下　二　上　一
二　四　一　三
二　下　一　上
といふ「返り点」は有り得ない。
といふことを、最初に、教へるべきである。
平成２７年１０月３１日、毛利太。

「括弧」が無いなら「返り点」も無い。

（01）
「返り点」とは、「縦書き」であれば、「下から上へ返る、返り点」であって、それ故、
「返り点」とは、「横書き」であれば、「右から左へ返る、返り点」である。
従って、
（01）により、
（02）
「返り点」とは、「横書き」であれば、「右から左へ返る、返り点」であって、それ故、
「返り点」とは、「横書き」であれば、「左から右へ返る、返り点」ではない。
従って、
（02）により、
（03）
β ： ２←１
α ： ３←２
ε ： ３←２←１
のやうな「順序」でなければ、「返り点」は付かない。
従って、
（03）により、
（04）
α ： １　３　２
β ： ２　１　３
γ ： ２　３　１
δ ： ３　１　２
ε ： ３　２　１
であれば、
α ： 囗　３　２
β ： ２　１　囗
γ ： ２　囗　１
δ ： ３　囗　２
ε ： ３　２　１
とした場合、「返り点」は、「囗の位置」には、付かない。
然るに、
（05）
γ ： ２　囗　１
といふ「順番」に付く「返り点」は、
① 二　囗　一
である。
然るに、
（06）
① 二　囗　一
に於いて、
① 「最初に」読まれる「それ」を、「＃」とすると、
① 二　＃　一
である。
ｃｆ.

従って、
（06）により、
（07）
① 二　囗　一
といふ「返り点」を、
① ２　３　１
の「順」で読まうとすれば、その場合は、
① 二　三　一
とせざるを得ない。
然るに、
（08）
① 二　三　一
であれば、
① 二→三　
であるため、「左から右」へ「返ってゐる」。
従って、
（02）（08）により、
（09）
① 二　三　一
といふ「返り点」は、存在しない。
従って、
（07）（08）（09）により、
（10）
「返り点」は、
① ２　３　１
といふ「順番」に、付くことが、出来ない。
（11）
② 二　三　囗　一
であれば、
② 二　三　＃　一
である。
然るに、
（12）
② 二　三　＃　一
であれば、
② ＃→一→二→三
従って、
（11）（12）により、
（13）
② 二　三　囗　一
といふ「それ」を、
② ２　３　４　１
の「順」で読まうとすれば、その場合は、
② 二　三　四　一
とせざるを得ない。
然るに、
（14）
② 二　三　四　一
であれば、
② 二→三→四　
であるため、「左から右」へ「返ってゐる」。
従って、
（02）（14）により、
（15）
② 二　三　四　一
といふ「返り点」は、存在しない。
従って、
（13）（14）（15）により、
（16）
「返り点」は、
② ２　３　４　１
といふ「順番」に、付くことが、出来ない。
（17）
③ 二　囗　三　一
であれば、
③ 二　＃　三　一
である。
然るに、
（18）
③ 二　＃　三　一
であれば、
③ ＃→一→二→三
従って、
（17）（18）により、
（19）
③ 二　囗　三　一
といふ「それ」を、
③ ２　４　３　１
の「順」で読まうとすれば、その場合は、
③ 二　四　三　一
とせざるを得ない。
然るに、
（20）
③ 二　四　三　一
であれば、
③ 二→三
であるため、「左から右」へ「返ってゐる」。
従って、
（02）（20）により、
（21）
③ 二　四　三　一
といふ「返り点」は、存在しない。
但し、
（22）

然るに、
（23）
〔説明〕二つの返り点がいっしょになるのは、一とレ、上とレ、甲とレ、天とレの四つだけである（志村和久、漢文早やわかり、1982年、１８頁）。
従って、
（21）（22）（23）により、
（24）
③ 二　四　三　一
③ 二　三レ　一
といふ「返り点」は、存在しない。
従って、
（19）～（24）により、
（25）
「返り点」は、
③ ２　４　３　１
といふ「順番」に、付くことが、出来ない。
従って、
（10）（16）（25）により、
（26）
「返り点」は、
① ２　３　１
② ２　３　４　１
③ ２　４　３　１
といふ「順番」に、付くことが、出来ない。
然るに、
（27）
④ 中　二　一　下　二　一　上
であれば、
④ 六　二　一　七　四　三　五
然るに、
（28）
④ 六　二　一　七　四　三　五
であれば、
④ 二→三
④ 四→五
④ 六→七
である。
然るに、
（29）
④ 中　二　一　下　二　一　上
であるため、
④ 中　二　一　下　四　三　上
であっても、
④ 中　二　一　下
④ 下　四　三　上
の「二　一」と、「四　三」は、別々の、異なる「一二点」である。
加へて、
（30）
④ 四　五
であっても、
④ 二　上
は、一方は、「一二点」であって、一方は「上下点」である。
従って、
（27）～（30）により、
（31）
④ 中　二　一　下　二　一　上
④ 六　二　一　七　四　三　五
であれば、
④ 中→下
④ 六→七
であるため、「左から右」へ「返ってゐる」。
従って、
（02）（31）により、
（32）
④ 中　二　一　下　二　一　上
といふ「返り点」は、存在しない。
従って、
（27）（31）（32）により、
（33）
「返り点」は、
④ ６　２　１　７　４　３　５
といふ「順番」に、付くことが、出来ない。
（10）（16）（25）（33）により、
（34）
「返り点」は、
① ２　３　１
② ２　３　４　１
③ ２　４　３　１
④ ６　２　１　７　４　３　５
といふ「順番」に、付くことが、出来ない。
然るに、
（35）
① ２　３　１
② ２　３　１
③ ２　４　１
④ ６　７　５
といふ「それ」は、
① Ｌ＜Ｍ＞Ｎ　＆　Ｌ＝Ｎ＋１
② Ｌ＜Ｍ＞Ｎ　＆　Ｌ＝Ｎ＋１
③ Ｌ＜Ｍ＞Ｎ　＆　Ｌ＝Ｎ＋１
④ Ｌ＜Ｍ＞Ｎ　＆　Ｌ＝Ｎ＋１
といふ「不等式」を、満たしてゐる。
然るに、
（36）
① ２→３
② ２→３
③ ２→４
④ ６→５
従って、
（35）（36）により、
（37）
① ２→３
② ２→３
③ ２→４
④ ６→５
といふ、「左から右へ」が生じる「所以」は、
①  Ｌ＜Ｍ＞Ｎ　＆　Ｌ＝Ｎ＋１
といふ「不等式」に、他ならない。
然るに、
（38）
① ２（３〔１）〕
② ２（３〔４［１）〕］
③ ２（４［３〔１）〕］
④ ６〔２（１）７［４（３）５〕］
に於いて、
① ２（　）⇒（　）１
① ３〔　〕⇒〔　〕３
② ２（　）⇒（　）１
② ３〔　〕⇒〔　〕３
② ４［　］⇒［　］４
③ ２（　）⇒（　）１
③ ３〔　〕⇒〔　〕３
③ ４［　］⇒［　］４
④ ２（　）⇒（　）１
④ ４（　）⇒（　）４
④ ６〔　〕⇒〔　〕６
④ ７［　］⇒［　］７
とすると、
① （〔１）２〕３
② （〔［１）２〕３］４
③ （［〔１）２〕３］４
④ 〔（１）２［（３）４５〕６］７
然るに、
（39）
① （　）
② 〔　〕
に於いて、
② が有る場合は、② の中には、一つ以上の ① が有って、
① の中には、① が無いならば、その時に限って、「括弧」とする。
従って、
（39）により、
（40）
① （ 〔　） 〕
② （ 〔 ［　） 〕 ］
③ （ ［ 〔　） 〕 ］
④ 〔（　）［ （　） 〕 ］
は、「括弧」ではない。
従って、
（34）（37）（38）（40）により、
（41）
① Ｌ＜Ｍ＞Ｎ　＆　Ｌ＝Ｎ＋１
といふ「順番」を含む、
① ２　３　１
② ２　３　４　１
③ ２　４　３　１
④ ６　２　１　７　４　３　５
といふ「順番」に対して、「返り点・括弧」は、付くことが、出来ない。
然るに、
（42）
① Ｌ＜Ｍ＞Ｎ　＆　Ｌ＝Ｎ＋１
ではなく、
① Ｌ＜Ｍ＜Ｎ
であれば、例へば、
① １＜２＜３
であるため、初めから、「返り点」は「不用」である。
（43）
① Ｌ＜Ｍ＞Ｎ　＆　Ｌ＝Ｎ＋１
ではなく、
① Ｌ＞Ｍ＜Ｎ
であれば、例へば、
① ２＞１＜３
であるため、
① ２（１）３⇒
① （１）２３＝
① １　２　３。
（44）
① Ｌ＜Ｍ＞Ｎ　＆　Ｌ＝Ｎ＋１
ではなく、
② Ｌ＞Ｍ＞Ｎ
であれば、例へば、
② ４＞３＞２
であるため、
② ４〔３（２）〕⇒
② 〔（２）３〕４＝
② ２　３　４。
従って、
（42）（43）（44）より、
（45）
① ３　１　２
② ２　１　３　４
③ ４　３　１　２
④ ２　１　７　４　３　５　６
のやうに、
① Ｌ＜Ｍ＞Ｎ　＆　Ｌ＝Ｎ＋１
ではなければ、
① ３（１　２）
② ２（１）３　４
③ ４〔３（１　２）〕
④ ２（１）７〔４（３）５　６〕
のやうに、「括弧」を付けることが出来、尚且つ、
① ３（１　２）
② ２（１）３　４
③ ４〔３（１　２）〕
④ ２（１）７〔４（３）５　６〕
に対する「返り点」は、
① 二　一
② レ
③ レ　二　一
④ レ　二　レ　一
である。
ｃｆ.

従って、
（41）（45）により、
（46）
① Ｌ＜Ｍ＞Ｎ　＆　Ｌ＝Ｎ＋１
といふ「順番」を含む、
① ２　３　１
② ２　３　４　１
③ ２　４　３　１
④ ６　２　１　７　４　３　５
といふ「順番」に対して、「返り点・括弧」は、付くことが、出来ない一方で、
① Ｌ＜Ｍ＞Ｎ　＆　Ｌ＝Ｎ＋１
といふ「順番」を含まない、
① ３　１　２
② ２　１　３　４
③ ４　３　１　２
④ ２　１　７　４　３　５　６
といふ「順番」に対しては、「返り点・括弧」を、付けることが、出来る。
然るに、
（47）
「返り点」とは、「縦書き」であれば、「下から上へ返る、返り点」であって、それ故、
「返り点」とは、「横書き」であれば、「右から左へ返る、返り点」である。
とするならば、以上の「理屈」は、
① 一　二　三　四　五　六　七　八　九　十　・ ・ ・ ・ ・
② 上　中　下
だけでなく、
① 一　二　三　四　五　六　七　八　九　十　・ ・ ・ ・ ・
② 上　中　下
③ 甲　乙　丙　丁　戊　己　庚　辛　壬　癸
④ 天　地　人
⑤ レ
⑥ 一レ　上レ　甲レ　天レ
といふ「返り点」と、
① （　）
② 〔　〕
③ ［　］
④ ｛　｝
といふ「括弧」に対しても、当てはまらざるを得ない。
従って、
（46）（47）により、
（48）
「与えられた順番」が、
① Ｌ＜Ｍ＞Ｎ　＆　Ｌ＝Ｎ＋１
といふ「順番」を含まないのであれば、その時に限って、「返り点・括弧」は、それらの「順番」を、
① １＜２＜３＜４＜５＜６＜７＜８＜９＜１０ ・ ・ ・ ・ ・
といふ「順番（昇べき順）」に「並び替へる（ソートする）」ことが、出来る。
（49）
「返り点、括弧、順列（一昨日の記事）」も、併せてお読み下さい。
（50）
漢語における語順は、国語と大きく違っているところがある。その補足構造における語順は、国語とは全く反対である（鈴木直治著、中国語と漢文、1975年、２９６頁）。
然るに、
（51）
① 我不常読英語。
に於いて、
① 我＝主語
① 常＝修飾語（副詞）
① 英＝修飾語（形容詞）
従って、
（50）（51）により、
（52）
① 我不常読英語＝
① 我不〔常読（英語）〕⇒
② 我〔常（英語）読〕不＝
② 我常には英語を読ま不。
といふ「漢文訓読」が、「可能」となる「所以」は、
① 我不常読英語。
といふ「漢文」には、
① 我不〔常読（英語）〕。
といふ、
①「補足構造」が有って、
② 我常には英語を読ま不。
といふ「和文」には、
② 我〔常（英語）読〕不。
といふ、
②「補足構造」が有るからである。
従って、
（53）
「支那の言語や文字を研究するのに、漢文と支那語の様な区別を設けてゐるのは、世界中、日本だけで、支那はもとより、ヨーロッパやアメリカで支那学を研究するにも、そんな意味のない
区別など夢にも考へてゐない。西洋人が支那のことを研究するには、何よりも先き、支那の現代の言葉を学び、現代人の書く文章を読み、それから次第に順序を追うて、古い言葉で書いた書物を読んで、支那民族の文化の深淵を理解する。アメリカの大学で支那のことを研究する学生は、最初の年に現代語学現代文学を学び、次の年に歴史の書物を読み経書を習ふさうである（勉誠出版、「訓読」論、2008年、５７頁）。さすがに、現在においては、「漢文訓読法」でなければ、日本人だけでなく、中国人も中国古典は理解できない、などという倒錯した主張をなす者はいなくなった。今から考えてみれば「漢文訓読法」派は単に現代中国語ができなかっただけのことではなかったか、そのようにさえ思えてくる（勉誠出版、「訓読」論、2008年、２頁）。
といふこととは、「関係」なく、例へば、
① 我不常読英語＝
① 我不〔常読（英語）〕⇒
② 我〔常（英語）読〕不＝
② 我常には英語を読ま不。
といふ「漢文訓読」に於ける、
① 〔 （　） 〕
といふ「括弧」は、
① 我不常読英語。
といふ「漢文」の「補足構造（シンタックス）」を、表してゐる。
然るに、
（54）
① 我三〔常二（英一）〕。
に於いて、
① 三＝不
① 二＝読
① 一＝語
とすれば、
① 我三〔常二（英一）〕⇒
② 我〔常（英一）二〕三＝
② 我〔常（英語）読〕不＝
② 我常には英語を読ま不。
従って、
（54）により、
（55）
① 三〔二（一）〕
といふ「返り点・括弧」は、
① 我不〔常読（英語）〕。
といふ「漢文」の「補足構造（シンタックス）」を、表してゐる。
然るに、
（56）
例へば、「新釈漢文大系 全120巻（別巻1） - 明治書院」には、
① 一　二　三　四　五　六　七　八　九　十　・ ・ ・ ・ ・
② 上　中　下
③ 甲　乙　丙　丁　戊　己　庚　辛　壬　癸
④ 天　地　人
⑤ レ
⑥ 一レ　上レ　甲レ　天レ
が、付けられてゐる。
然るに、
（57）
例へば、

従って、
（58）
例へば、「新釈漢文大系 全120巻（別巻1） - 明治書院」の中に、
① 使籍誠不以畜妻子憂飢寒乱心有銭財以済医薬。
といふ「漢文」が有ったとして、その「返り点」が、
① 人　乙　下　二　一　中　上　甲レ　二　一　地　天
であったなら、その「返り点」を、
① 人　丙　下　二　一　中　上　乙　甲　二　一　地　天
とした上で、次に、
① 人｛丙［下〔二（一）中（上）〕乙（甲）］二（一）地（天）｝
とすれば、
① 人｛丙［下〔二（一）中（上）〕乙（甲）］二（一）地（天）｝
といふ「返り点・括弧」は、
① 使籍誠不以畜妻子憂飢寒乱心有銭財以済医薬。
といふ「漢文」の「補足構造（シンタックス）」を、表してゐる。
従って、
（58）により、
（59）
例へば、「新釈漢文大系 全120巻（別巻1） - 明治書院」には、「返り点」といふ「形」で、「漢文」の「補足構造（シンタックス）」が、示されてゐる。
従って、
（60）
アメリカの大学で支那のことを研究する学生は、最初の年に現代語学現代文学を学び、次の年に歴史の書物を読み経書を習ふさうである（勉誠出版、「訓読」論、2008年、５７頁）。
とのことである、亜米利加の學生が、例へば、
① 使籍誠不以畜妻子憂飢寒乱心有銭財以済医薬。
といふ「漢文」の「補足構造（シンタックス）」を知りたいの場合は、「返り点・括弧」を、知ってゐるべきである。
然るに、
（61）
博士課程後期に六年間在学して訓読が達者になった中国の某君があるとき言った。「自分たちは古典を中国音で音読することができる。しかし、往々にして自ら欺くことがあり、助詞などいいかげんに飛ばして読むことがある。しかし日本式の訓読では、「欲」「将」「当」「謂」などの字が、どこま管到して（かかって）いるか、どの字から上に返って読むか、一字もいいかげんにできず正確に読まなければならない」と、訓読が一字もいやしくしないことに感心していた。これによれば倉石武四郎氏が、訓読は助詞の類を正確に読まないと非難していたが、それは誤りで、訓読こそ中国音で音読するよりも正確な読み方なのである（原田種成、私の漢文 講義、1995年、２７頁）。
従って、
（61）により、
（62）
中國の學生であっても、例へば、
① 使籍誠不以畜妻子憂飢寒乱心有銭財以済医薬。
といふ「漢文」の「補足構造（シンタックス）」を知りたいのであれば、その場合は、「返り点・括弧」を、知ってゐるべきである。
平成２７年１０月２０日、毛利太。

返り点、括弧、順列。

― 「１０月１６日の記事」を、書き換へます。―
（01）
「未」「將」「當」「應」「宜」「須」「猶」「盍」などの諸字は、一字でありながら、最初、副詞に読み、次に動詞あるいは助動詞と読むのが慣例となっている。― 中略 ―
「未」は「いまダ～ず」とよみ、「まだ～しない」の意で、「尚不」と同じである（中沢希男・澁谷玲子、漢文訓読の基礎、1985年、９０頁）。
従って、
（01）により、
（02）
＿未嘗有不可対人言者耳＝
尚不嘗有不可対人言者耳＝
尚不〈嘗有｛不［可〔対（人）言〕］者｝〉耳⇒
尚〈嘗｛［〔（人）対言〕可］不者｝有〉不耳＝
尚だ嘗て人に対して言ふ可から不る者有ら不るのみ。
然るに、
（03）
尚丙〈嘗乙｛下［中〔二（一）上〕］甲｝〉者。
に於いて、
丙＝不
乙＝有
下＝不
中＝可
二＝対
一＝人
上＝言
甲＝者
であれば、
尚丙〈嘗乙｛下［中〔二（一）上〕］甲｝〉者⇒
尚〈嘗｛［〔（一）二上〕中］下甲｝乙〉丙者＝
尚〈嘗｛［〔（人）対言〕可］不者｝有〉不耳＝
尚だ嘗て人に対して言ふ可から不る者有ら不るのみ。
従って、
（02）（03）により、
（04）
尚不嘗有不可対人言者耳＝
尚だ嘗て人に対して言ふ可から不る者有ら不るのみ。
といふ「漢文」に付く「返り点」は、
丙　乙　下　中　二　一　上　甲
である。
然るに、
（05）

従って、
（04）（05）により、
（06）
例へば、
① 下　中　レ　二　レ　一　上
② 二　レ　一レ
③ レ
④ レ　レ
⑤ レ　レ　レ
⑥ 二　一レ　二　一
⑦ 乙　下　二　レ　一レ　上レ　レ　甲レ
といふ「返り点（レ点有り）」は、
① 丙　乙　下　中　二　一　上　甲
② 下　二　一　中　上
③ 二　一
④ 三　二　一
⑤ 四　三　二　一
⑥ 四　三　二　一
⑦ 人　丙　下　二　一　中　上　乙　甲　二　一　地　天
といふ「返り点（レ点無し）」に、「置き換へ」ることが、出来る。
従って、
（06）により、
（07）
② 上　中　下
④ 天　地　人
といふ、それぞれの「三組」で「不足」が生じない限り、
① 一　二　三　四　五　六　七　八　九　十　・ ・ ・ ・ ・
② 上　中　下
③ 甲　乙　丙　丁　戊　己　庚　辛　壬　癸
④ 天　地　人
⑤ レ
⑥ 一レ　上レ　甲レ　天レ
といふ「返り点」で表すことが出来る「順番」の「集合」は、
① 一　二　三　四　五　六　七　八　九　十　・ ・ ・ ・ ・
② 上　中　下
③ 甲　乙　丙　丁　戊　己　庚　辛　壬　癸
④ 天　地　人
といふ「返り点」で表すことが出来る「順番」の「集合」に、等しい。
従って、
（07）により、
（08）
① （　）
② 〔　〕
③ ［　］
④ ｛　｝
で表すことが出来ない「順番」の「集合」が「集合Β」であるとして、
① 一　二　三　四　五　六　七　八　九　十　・ ・ ・ ・ ・
② 上　中　下
③ 甲　乙　丙　丁　戊　己　庚　辛　壬　癸
④ 天　地　人
で表すことが出来ない「順番」の「集合」も「集合Β」であるならば、「Βの補集合」は、
① （　）
② 〔　〕
③ ［　］
④ ｛　｝
といふ「括弧」、並びに、
① 一　二　三　四　五　六　七　八　九　十　・ ・ ・ ・ ・
② 上　中　下
③ 甲　乙　丙　丁　戊　己　庚　辛　壬　癸
④ 天　地　人
⑤ レ
⑥ 一レ　上レ　甲レ　天レ
といふ「返り点」で、表すことが出来る「順番」の『集合』に、等しい。
従って、
（07）（08）により、
（09）
① 一　二　三　四　五　六　七　八　九　十　・ ・ ・ ・ ・
② 上　中　下
③ 甲　乙　丙　丁　戊　己　庚　辛　壬　癸
④ 天　地　人
⑤ レ
⑥ 一レ　上レ　甲レ　天レ
といふ「返り点」で表すことが出来る「順番」の『集合』は、
① （　）
② 〔　〕
③ ［　］
④ ｛　｝
といふ「括弧」で表すことが出来る「順番」の『集合』に等しい。
といふ「定理」を証明するためには、
① （　）
② 〔　〕
③ ［　］
④ ｛　｝
で表すことが出来ない「順番」の「集合」が、
① 一　二　三　四　五　六　七　八　九　十　・ ・ ・ ・ ・
② 上　中　下
③ 甲　乙　丙　丁　戊　己　庚　辛　壬　癸
④ 天　地　人
で表すことが出来ない「順番」の「集合」に等しい。
といふことを示せば、「十分」である。
然るに、
（10）
「返り点」とは、「縦書き」であれば、「下から、上へ返る、返り点」であって、それ故、
「返り点」とは、「横書き」であれば、「右から、左へ返る、返り点」であって、それ故、
「返り点」とは、「横書き」であれば、「左から、右へ返る、返り点」ではない。
従って、
（10）により、
（11）
β ： ２←１
α ： ３←２
ε ： ３←２←１
の「順」でなければ、「返り点」は付かない。
従って、
（11）により、
（12）
α ： １　３　２
β ： ２　１　３
γ ： ２　３　１
δ ： ３　１　２
ε ： ３　２　１
であれば、
α ： 囗　３　２
β ： ２　１　囗
γ ： ２　囗　１
δ ： ３　囗　２
ε ： ３　２　１
とした場合、「返り点」は、「囗の位置」には、付かない。
従って、
（12）により、
（13）
α ： １　３　２
β ： ２　１　３
γ ： ２　３　１
δ ： ３　１　２
ε ： ３　２　１
に付く「一二点」は、
α ： 囗　二　一
β ： 二　一　囗
γ ： 二　囗　一
δ ： 二　囗　一
ε ： 三　二　一
である。
然るに、
（14）
α ： 囗　二　一
β ： 二　一　囗
γ ： 二　囗　一
δ ： 二　囗　一
ε ： 三　二　一
に於いて、「一番最初」に読まれる「囗」を、「＃」に「置き換へ」ると、
α ： ＃　二　一
β ： 二　一　囗
γ ： 二　＃　一
δ ： 二　＃　一
ε ： 三　二　一
ｃｆ.

然るに、
（15）
α ： ＃　二　一
γ ： 二　＃　一
δ ： 二　＃　一
に於いて、「＃」を、「一番最初」に読むためには、「＃＝〇」として、　
α ： 〇　二　一
γ ： 二　〇　一
δ ： 二　〇　一
とする「必要」がある。
然るに、
（16）
α ： 〇　二　一
γ ： 二　〇　一
δ ： 二　〇　一
といふ「順番」は、
α ： 一　三　二
γ ： 三　一　二
δ ： 三　一　二
といふ「順番」、すなはち、
α ： １　３　２
γ ： ３　１　２
δ ： ３　１　２
に、他ならない。
然るに、
（17）
β ： 二　一　囗
ε ： 三　二　一
の場合は、もちろん、
β ： ２　１　３
ε ： ３　２　１
である。
従って、
（16）（17）により、
（18）
α ： １　３　２
β ： ２　１　３
γ ： ３　１　２
δ ： ３　１　２
ε ： ３　２　１
である。
従って、
（13）（18）により、
（19）
γ ： ２　３　１
であって、
γ ： ３　１　２
であるものの、
γ ： ２　３　１
γ ： ３　１　２
は、もちろん、「矛盾」である。
従って、
（11）～（19）により、
（20）
「返り点」とは、「横書き」であれば、「右から、左へ返る、返り点」であって、
「返り点」とは、「横書き」であれば、「左から、右へ返る、返り点」ではない。
とする限り、
α ： １　３　２
β ： ２　１　３
γ ： ２　３　１
δ ： ３　１　２
ε ： ３　２　１
に於いて、
γ ： ２　３　１
といふ「順番」に対応する「返り点」は、存在しない。
然るに、
（21）

従って、
（20）（21）により、
（22）
「理屈」の上でも、「事実」の上でも、
γ ： ２　３　１
といふ「順番」に対応する「返り点」は、存在しない。
然るに、
（23）
α ： １　３　２
β ： ２　１　３
γ ： ２　３　１
δ ： ３　１　２
ε ： ３　２　１
といふ「五つの順番」の内の、
γ ： ２　３　１
に対して、
① （　）
② 〔　〕
を加へると、
γ ： ２（３〔１）〕
然るに、
（24）
γ ： ２（３〔１）〕
に於いて、
γ ： ２（　）⇒（　）２
γ ： ３〔　〕⇒〔　〕３
とするならば、
γ ： ２（３〔１）〕⇒
γ ： （〔１）２〕３＝１２３。
然るに、
（25）
① （　）
② 〔　〕
に於いて、
② が有る場合は、② の中には、一つ以上の ① が有って、
① の中には、① が無いならば、その時に限って、「括弧」とする。
然るに、
（26）
γ ： ２（３〔１）〕
の「それ」は、
γ ： （ 〔　） 〕
であるため、「括弧」ではない。
従って、
（24）（25）（26）により、
（27）
γ ： ２（３〔１）〕⇒
γ ： （〔１）２〕３＝１２３。
といふ「ソート（並び替へ）」は、「括弧」による「ソート（並び替へ）」ではない。
従って、
（27）により、
（28）
α ： １　３　２
β ： ２　１　３
γ ： ２　３　１
δ ： ３　１　２
ε ： ３　２　１
といふ「五つの順番」の内、
γ ： ２　３　１
に関しては、「括弧」による「ソート（並び替へ）」を行ふことが、出来ない。
然るに、
（25）により、
（29）
α ： １　３（２）
β ： ２（１　３）
γ ：
δ ： ３（１　２）
ε ： ３〔２（１）〕
の場合は、「四つ」とも、「括弧」である。
従って、
（28）（29）により、
（30）
α ： １　３　２
β ： ２　１　３
γ ： ２　３　１
δ ： ３　１　２
ε ： ３　２　１
といふ「五つの順番」の内、
γ ： ２　３　１
だけは、「括弧」による「ソート（並び替へ）」を行ふことが、出来ない。
従って、
（20）（30）により、
（31）
「3Ｐ3（順列）」、すなはち、
１　２　３
１　３　２
２　１　３
２　３　１
３　１　２
３　２　１
といふ「六つの順番」から、
１＜２＜３
を除いた、
α ： １　３　２
β ： ２　１　３
γ ： ２　３　１
δ ： ３　１　２
ε ： ３　２　１
といふ「五つの順番」の内、
γ ： ２　３　１
だけは、「返り点・括弧」による「ソート（並び替へ）」を行ふことが、出来ない。
従って、
（31）により、
（32）
Ｌ＜Ｍ＞Ｎ　＆　Ｌ＝Ｎ＋１
に於いて、
Ｌ ＝２
Ｍ＝３
Ｎ ＝１
である時、「返り点・括弧」は、
Ｌ＜Ｍ＞Ｎ
を、
Ｎ＜Ｌ＜Ｍ
といふ「順番」に、「並び替へる（ソートする）」ことが出来ない。
（33）
初めから、
１＜２＜３＜４
である、
１　２　３　４
を除いて、
１　２　４　３
１　３　２　４
１　３　４　２
１　４　２　３
１　４　３　２
２　１　３　４
２　１　４　３
２　３　１　４
２　３　４　１
２　４　１　３
２　４　３　１
３　１　２　４
３　１　４　２
３　２　１　４
３　２　４　１
３　４　２　１
３　４　１　２
４　１　２　３
４　１　３　２
４　２　１　３
４　２　３　１
４　３　１　２
４　３　２　１
に対して、「括弧」を加へると、
１　２　４（３）
１　３（２）４
１　３（４〔２）〕
１　４（２　３）
１　４〔３（２）〕
２（１）３　４
２（１）４（３）
２（３〔１）〕４
２（３〔４［１）〕］
２（４〔１）３〕
２（４［３〔１）〕］
３（１　２）４
３（１　４〔２）〕
３〔２（１）〕４
３〔２（４［１）〕］
３〔４［２（１）〕］
３（４〔１　２）〕
４（１　２　３）
４〔１　３（２）〕
４〔２（１）３〕
４［２（３〔１）〕］
４〔３（１　２）〕
４［３〔２（１）〕］
（34）
① （　）
② 〔　〕
③ ［　］
に於いて、
③ が有る場合は、③ の中には、一つ以上の ② が有って、
② が有る場合は、② の中には、一つ以上の ① が有って、
① の中には、① が無いならば、その時に限って、「括弧」とする。
従って、
（33）（34）により、
（35）
１　３（４〔２）〕
２（３〔１）４〕
２（３〔４［１）〕］
２（４〔１）３〕
２（４［３〔１）〕］
３〔１（４［２）〕］
３〔２（４［１）〕］
３〔４［２（１）〕］
３（４〔１　２）〕
４［２（３〔１）〕］
に於ける、
　　　（　〔　）〕
　（　〔　）　〕
　（　〔　［　）〕］
　（　〔　）　〕
　（　［　〔　）〕］
　〔　（　［　）〕］
　〔　（　［　）〕］
　〔　［　（　）〕］
　（　〔　　　）〕
　［　（　〔　）〕］
は、「括弧」ではない。
従って、
（35）により、
（36）
１　３　４　２
２　３　１　４
２　３　４　１
２　４　１　３
２　４　３　１
３　１　４　２
３　２　４　１
３　４　２　１
３　４　１　２
４　２　３　１
といふ「順番」に対しては、
① （　）
② 〔　〕
③ ［　］
といふ「括弧」を用ゐた、「ソート（並び替へ）」を行ふことが、出来ない。
然るに、
（37）
例へば、
１　３　４　２
であれば、
１　３＜４＞２
であるため、
Ｌ ＝３
Ｍ＝４
Ｎ ＝２
である時、
１　３　４　２
といふ「順番」は、
Ｌ＜Ｍ＞Ｎ　＆　Ｌ＝Ｎ＋１
といふ「順番」を、含んでゐる。
（38）
例へば、
３　１　４　２
であれば、
３＞１＜４＞２
であるため、
Ｌ ＝３
Ｍ＝４
Ｎ ＝２
である時、
３　１　４　２
といふ「順番」は、
Ｌ＜Ｍ＞Ｎ　＆　Ｌ＝Ｎ＋１
といふ「順番」を、含んでゐる。
従って、
（37）（38）により、
（39）
１　３　４　２
２　３　１　４
２　３　４　１
２　４　１　３
２　４　３　１
３　１　４　２
３　２　４　１
３　４　２　１
３　４　１　２
４　２　３　１
といふ「順番」は、
１＜３＜４＞２
２＜３＞１＜４
２＜３＜４＞１
２＜４＞１＜３
２＜４＞３＞１
３＞１＜４＞２
３＞２＜４＞１
３＜４＞２＞１
３＜４＞１＜２
４＞２＜３＞１
であるが故に、「１０個」とも、
Ｌ＜Ｍ＞Ｎ　＆　Ｌ＝Ｎ＋１
といふ「順番」を、含んでゐる。
然るに、
（40）
１　２　４　３
１　３　２　４
１　４　２　３
１　４　３　２
２　１　３　４
２　１　４　３
３　１　２　４
３　２　１　４
４　１　２　３
４　１　３　２
４　２　１　３
４　３　１　２
４　３　２　１
の場合は、
１＜２＜４＞３
１＜３＞２＜４
１＜４＞２＜３
１＞４＞３＜２
２＞１＜３＜４
２＞１＜４＞３
３＞１＜２＜４
３＞２＞１＜４
４＞１＜２＜３
４＞１＜３＞２
４＞２＞１＜３
４＞３＞１＜２
４＞３＞２＞１
であるため、「１３個」とも、
Ｌ＜Ｍ＞Ｎ　＆　Ｌ＝Ｎ＋１
といふ「順番」を含んでゐない。
従って、
（33）～（40）により、
（41）
「順列（4Ｐ4）」から、
１＜２＜３＜４
を除いた「順番」を、
１　２　４　３
１　３　２　４
１　４　２　３
１　４　３　２
２　１　３　４
２　１　４　３
３　１　２　４
３　２　１　４
４　１　２　３
４　１　３　２
４　２　１　３
４　３　１　２
４　３　２　１
といふ「集合Α」と、
１　３　４　２
２　３　１　４
２　３　４　１
２　４　１　３
２　４　３　１
３　１　４　２
３　２　４　１
３　４　２　１
３　４　１　２
４　２　３　１
といふ「集合Β」に、分けた場合、
①「集合Α」は、「括弧」を用ゐた、「ソート（並び替へ）」を行ふことが、出来、尚且つ、
①「集合Α」は、「Ｌ＜Ｍ＞Ｎ　＆　Ｌ＝Ｎ＋１」といふ「順番」を含んでゐない。
②「集合Β」は、「括弧」を用ゐた、「ソート（並び替へ）」を行ふことが、出来ずに、尚且つ、
②「集合Β」は、「Ｌ＜Ｍ＞Ｎ　＆　Ｌ＝Ｎ＋１」といふ「順番」を含んでゐる。
従って、
（41）により、
（42）
「順列（4Ｐ4）」から、
１＜２＜３＜４
を除いた場合、「与えられた順番」が、「Ｌ＜Ｍ＞Ｎ　＆　Ｌ＝Ｎ＋１」といふ「順番」を含んでゐないならば、その時に限って、その「順番」は、「括弧」を用ゐた「ソート（並び替
へ）」が、可能である。
然るに、
（43）
「集合Α」の「返り点」は、
１　３　４　２ ： 二　三　一
２　３　１　４ ： 二　三　一
２　３　４　１ ： 二　三　四　一
２　４　１　３ ： 二　四　一　三
２　４　３　１ ： 二　三レ　一
３　１　４　２ ： 二　三　一
３　２　４　１ ： 三　二　四　一
３　４　２　１ ： 二　三　一レ
３　４　１　２ ： 二　三　一
４　２　３　１ ： 四　二　三　一
である。
（44）
「集合Β」の「それ」は、
１　３　４　２ ： 二　三　一
２　３　１　４ ： 二　三　一
２　３　４　１ ： 二　三　四　一
２　４　１　３ ： 二　四　一　三
２　４　３　１ ： 二　三レ　一
３　１　４　２ ： 二　三　一
３　２　４　１ ： 三　二　四　一
３　４　２　１ ： 二　三　一レ
３　４　１　２ ： 二　三　一
４　２　３　１ ： 四　二　三　一
である。
然るに、
（45）
「返り点」は、「横書き」であれば、「左へ返る点」であって、「右へ返る点」ではない。が故に、
１　２　４　３ ： レ
１　３　２　４ ： レ
１　４　２　３ ： 二　一
１　４　３　２ ： レ　レ
２　１　３　４ ： レ
２　１　４　３ ： レ　レ
３　１　２　４ ： 二　一
３　２　１　４ ： レ　レ
４　１　２　３ ： 二　一
４　１　３　２ ： 二　一レ
４　２　１　３ ： 二　レ　一
４　３　１　２ ： レ　二　一
４　３　２　１ ： レ　レ　レ
の「それ」は、「返り点」である。一方で、
１　３　４　２ ： 二　三　一
２　３　１　４ ： 二　三　一
２　３　４　１ ： 二　三　四　一
２　４　１　３ ： 二　四　一　三
２　４　３　１ ： 二　三レ　一
３　１　４　２ ： 二　三　一
３　２　４　１ ： 三　二　四　一
３　４　２　１ ： 二　三　一レ
３　４　１　２ ： 二　三　一
４　２　３　１ ： 四　二　三　一
の「それ」は、「返り点」ではない。
従って、
（41）～（45）により、
（46）
「順列（4Ｐ4）」から、
１＜２＜３＜４
を除いた場合、「与えられた順番」が、「Ｌ＜Ｍ＞Ｎ　＆　Ｌ＝Ｎ＋１」といふ「順番」を含んでゐないならば、その時に限って、その「順番」は、「返り点・括弧」を用ゐた「ソート
（並び替へ）」が、可能である。
従って、
（31）（32）（46）により、
（47）
１＜２＜３
１　３　２
２　１　３
２　３　１
３　１　２
３　２　１
１＜２＜３＜４
１　２　４　３
１　３　２　４
１　３　４　２
１　４　２　３
１　４　３　２
２　１　３　４
２　１　４　３
２　３　１　４
２　３　４　１
２　４　１　３
２　４　３　１
３　１　２　４
３　１　４　２
３　２　１　４
３　２　４　１
３　４　２　１
３　４　１　２
４　１　２　３
４　１　３　２
４　２　１　３
４　２　３　１
４　３　１　２
４　３　２　１
から、
１＜２＜３
１＜２＜３＜４
を除ゐた場合、
Ｌ＜Ｍ＞Ｎ　＆　Ｌ＝Ｎ＋１
Ｌ＜Ｍ＞Ｎ
を含む「順番」を含まないならば、その時に限って、「返り点・括弧」による、「並び替へ（ソート）」が、可能になる。
従って、
（47）により、
（48）
２　３　１
２　３　４　１
のやうな「順番」の場合は、「括弧」を用ゐた、「ソート（並び替へ）」を行ふことが、出来ない。
然るに、
（49）
２　３　１
２　３　４　１
に於いて、さうであれば、
３　４　２
３　４　５　２
に於いても、さうであり、それ故、
１　３　４　２
１　３　４　５　２
のやうな「順番」の場合も、「括弧」を用ゐた、「ソート（並び替へ）」を行ふことが、出来ない。
然るに、
（50）
１　３　４　２
１　３　４　５　２
に於いて、さうであれば、
１１　１３　１４　１２
１１　１３　１４　１５　１２
のやうな「順番」の場合も、「括弧」を用ゐた、「ソート（並び替へ）」を行ふことが、出来ない。
従って、
（25）（34）（48）（49）（50）により、
（51）
① （　）
② 〔　〕
③ ［　］
④ ｛　｝
に於いて、
④ が有る場合は、④ の中には、一つ以上の ③ が有って、
③ が有る場合は、③ の中には、一つ以上の ② が有って、
② が有る場合は、② の中には、一つ以上の ① が有って、
① の中には、① が無いならば、その時に限って、「括弧」である。
とするとき、
Ｌ＜Ｍ＞Ｍ　＆　Ｌ＝Ｎ＋１　
といふ「順番」を含む「順番」であれば、その時に限って、「括弧」を用ゐた、「ソート（並び替へ）」を行ふことは、出来ない。
然るに、
（52）
２０　１　２　１２　９　５　３　４　８　６　７　１１　１０　１５　１３　１４　１６　１９　１７　１８＝
２０｛１　２　１２［９〔５（３　４）８（６　７）〕１１（１０）］１５（１３　１４）１６　１９（１７　１８）｝⇒
｛１　２　［〔（３　４）５（６　７）８〕９（１０）１１］１２（１３　１４）１５１６　（１７　１８）１９｝２０＝
１　２　３　４　５　６　７　８　９　１０　１１　１２　１３　１４　１５　１６　１７　１８　１９　２０
従って、
（51）（52）により、
（53）
２０＞１＜２＜１２＞９＞５＞３＜４＜８＞６＜７＜１１＞１０＜１５＞１３＜１４＜１６＜１９＞１７＜１８
といふ「順番」は、
Ｌ＜Ｍ＞Ｍ　＆　Ｌ＝Ｎ＋１
といふ「順番」を含まない。
然るに、
（54）
２０｛１　２　１２［９〔５（３　４）８（６　７）〕１１（１０）］１５（１３　１４）１６　１９（１７　１８）｝
に於いて、
１　２　３　６　１３　１６　１７
の場合は、「そのまま、上から下（左から右）へ読む」ため、「返り点」は、固より、「不要」である。
従って、
（54）により、
（55）
「返り点」を考へる場合に、「１　２　３　６　１３　１６　１７」は「不要」であるため、
２０｛１　２　１２［９〔５（３　４）８（６　７）〕１１（１０）］１５（１３　１４）１６　１９（１７　１８）｝⇒
２０｛１２［９〔５（４）８（７）〕１１（１０）］１５（１４）１９（１８）｝⇒
１３｛８［５〔２（１）４（３）〕７（６）］１０（９）１２（１１）｝。
とすれば、
１３　８　５　２　１　４　３　７　６　１０　９　１２　１１
といふ「順番」は、「返り点」に、相当する。
然るに、
（56）
２０　１　２　１２　９　５　３　４　８　６　７　１１　１０　１５　１３　１４　１６　１９　１７　１８
といふ「順番」に対して、
十三　八　五　二　一　四　三　七　六　十　九　十二　十一
といふ「一二点」だけを加へるならば、
使＝20＝十三
籍＝１
誠＝２
不＝12＝八
以＝９ ＝五
畜＝５ ＝二
妻＝３
子＝４ ＝一
憂＝８ ＝四
飢＝６
寒＝７ ＝三
乱＝11＝七
心＝10＝六
有＝15＝十
銭＝13
財＝14＝九
以＝16
済＝19＝十二
医＝17
薬＝18＝十一
然るに、
（57）
一・二点をはさんで返る時は上・中・下点。
上・中・下点をはさんで返る時は甲・乙点。
甲・乙点をはさんで返る時は天・地（天・地・人）点である。
（志村和久、漢文早わかり、1982年、２０頁）
従って、
（56）（57）により、
（58）
使＝20＝人
籍＝１
誠＝２
不＝12＝丙
以＝９ ＝下
畜＝５ ＝二
妻＝３
子＝４ ＝一
憂＝８ ＝中
飢＝６
寒＝７ ＝上
乱＝11＝乙
心＝10＝甲
有＝15＝二
銭＝13
財＝14＝一
以＝16
済＝19＝地
医＝17
薬＝18＝天
ｃｆ.

従って、
（52）～（58）により、
（59）
① 使籍誠不以畜妻子憂飢寒乱心有銭財以済医薬＝
① 使｛籍誠不［以〔畜（妻子）憂（飢寒）〕乱（心）］有（銭財）以済（医薬）｝⇒
①｛籍誠［〔（妻子）畜（飢寒）憂〕以（心）乱］不（銭財）有以（医薬）済｝使＝
①｛籍をして誠に［〔（妻子を）畜ひ（飢寒を）憂ふるを〕以て（心を）乱さ］不（銭財）有りて以て（医薬を）済さ｝使む。
に付く「返り点」は、
① 人　丙　下　二　一　中　上　乙　甲　二　一　地　天
である。
然るに、
（60）
使＝20＝人
籍＝１
誠＝２
不＝12＝丙
以＝９ ＝下
畜＝５ ＝二
妻＝３
子＝４ ＝一
憂＝８ ＝中
飢＝６
寒＝７ ＝上
乱＝11＝乙
心＝10＝甲
有＝15＝二
銭＝13
財＝14＝一
以＝16
済＝19＝地
医＝17
薬＝18＝天
に於いて、
　使＝20＝人
　が
　不＝12＝丙
　と、
　以＝９＝下
　の間に移動した場合が、（61）である。
（61）
籍＝１
誠＝２
不＝12＝丙
使＝20＝人
以＝９ ＝下
畜＝５ ＝二
妻＝３
子＝４ ＝一
憂＝８ ＝中
飢＝６
寒＝７ ＝上
乱＝11＝乙
心＝10＝甲
有＝15＝二
銭＝13
財＝14＝一
以＝16
済＝19＝地
医＝17
薬＝18＝天
然るに、
（51）（57）（61）により、
（62）
丙　人　乙
であれば、
甲・乙点が、天・地点をはさんでゐる。
が故に、「返り点」として、「矛盾」するし、
１２＜２０＞１１
であるため、すなはち、
Ｌ＜Ｍ＞Ｍ　＆　Ｌ＝Ｎ＋１
であるため、「括弧」は無い。
（63）
使＝20＝人
籍＝１
誠＝２
不＝12＝丙
以＝９ ＝下
畜＝５ ＝二
妻＝３
子＝４ ＝一
憂＝８ ＝中
飢＝６
寒＝７ ＝上
乱＝11＝乙
心＝10＝甲
有＝15＝二
銭＝13
財＝14＝一
以＝16
済＝19＝地
医＝17
薬＝18＝天
に於いて、
　心＝10＝甲
　が
　畜＝５＝二
　と、
　子＝４＝一
　の間に移動した場合が、（64）である
（64）
使＝20＝人
籍＝１
誠＝２
不＝12＝丙
以＝９ ＝下
畜＝５ ＝二
妻＝３
心＝10＝甲
子＝４ ＝一
憂＝８ ＝中
飢＝６
寒＝７ ＝上
乱＝11＝乙
有＝15＝二
銭＝13
財＝14＝一
以＝16
済＝19＝地
医＝17
薬＝18＝天
然るに、
（51）（57）（64）により、
（65）
二　甲　一
であれば、
一・二点が、甲・乙点をはさんでゐる。
が故に、「矛盾」するし、
５＜１０＞４
であるため、すなはち、
Ｌ＜Ｍ＞Ｍ　＆　Ｌ＝Ｎ＋１
であるため、「括弧」は無い。
（66）
使＝20＝人
籍＝１
誠＝２
不＝12＝丙
以＝９ ＝下
畜＝５ ＝二
妻＝３
子＝４ ＝一
憂＝８ ＝中
飢＝６
寒＝７ ＝上
乱＝11＝乙
心＝10＝甲
有＝15＝二
銭＝13
財＝14＝一
以＝16
済＝19＝地
医＝17
薬＝18＝天
に於いて、
　心＝10＝甲
　が
　有＝15＝二
　と、
　財＝14＝一
　の間に移動した場合が、（67）である。
（67）
使＝20＝人
籍＝１
誠＝２
不＝12＝丙
以＝９ ＝下
畜＝５ ＝二
妻＝３
子＝４ ＝一
憂＝８ ＝中
飢＝６
寒＝７ ＝上
乱＝11＝乙
有＝15＝二
銭＝13
心＝10＝甲
財＝14＝一
以＝16
済＝19＝地
医＝17
薬＝18＝天
然るに、
（51）（57）（67）により、
（68）
乙　二　甲　一
であれば、
一・二点が、甲・乙点をはさんでゐる。
が故に、「矛盾」するし、
１１＜１５＞１０＞１４
であるため、すなはち、
Ｌ＜Ｍ＞Ｍ　＆　Ｌ＝Ｎ＋１
であるため、「括弧」は無い。
（69）
使＝20＝人
籍＝１
誠＝２
不＝12＝丙
以＝９ ＝下
畜＝５ ＝二
妻＝３
子＝４ ＝一
憂＝８ ＝中
飢＝６
寒＝７ ＝上
乱＝11＝乙
心＝10＝甲
有＝15＝二
銭＝13
財＝14＝一
以＝16
済＝19＝地
医＝17
薬＝18＝天
に於いて、
　不＝12＝丙
　が
　有＝15＝二
　と、
　銭＝13
　財＝14＝一
　の間に移動した場合が、（70）である。
（70）
使＝20＝人
籍＝１
誠＝２
以＝９ ＝下
畜＝５ ＝二
妻＝３
子＝４ ＝一
憂＝８ ＝中
飢＝６
寒＝７ ＝上
乱＝11＝乙
心＝10＝甲
有＝15＝二
不＝12＝丙
銭＝13
財＝14＝一
以＝16
済＝19＝地
医＝17
薬＝18＝天
然るに、
（57）により、
（58）
不＝12＝丙
銭＝13
であれば、
　有＝15＝二
　不＝12
　銭＝13
　財＝14＝一
となって、「丙」は、消えてしまふ。
（71）
２０｛１　２　１２［９〔５（３　４）８（６　７）〕１１（１０）］１５（１３　１４）１６　１９（１７　１８）｝
に対して、
２０〈１　２　１９｛１２［９〔５（３　４）８（６　７）〕１１（１０）］１５（１３　１４）１６　１７　１８｝〉
であるため、
（　）
〔　〕
［　］
｛　｝
に対して、
〈　〉を加へれば、「返り点・括弧」は、
使＝20＝人
籍＝１
誠＝２
済＝19＝地
不＝12＝丙
以＝９ ＝下
畜＝５ ＝二
妻＝３
子＝４ ＝一
憂＝８ ＝中
飢＝６
寒＝７ ＝上
乱＝11＝乙
心＝10＝甲
有＝15＝二
銭＝13
財＝14＝一
以＝16
医＝17
薬＝18＝天
といふ「順番」を表すことが、出来る。
（72）
２０｛１　２　１２［９〔５（３　４）８（６　７）〕１１（１０）］１５（１３　１４）１９〔１７（１６）１８〕｝
であるため、「返り点・括弧」は、
使＝20＝人
籍＝１
誠＝２
不＝12＝丙
以＝９ ＝下
畜＝５ ＝二
妻＝３
子＝４ ＝一
憂＝８ ＝中
飢＝６
寒＝７ ＝上
乱＝11＝乙
心＝10＝甲
有＝15＝二
銭＝13
財＝14＝一
済＝19＝地
医＝17＝二
以＝16＝一
薬＝18＝天
といふ「順番」を表すことが、出来る。
（73）
使＝20＝人
籍＝１
誠＝２
不＝12＝丙
以＝９ ＝下
畜＝５ ＝二
妻＝３
子＝４ ＝一
憂＝８ ＝中
飢＝６
寒＝７ ＝上
乱＝11＝乙
心＝10＝甲
有＝15＝二
銭＝13
財＝14＝一
以＝16
済＝19＝地
医＝17
薬＝18＝天
に於いて、
　済＝19＝地
　が
　有＝15＝二
　と、
　銭＝13
　財＝14＝一
　の間に移動した場合が、（74）である。
（74）
使＝20＝人
籍＝１
誠＝２
不＝12＝丙
以＝９ ＝下
畜＝５ ＝二
妻＝３
子＝４ ＝一
憂＝８ ＝中
飢＝６
寒＝７ ＝上
乱＝11＝乙
心＝10＝甲
有＝15＝二
済＝19＝地
銭＝13
財＝14＝一
以＝16
医＝17
薬＝18＝天
然るに、
（51）（57）（74）により、
（75）
二　地　一
であれば、
一・二点が、天・地点をはさんでゐる。
が故に、「矛盾」するし、
１５＜１９＞１３・１４
であるため、すなはち、
Ｌ＜Ｍ＞Ｍ　＆　Ｌ＝Ｎ＋１
であるため、「括弧」は無い。といふ「意味」は、
２０｛１　２　１２［９〔５（３　４）８（６　７）〕１１（１０）］１５（１９〔１３　１４）１６　１７　１８〕｝⇒
｛１　２　［９〔（３　４）５（６　７）８〕（１０）１１］１２（〔１３　１４）１５１６　１７　１８〕１９｝２０。
に於ける、
１５（１９〔１３　１４）１６　１７　１８〕
といふ「部分」の、
（ 〔　） 〕
といふ「それ」が、「括弧」ではない。といふことに、他ならない。
（76）
使＝20＝人
籍＝１
誠＝２
不＝12＝丙
以＝９ ＝下
畜＝５ ＝二
妻＝３
子＝４ ＝一
憂＝８ ＝中
飢＝６
寒＝７ ＝上
乱＝11＝乙
心＝10＝甲
有＝15＝二
銭＝13
財＝14＝一
以＝16
済＝19＝地
医＝17
薬＝18＝天
に於いて、
　薬＝18＝天
　が
　有＝15＝二
　と、
　銭＝13
　財＝14＝一
　の間に移動した場合が、（77）である。
（77）
使＝20＝人
籍＝１
誠＝２
不＝12＝丙
以＝９ ＝下
畜＝５ ＝二
妻＝３
子＝４ ＝一
憂＝８ ＝中
飢＝６
寒＝７ ＝上
乱＝11＝乙
心＝10＝甲
有＝15＝二
薬＝18＝天
銭＝13
財＝14＝一
以＝16
済＝19＝地
医＝17
然るに、
（51）（57）（77）により、
（78）
二　天　一
であれば、
一・二点が、天・地点をはさんでゐる。
が故に、「矛盾」するし、
１５＜１８＞１３・１４
であるため、すなはち、
Ｌ＜Ｍ＞Ｍ　＆　Ｌ＝Ｎ＋１
であるため、「括弧」は無い。といふ「意味」は、
２０｛１　２　１２［９〔５（３　４）８（６　７）〕１１（１０）］１５（１８〔１３　１４）１６　１９［１７〕］｝⇒
｛１　２　１２［９〔５（３　４）８（６　７）〕１１（１０）］（〔１３　１４）１５１６　［１７〕１８］１９｝２０。
に於ける、
１５（１８〔１３　１４）１６　１９［１７〕］
といふの「部分」の
（ 〔　）［　〕 ］
といふ「それ」が、「括弧」ではない。といふことに、他ならない。
然るに、
（79）
使＝20＝囗
籍＝１
誠＝２
不＝12＝丙
以＝９ ＝下
畜＝５ ＝二
妻＝３
子＝４ ＝一
憂＝８ ＝中
飢＝６
寒＝７ ＝上
乱＝11＝乙
心＝10＝甲
済＝19＝人
有＝15＝二
銭＝13
財＝14＝一
以＝16
薬＝18＝地
医＝17＝天
であれば、
２０｛１　２　１２［９〔５（３　４）８（６　７）〕１１（１０）］１９〔１５（１３　１４）１６１８（１７）〕｝⇒　
｛１　２　［〔（３　４）５（６　７）８〕９（１０）１１］１２〔（１３　１４）１５１６（１７）１８〕１９｝２０。
であるため、
① （　）
② 〔　〕
③ ［　］
④ ｛　｝
については、「不足」しないものの、、
① 一　二　三　四　五　六　七　八　九　十　・ ・ ・ ・ ・
② 上　中　下
③ 甲　乙　丙　丁　戊　己　庚　辛　壬　癸
④ 天　地　人　囗
に於ける、
④ 囗　が、「不足」する。
従って、
（01）～（79）により、
（80）
① 一　二　三　四　五　六　七　八　九　十　・ ・ ・ ・ ・
② 上　中　下
③ 甲　乙　丙　丁　戊　己　庚　辛　壬　癸
④ 天　地　人
といふ「返り点」で表すことが出来る「順番」の「集合」、すなはち、
① 一　二　三　四　五　六　七　八　九　十　・ ・ ・ ・ ・
② 上　中　下
③ 甲　乙　丙　丁　戊　己　庚　辛　壬　癸
④ 天　地　人
⑤ レ
⑥ 一レ　上レ　甲レ　天レ
といふ「返り点」で表すことが出来る「順番」の「集合」と、
① （　）
② 〔　〕
③ ［　］
④ ｛　｝
で表すことが出来る「順番」の「集合」は、
② 上　中　下
④ 天　地　人
の、それぞれの「三つ」が「不足」しない限り、
④ ｛　｝
の次の、
⑤ 〈　〉
を「必要」としない限り、等しい。
要するに、
（81）
「返り点」は、「縦書き」であれば、「上へ返る点」であって、「下へ返る点」ではない。が故に、
「返り点」は、「横書き」であれば、「左へ返る点」であって、「右へ返る点」ではない。にも拘はらず、
Ｌ＜Ｍ＞Ｍ　＆　Ｌ＝Ｎ＋１
といふ「順番」を、「返り点」を用ゐて、
Ｎ＜Ｌ＜Ｍ
といふ「順番」に「ソートし（並び替へ）」ようとすると、「下へ返る、返る点」を、用ゐざるを得ず、それ故、「（返り点としての）反則」が生じ、その際に、「括弧」であれば、
二（三〔一）〕に於ける、（ 〔　） 〕のやうな、「（括弧としての）反則」が、生じることになる。
従って、
（82）
① 一　二　三　四　五　六　七　八　九　十　・ ・ ・ ・ ・
② 上　中　下
③ 甲　乙　丙　丁　戊　己　庚　辛　壬　癸
④ 天　地　人
⑤ レ
⑥ 一レ　上レ　甲レ　天レ
といふ「返り点」を、「下へ返る点」として、用ゐることが無いのであれば、その時に限って、
① （　）
② 〔　〕
③ ［　］
④ ｛　｝
といふ「括弧」が、表すことが出来る「順番」の「集合」と、
① 一　二　三　四　五　六　七　八　九　十　・ ・ ・ ・ ・
② 上　中　下
③ 甲　乙　丙　丁　戊　己　庚　辛　壬　癸
④ 天　地　人
⑤ レ
⑥ 一レ　上レ　甲レ　天レ
といふ「返り点」が、表すことが出来る「順番」の「集合」は、等しい。
Ｑ.Ｅ.Ｄ.
平成２７年１０月１７日、毛利太。
― 「熟語の場合」―
（83）
① 読（漢文）⇒
① （漢文）読＝
① （漢文を）読む。
に対して、
② 訓‐読（漢文）⇒
② （漢文）訓‐読＝
② （漢文を）訓‐読す。
従って、
（84）
① ３（１　２）⇒
① （１　２）３。
に対して、
② ３‐４（１　２）⇒
② （１　２）３‐４。
然るに、
（85）
② ３‐４　１　２
に於いて、
② Ｌ ＝３
② Ｍ＝４
② Ｎ ＝２
であれば、
② Ｌ＜Ｍ＞Ｎ　＆　Ｌ＝Ｎ＋１
である。
然るに、
（86）
②「訓読」のやうな、「二字熟語」は、
②「一語」と、見なす。
従って、
（87）
② 訓‐読（漢文）⇒
② （漢文）訓‐読＝
② （漢文を）訓‐読す。
の場合も、
① 読（漢文）⇒
① （漢文）読＝
① （漢文を）読む。
と同様に、
② ３（１　２）⇒
② （１　２）３。
であって、
② ３‐４（１　２）⇒
② （１　２）３‐４。
ではない。
ｃｆ.

従って、
（88）
② 訓‐読（漢文）。
の場合も、
② Ｌ＜Ｍ＞Ｎ　＆　Ｌ＝Ｎ＋１
ではない。
（89）
③ 先‐後‐生（三文字）
等も、「一語」と見なすため、
③ ３‐４‐５（１　２）⇒
③ （１　２）３‐４‐５。
とは、ならず、それ故、
③ Ｌ＜Ｍ＞Ｎ　＆　Ｌ＝Ｎ＋１
ではない。
― 「白話（中国語）」の場合 ―
（90）
例へば、「新釈漢文大系 全120巻（別巻1） - 明治書院」には、
① 一　二　三　四　五　六　七　八　九　十　・ ・ ・ ・ ・
② 上　中　下
③ 甲　乙　丙　丁　戊　己　庚　辛　壬　癸
④ 天　地　人
⑤ レ
⑥ 一レ　上レ　甲レ　天レ
が、付けられてゐる。
従って、
（82）（90）により、
（91）
「新釈漢文大系 全120巻（別巻1） - 明治書院」に対しては、
① （　）
② 〔　〕
③ ［　］
④ ｛　｝
⑤ 〈　〉
を、付けることが、出来る。
然るに、
（92）

然るに、
（93）
α ： ４　２＜３＞１　　（下　二　上　一）
β ： ２＜５　３＞１　４（二　五　三　一　四）
γ ： ２＜４　３＞１　　（二　三レ　一）
であるため、「括弧」を付けることが、出来ないし、
（94）
α ： 下　二　上　一
β ： 二　五　三　一　四
γ ： 二　三レ　一
の場合は、「上から下へ、返ってゐる」ため、「返り点」ではない。
従って、
（91）～（94）により、
（95）
「白話文（中国語）訓読」に於ける、
α ： 只管要纏擾我（下　二　上　一）。
β ： 端的看不出這婆子的本事来 　（二　五　三　一　四）。
β ： 西門慶促忙促急儧造不出床来（二　五　三　一　四）。
γ ： 吃了不多酒（二　三レ　一）。
といふ「語順」は、「漢文訓読」から見ると、「異常」である。　
従って、
（96）
「漢文」と「白話文（中国語）」は、甚だ、著しく、完全に、「異なる言語」であるとしか、思へない。
それ故、
（97）
私は中国語の勉強をお勧めします。私も中国語を勉強して白文を読むのが楽になりました（kiebine2007さん）。
といふことが、私には、信じられない。
平成２７年１０月１９日、毛利太。

返り点に対する「括弧」の用法（ｖｅｒ５．０ｂ）。

― １０月０８日の記事を、書き換へます。―
（01）
① （　）
② 〔　〕
③ ［　］
④ ｛　｝
⑤ 〈　〉
は、「括弧」である。
（02）
① （　）は　　  「小さな函」。
② 〔　〕は　　  「中位の函」。
③ ［　］は　 　 「大きな函」。
④ ｛　｝は  「より大きな函」。
⑤ 〈　〉は「さらに大きな函」。
に譬へることが、出来る。
（03）
①「小さな函」が、
②「中位の函」の中に、入ってゐる「状態」を、
② 〔 （　） 〕
とする。
然るに、
（04）
②「Ｍサイズの箱」が、
①「Ｓサイズの箱」の中に、入ることは、物理的に、有り得ない。
従って、
（02）（03）（04）により、
（05）
② 〔 （　） 〕
は、「函（括弧）」である。一方で、
① （ 〔　〕 ）
① （ 〔　） 〕
① 〔 （　〕 ）
のやうな「函（括弧）」は、有り得ない。
但し、
（06）
②  〔 （　） 〕
だけでなく、
②  〔 （　）（　） 〕
②  〔 （　）（　）（　） 〕
であっても、
①「小さな箱」が、
②「中位の箱」の中に、入ることには、変はりがない。
従って、
（01）～（06）により、
（07）
① （　）
② 〔　〕
③ ［　］
④ ｛　｝
⑤ 〈　〉
に於いて、
② の中に、一つ以上の ① が有って、
③ の中に、一つ以上の ② が有って、
④ の中に、一つ以上の ③ が有って、
⑤ の中に、一つ以上の ④ が有る。
ならば、「括弧」とする.
（08）
⑤ 〈　〉
で「不足」する場合は、
⑥ 《　》
⑦ 「　」
とする。
（09）
① 一　二　三　四　五　六　七　八　九　十　・ ・ ・ ・ ・
② 上　中　下
③ 甲　乙　丙　丁　戊　己　庚　辛　壬　癸
④ 天　地　人
⑤ レ
⑥ 一レ　上レ　甲レ　上レ
は、「返り点」である。
然るに、
（10）
例へば、
⑤ レ
⑤ レ　レ
⑥ 二　一レ　二　一
⑥ 二　レ　一レ
であれば、
⑤ 二　一
⑤ 三　二　一
⑥ 四　三　二　一
⑥ 下  二　一　中　上
と、「同じこと」である。
ｃｆ.

従って、
（09）（10）により、
（11）
以下では、
⑤ レ
⑥ 一レ　上レ　甲レ　上レ
を除いて、
① 一　二　三　四　五　六　七　八　九　十　・ ・ ・ ・ ・
② 上　中　下
③ 甲　乙　丙　丁　戊　己　庚　辛　壬　癸
④ 天　地　人
を、「返り点」とする。
（12）
一・二点をはさんで返る時は上・中・下点。
上・中・下点をはさんで返る時は甲・乙点。
甲・乙点をはさんで返る時は天・地（天・地・人）点である。
（志村和久、漢文早わかり、1982年、２０頁）
従って、
（12）により、
（13）
① 地　乙　下　二　一　上　甲　天
② 二　下　乙　地　天　甲　上　一
に於いて、
① は、「返り点」であるが、
② は、「返り点」ではない。
然るに、
（14）
① 地　乙　下　二　一　上　甲　天
② 二　下　乙　地　天　甲　上　一
を、「一二点」だけで表すと、
① 八　六　四　二　一　三　五　七
② 二　四　六　八　七　五　三　一
（15）
① 八　六　四　二　一　三　五　七
② 二　四　六　八　七　五　三　一
を、「数字」に置き換へると、
① ８　６　４　２　１　３　５　７
② ２　４　６　８　７　５　３　１
従って、
（13）（14）（15）により、
（16）
① 地　乙　下　二　一　上　甲　天
は、「返り点」であるが故に、「返り点」は、
① ８　６　４　２　１　３　５　７
といふ「順番」を、表すことが出来る。一方で、
② 二　下　乙　地　天　甲　上　一
は、「返り点」はないが故に、「返り点」は、
② ２　４　６　８　７　５　３　１
といふ「順番」を、表すことが、出来ない。
然るに、
（17）
① 八｛六［四〔二（一）三〕五］七｝
に於いて、
① 二（　）⇒（　）二
① 四〔　〕⇒〔　〕四
① 六［　］⇒［　］六
① 八｛　｝⇒｛　｝八
とすると、
① 八｛六［四〔二（一）三〕五］七｝⇒
① ｛［〔（一）二三〕四五］六七｝八。
従って、
（17）により、
（18）
① ｛ ［ 〔 （　） 〕 ］ ｝
といふ「括弧」も、
① 八　六　四　二　一　三　五　七
① ８　６　４　２　１　３　５　７
といふ「順番」を、表すことが出来る。
然るに、
（19）
② 二（四［六〈八「七《五｛三〔一）〕］｝〉》」
に於いて、
② 二（　）⇒（　）二
② 三〔　〕⇒〔　〕三
② 四［　］⇒［　］四
② 五｛　｝⇒｛　｝五
② 六〈　〉⇒〈　〉六
② 七《　》⇒《　》七
② 八「　」⇒「　」八
とすると、
② 二（四［六〈八「七《五｛三〔一）〕］｝〉》」⇒
②（［〈「《｛〔一）二〕三］四｝五〉六》七」八。
従って、
（19）により、
（20）
② （ ［ 〈 「 《 ｛ 〔  ） 〕 ］ ｝ 〉 》 」
といふ「それ」は、
② 二　四　六　八　七　五　三　一
② ２　４　６　８　７　５　３　１
といふ「順番」を、表すことが出来る。
然るに、
（07）（08）により、
（21）
① ｛ ［ 〔 （　） 〕 ］ ｝
② （ ［ 〈 「 《 ｛ 〔  ） 〕 ］ ｝ 〉 》 」
に於いて、
① は、「括弧」であるが、
② は、「括弧」ではない。
従って、
（18）（20）（21）により、
（22）
① ｛ ［ 〔 （　） 〕 ］ ｝
は、「括弧」であるが故に、「括弧」は、
① ８　６　４　２　１　３　５　７
といふ「順番」を、表すことが出来る。一方で、
② （ ［ 〈 「 《 ｛ 〔  ） 〕 ］ ｝ 〉 》 」
は、「括弧」はないが故に、「括弧」は、
② ２　４　６　８　７　５　３　１
といふ「順番」を、表すことが、出来ない。
従って、
（16）（22）により、
（23）
「返り点・括弧」は、
① ８＞６＞４＞２＞１＜３＜５＜７
といふ「順番」を、
① １＜２＜３＜４＜５＜６＜７＜８
といふ、「昇べき順」に、「並び替へる（ソート）」することは、可能である、一方で、
② ２＜４＜６＜８＞７＞５＞３＞１
といふ「順番」を、
① １＜２＜３＜４＜５＜６＜７＜８
といふ、「昇べき順」に、「並び替へる（ソート）」することは、可能ではない。
（24）
③ ２（３〔１）〕
に於いて、
③ ２（　）⇒（　）２
③ ３〔　〕⇒〔　〕３
とすると、
③ ２（３〔１）〕⇒
③ （〔１）２〕３。
然るに、
（07）により、
（25）
③ （ 〔　） 〕
は、「括弧」ではない。
従って、
（24）（25）により、
（26）
「括弧」は、
③ ２＜３＞１
といふ「順番」を、表すことが出来ない。
然るに、
（27）
③ 二　三　一
といふ「返り点」は、見たことがない。
言ひ換へると、
（28）
③ 注不意。
と書いて、
③ フチュウイ。
と読むやうな「漢文」は、見たことがない。

従って、
（24）～（28）により、
（29）
「返り点・括弧」は、
③ ２＜３＞１
といふ「順番」を、表すことが出来ない。
従って、
（23）（29）により、
（30）
「返り点・括弧」は、
③ ２＜３＞１
② ２＜４＜６＜８＞７＞５＞３＞１
といふ「順番」を、
① １＜２＜３
① １＜２＜３＜４＜５＜６＜７＜８
といふ、「昇べき順」に、「並び替へる（ソート）」することが、出来ない。
従って、
（30）により、
（31）
「返り点・括弧」は、
② Ｌ＜Ｍ＞Ｎ　＆　Ｌ＝Ｎ＋１
といふ「順番」を、
② Ｎ＜Ｌ＜Ｍ
といふ「順番」に、「並び替へる（ソートする）」ことが、出来ない。
従って、
（01）～（31）により、
（32）
「返り点」であれば、
① 一　二　三　四　五　六　七　八　九　十　・ ・ ・ ・ ・
② 上　中　下
③ 甲　乙　丙　丁　戊　己　庚　辛　壬　癸
④ 天　地　人
⑤ レ
⑥ 一レ　上レ　甲レ　上レ
といふ「６種類」の中の、
② 上　中　下
④ 天　地　人
に於いて、「不足」が生じない限り、
「括弧」であれば、
① （　）
② 〔　〕
③ ［　］
④ ｛　｝
⑤ 〈　〉
の次の、
⑥ 《　》
を「必要」としない限り、「返り点」と「括弧」は、「同じ順番」だけを、示すことが、出来る。
従って、
（32）により、
（33）
「返り点」が表すことが出来る「順番」の「集合」と、「括弧」が表すことが出来る「順番」の「集合」は、原理的に、等しい。
然るに、
（34）
④ 下　二　上　一
⑤ 二　五　三　一　四
⑥ 二　三レ　一
といふ「それ」は、
④ ４＞２＜３＞１
⑤ ２＜５＞３＞１＜４
⑥ ２＜４　３＞１
であるため、
④ ２＜３＞１　＆　２＝１＋１
⑤ ２＜５＞１　＆　２＝１＋１
⑥ ２＜４＞１　＆　２＝１＋１
といふ「順番」を、
④ １＜２＜３
⑤ １＜２＜５
⑥ １＜２＜４
といふ「順番」に、「並び替へる（ソートする）」ことが、出来る。
従って、
（31）（34）により、
（35）
④ 下　二　上　一
⑤ 二　五　三　一　四
⑥ 二　三レ　一
といふ、これらが、「返り点」であるとすると、「矛盾」する。
従って、
（35）により、
（36）
④ 下　二　上　一
⑤ 二　五　三　一　四
⑥ 二　三レ　一
は、「返り点」ではない。
従って、
（37）
④ 只‐管要纏我。
⑤ 端‐的看不出這婆‐子的本‐事来。
⑤ 西門慶促‐忙促－急儧‐造不出床来。
⑥ 吃了不多酒。
に付く、
④ 下　二　上　一
⑤ 二　五　三　一　四
⑥ 二　三レ　一
といふ「それ」は、「返り点」ではない。
然るに、
（38）
「返読」をするにも拘はらず、「返り点」を付けることが出来ない「漢文」は、存在しない。
従って、
（37）（38）により、
（39）
④ 只‐管要纏我。
⑤ 端‐的看不出這婆‐子的本‐事来。
⑤ 西門慶促‐忙促－急儧‐造不出床来。
⑥ 吃了不多酒。
は、「漢文」ではない。
ｃｆ.

加へて、
（40）
「原文（文言文）」で「曾子曰、敢問聖人之徳、無以加於孝乎（曾子曰く、敢えて問う　聖人の徳、以て孝に加うること無きか）」というところが、当時の口語訳（白話文）では「曾子問、孔子道聖人行的事、莫不更有強如孝道的勾當麽」となり、「孝莫大於厳父、厳父莫大於配天（孝は父を厳ぶより大なるは莫く、父を厳ぶは天に配するるよりは大なるは莫し）」というところが、白話訳では、 「孝的勾當都無大似的父親的、敬父親的勾當便似敬天一般」となっている。両者の違いは一目瞭然であろう（勉誠出版、続「訓読」論、2010年、３１２頁）。
然るに、
（41）
⑦ ゆく河の流れは絶えずして、しかももとの水にあらず（方丈記、冒頭）。
⑧ ゆく河の流れは絶えることがなく、しかももとの水ではない（現代語）。
に於いて、
⑦が分れば、
⑧が分からない。といふことは、有り得ない。
然るに、
（42）
⑦ 孝莫大於厳父、厳父莫大於配天。
⑧ 孝的勾當都無大似的父親的、敬父親的勾當便似敬天一般。
の場合は、
⑦は、分るのに、
⑧は、全く、分らない。
加へて、
（43）
しかし私が専門にしている中国明清の白話小説は必ずしも漢文訓読の方法では読めません。「白話」というのは話し言葉をもとにした書面語で、それを読むためには現代中国語の知識が必要になります。皆さんがよく知っているでしょう『三国志演義』・『水滸伝』・『西遊記』・『封神演義』などはみな白話で書かれている長編小説です。これらの小説を読むためには、まず現代中国語をしっかり学ばなければなりません（Ｗｅｂサイト：中川諭|大東文化大学）。簡潔を旨として作られた文言文とは異なり、話し言葉に基づく白話文は、本来訓読には適していない（実際、現在では白話文の訓読はほとんど行われていない）。しかし江戸時代、白話文は訓読されていた（勉誠出版、続「訓読」論、2010年、３３０頁）
従って、
（37）～（43）により、
（44）
④ 只‐管要纏我。
⑤ 端‐的看不出這婆‐子的本‐事来。
⑤ 西門慶促‐忙促－急儧‐造不出床来。
⑥ 吃了不多酒。
⑦ 孝的勾當都無大似的父親的、敬父親的勾當便似敬天一般。
といふ「白話（中国語）」は、「返り点」を付けることさへ「不可能」な、「漢文」とは、「全く異なる言語」である。と、せざるを得ない。
（45）
漢語における語順は、国語と大きく違っているところがある。その補足構造における語順は、国語とは全く反対である（鈴木直治著、中国語と漢文、1975年、２９６頁）。
然るに、
（46）
① 見〔釣（於濮水）〕⇔
① 〔（濮水に）釣るを〕見る。
の「語順」は、「全く反対」である。
従って、
（45）（46）により、
（47）
① 見〔釣（於濮水）〕⇔
① 〔（濮水に）釣るを〕見る。
に於ける、
① 〔 （　） 〕
① 〔 （　） 〕
といふ「括弧」は、「補足構造（シンタックス）」を、表してゐる。
従って、
（47）により、
（48）
① 我見〔荘子釣（於濮水）〕⇒
① 我〔荘子（於濮水）釣〕見＝
① 我〔荘子の（濮水に）釣るを〕見る。
に於ける、
① 〔 （　） 〕
① 〔 （　） 〕
といふ「括弧」は、「補足構造（シンタックス）」を、表してゐる。
然るに、
（49）
① 〔 （　） 〕は、
① 〔 （　） 〕に、等しい。
従って、
（48）（49）により、
（50）
① 我見〔荘子釣（於濮水）〕。
① 我〔荘子の（濮水に）釣るを〕見る。
に於ける、「シンタックス（括弧）」は、等しい。
然るに、
（51）
① 我見〔荘子釣（於濮水）〕。
① 我〔荘子の（濮水に）釣るを〕見る。
に於ける、「語順」は、等しくない。
従って、
（50）（51）により、
（52）
「シンタックス」が等しければ「語順」も等しい。とは、言へない。
従って、
（52）により、
（53）
「語順が等しい」ことは、「シンタックスが等しい」ための、「十分条件」ではあっても、「必要条件」ではない。
（54）
Ｗｈ移動 ：意味を導くための深層構造が必要だという説明の時に、一番最初に取り上げられたのは疑問詞が文頭にある疑問文でした。主語はともかく、目的語が動詞の直後ではなく、動詞の前しかも文の先頭にあるという事実を説明するためには、目的語である疑問詞がちゃんと動詞の直後にある深層構造を設定すればよいわけです（町田健、チョムスキー入門、2006年、１１７頁）。
然るに、
（55）
目的語である疑問詞（What）が、
ちゃんと動詞（doing）の直後に在る。
とすれば、
② are you doing What here＝
② are［you doing〔What（here）〕］⇒
③ ［you 〔（here）What〕doing］are＝
② ［あなたは〔（ここで）何を〕して］ゐる。
に於ける、「括弧（シンタックス）」は、
② ［ 〔 （　） 〕 ］
② ［ 〔 （　） 〕 ］
である。
従って、
（55）により、
（56）
② are you doing What here ?
② あなたはここで何をしてゐる。
に於いて、「語順」は異なるが、「括弧（シンタックス）」は、等しい。
然るに、
（57）
② are you doing What here ?
に於いて、
目的語である疑問詞（What）が、「Ｗｈ移動」をすると、
③ What（are［you doing〔here）〕］⇒
③ （［you〔here）What〕doing］are ＝
③ （［あなたは〔ここで）何を〕して］ゐる。
然るに、
（07）により、
（58）
③ （ ［ 〔　） 〕 ］
③ （ ［ 〔　） 〕 ］
は「括弧」ではない。
従って、
（55）～（58）により、
（59）
③ What are you doing  here ?
③ あなたはここで何をしてゐる。
の場合は、「語順」と「シンタックス」の、両方が、等しくない。
従って、
（54）～（59）により、
（60）
③ Wha are you doing here ?
③ あなたはここで何をしてゐる。
のいふ「英語」と「日本語」は、「深層構造」に於いて、「シンタックス」が、等しい？
（61）
動詞についての目的語は、その動詞の後に置かれるのが、漢語における基本的構造としての単語の配列のしかたである。また、漢語における介詞は、ほとんど、動詞から発達したものであって、その目的語も、その介詞の後に置かれるのが、その通例であるということができる。しかし、古代漢語においては、それらの目的語が、疑問詞である場合には、いずれも、その動詞・介詞の前に置かれる。このように漢語としての通常の語順を変えて、目的語の疑問詞を前置することは、疑問文において、その疑問の中心になっている疑問詞を、特に「強調」したものにちがいない（鈴木直治、中国語と漢文、３３４・３３５頁）。「排他的命題」を主張する「目的」が、「強調」に繋がり、「強調」しようといふ「意識」が、「疑問詞」の「前置」をプロモートする。
従って、
（61）により、
（62）
③ are you doing What here ?
に於ける、
③ What
が、「強調」を「目的」として「前置」され、尚且つ、その「前置」が、「固定」された「結果」が、
② What are you doing here ?
であると、思はれる。
（63）
今の日本の中学・中学では英語・数学・国語を主要３教科と呼んでいますが、戦前、旧制の中学では英語・数学・国語・漢文が主要４教科でした。漢文は国語とは独立した教科だったんですね。読解はもとより、復文（書き下し文から原文を復元）や作文もやるし、これだけ高度な学習内容でしたから、白文の読解もなんのそのでした。しかし戦後、漢文は国語の一部である古典分野の、そのまた片隅に追いやられてしまいました。漢文の得意な教師は少なく、漢文に興味を持つ生徒も少なく、おまけに最近は大学入試科目から漢文が消えつつあるので、みんないやいやながら学んでいます。内容もたいしたことはなく、学者先生が返り点と送り仮名をつけた文章をえっちらおっちら読む程度です（Ｗｅｂサイト：漢文入門）。
（64）
受験の際に、暗誦した、
① 欲は人の無き能はざる所なりと雖も、然れども多くして節せざれば未だ其の本心を失はざる者有らざるなり。
といふ「日本語」を思い出して、①を、
② 欲雖人之所不能無、然多而不節未有不失其本心者也。
といふ「漢文」に「復文」して、③のやうに、「括弧」で括ったとする。
③ 欲雖［人之所［不〔能（無）〕］、然多而不（節）未｛有［不〔失（其本心）〕者］｝也。
然るに、
（65）
③ 欲雖［人之所［不〔能（無）〕］、然多而不（節）未｛有［不〔失（其本心）〕者］｝也 ⇒
③ 欲は｛人の［〔（無き）能は〕不る］所なりと雖へども、然れども多くし而（節せ）不れば未だ｛［〔（其の本心を）失は〕不る者］有ら｝ざるなり。
に対応する「返り点」は、
③ 二　一レ　レ　レ、レ　レ　下　レ　二　一　上
である。
（66）
① 若し日本の中学生に必ず能く漢文を読まんと欲する者有らば則ち宜しく括弧を以て其の管到を学ぶ可し。
といふ「日本語」を思ひ浮かべて、①を、
② 若日本之中学生有必欲能読漢文者則宜以括弧学其管到。
といふ「漢文」に「復文」して、③のやうに、「括弧」で括ったとする。
③ 若日本之中学生有［必欲〔能読（漢文）〕者］則宜〔以（括弧）学（其管到）〕。
然るに、
（67）
③ 若日本之中学生有［必欲〔能読（漢文）〕者］則宜〔以（括弧）学（其管到）〕⇒
③ 若し日本の中学生に［必ず〔能く（漢文を）読まんと〕欲する者］有らば則ち宜しく〔（括弧を）以て（其の管到を）学〕可し。
に対応する「返り点」は、
③ 下　三　二　一　上　下　二　一　中　上
である。
然るに、
（68）
日本人が漢文を書く場合、漢文直訳体の日本語である漢文訓読は、有力な道具となり得る。まず頭のなかで漢文訓読体の日本語を思ひ浮かべ、それを漢文の語序にしたがって書く。次に、そうして書きあがった漢文を自分で訓読し、定型的な「句法」で訓読できない箇所はないか、返り点に無理はないか、などをチェックする。実際に漢詩・漢文を自分で書いてみればわかることだが、日本人が音読直読だけで純正漢文を書くことは、なかなかに難しい（そもそも漢文の音読直読ができる現代中国人でも、純正漢文が書ける者は少ない）。― 中略、― しかし専門家ではない一般知識人がそのレベルに達するには、大変な修練を必要とする。一方、漢文訓読を介して漢詩文を書くというメソッドならば、一般人でも修得が可能である（勉誠出版、「訓読」論、2008年、２６５・６頁）。
従って、
（63）～（68）により、
（69）
出来るだけ多くの「訓読」を暗誦して、その「暗誦」した「訓読」を、「復文」出来るやうにしてゐれば、その内に、平成の日本人であっても、江戸時代の日本人（一般の知識人）のやうに、「漢文」が書けるやうに、なるはずである。
然るに、
（70）
（青木）二百年前、正徳の昔に於て荻生徂徠は夙に道破した。漢学の授業法はまず支那語から取りかからねばならぬ。教うるに俗語を以てし、誦するに支那音を以てし、訳するに日本の俗語を以てし、決して和訓廻環の読み方をしてはならぬ。先ず零細な二字三字の短句から始めて、後には纏った書物を読ませる、斯くて支那語が熟達して支那人と同様になつてから、而る後段々と経子史集四部の書を読ませると云う風にすれば破竹の如しだ、是が最良の策だ（勉誠出版、「訓読」論、2008年、５６頁）。
（倉石）徂徠は、単に唐音を操るといふ様なことに満足せず、漢文を学ぶには先ず支那語からとりかり、支那の俗語をば支那語で暗誦させ、これを日本語の俗語に訳し、決して和訓の顚倒読みをしてはならない、始めは零細な二字三字の句から始めて、遂に纏った書物を読ます、支那語が支那人ほど熟達してから、古い書物を読ませば、破竹の勢いで進歩すると説いた（勉誠出版、「訓読」論、2008年、５６頁）。
（71）
予嘗為（蒙生）定（学問之方法）、先為（崎陽之学）、教以（俗語）、誦以（華音）、訳以（此方俚語）、絶不〔作（和訓廻環之読）〕、始以（零細者）、二字三字為（句）、後使［読〔成（書）者〕］｝、崎陽之学既成、乃始得〔為（中華人）〕、而後稍稍読（経子史集四部書）、勢如（破竹）、是最上乗也 ⇒
予嘗（蒙生）為（学問之方法）定、先（崎陽之学）為、教（俗語）以、誦（華音）以、訳（此方俚語）以、絶〔（和訓廻環之読〕作〕不、始（零細者）以、二字三字（句）為、後［〔（書）成者〕読］使、崎陽之学既成、乃始〔（中華人）為〕得、而後稍稍（経子史集四部書）読、勢（破竹）如、是最上乗也 ＝
予嘗て（蒙生の）為に（学問の方法を）定め、先ず（崎陽の学を）為し、教ふるに（俗語を）以てし、誦ずるに（華音を）以てし、訳するに（此の方の俚語を）以てし、絶へて〔（和訓廻環の読みを〕作さ〕ず、始めは（零細なる者を）以て、二字三字（句と）為し、後に［〔（書を）成す者を〕読ま］使めば、崎陽の学既に成り、乃ち始めて〔（中華の人）為る〕得、而る後に稍稍（経子史集四部書を）読まば、勢ひ（破竹の）如く、是れ最上の乗なり。
と読むのかどうかは、別にして、荻生徂徠自身は、この方法で、漢文を書くやうになったわけではない。はずである。
（72）
江戸に生まれる。幼くして学問に優れ、林春斎・林鳳岡に学んだ。しかし延宝7年（1679年）、当時館林藩主だった徳川綱吉の怒りにふれた父が江戸から放逐され、それによる蟄居にともない、14歳にして家族で母の故郷である上総国長柄郡本納村（現・茂原市）に移った[1]。 ここで主要な漢籍・和書・仏典を13年あまり独学し、のちの学問の基礎をつくったとされる（ウィキペディア）。
といふのであれば、荻生徂徠自身は、「漢文を学ぶ際に先ず支那語からとりかかってはゐない」。
加へて、
（73）
『漢語文法論（古代編）、1967年』、『漢語文法論（中古編）、1971年』の著者である、牛島徳次郎氏は、『中国古典の学び方、1977年、５９・６０頁』の中で、「学而優則仕（学びて優なれば則使ふ）」といふ、「返り点」さへ付かない、「これ以上簡単なそれが無いくらひに簡単の漢文（論語）」を、「中国語の知識」では、読めなかった。といふ風に、書かれてゐる。
ｃｆ.
学部の２年生でこの学習会に参加していた者たち二三人が、あるとき連れ立ってわたしの所に来、「学而優則仕」と書いた紙切れを示して、これはどういう意味ですかと、たずねた。どうしたのか、と聞くと、数日前の”記録新聞”に出て来て、そのときの「注釈」を聞きながら書くことは書いたが、意味がわからないので、という。そうか、これは『論語』の中の句で、「学んでゆとりがあったら官吏になる」ということだと説明した。それから１週間か十日ぐらいたったある夜、わたしは何か所かわからない箇所があった。あとで、みんなで読み合わせ、突き合わせて解読して行くうち、わたしが「次の一句が全然わからなかった。」というと、そばにいた二三人の学生が一斉に笑い出して、いった。「先生、そこはこの間、先生がぼくたちに教えてくれた”ｘｕｅ　ｅｒ　ｙｏｕ　ｚｅ　ｓｈｉ”ですよ！」これが私であり、あとで述べる「Ａ先生」なのである。漢字で書かれた”学而優則仕”を見ると、一応”ｘｕｅ　ｅｒ　ｙｏｕ　ｚｅ　ｓｈｉ”と発音することはする。
従って、
（72）（73）により、
（74）
「支那の言語や文字を研究するのに、漢文と支那語の様な区別を設けてゐるのは、世界中、日本だけで、支那はもとより、ヨーロッパやアメリカで支那学を研究するにも、そんな意味のない
区別など夢にも考へてゐない。西洋人が支那のことを研究するには、何よりも先き、支那の現代の言葉を学び、現代人の書く文章を読み、それから次第に順序を追うて、古い言葉で書いた書物を読んで、支那民族の文化の深淵を理解する。アメリカの大学で支那のことを研究する学生は、最初の年に現代語学現代文学を学び、次の年に歴史の書物を読み経書を習ふさうである（勉誠出版、「訓読」論、2008年、５７頁）。
といふ「主張」が、必ずしも、正しいとは、思へない。
（75）
先に示した、
④ 只‐管要纏我。
⑤ 端‐的看不出這婆‐子的本‐事来。
⑤ 西門慶促‐忙促－急儧‐造不出床来。
⑥ 吃了不多酒。
⑦ 孝的勾當都無大似的父親的、敬父親的勾當便似敬天一般。
を見る限り、「漢文」と「白話（中国語）」は、「英語」と「ラテン語」と同じくらひ、異なってゐるやうに思へるが、「ラテン語」を学ぶには、先ず、「英会話」を学ぶべきであると、考へる人は、ゐないはずである。
（76）
いづれにせよ、
アイヌ語や、ゲール語や、ピダハン語が、「消滅」してはならないのであれば、たとへ、「話し言葉」ではなくとも、明らかに、ユニークな「漢文訓読」は、「消滅」すべきではない。
（77）
漢字はことばではない、文字である。多くの文化人はそのことにふれずして、日本語論を語る。その結果、「訓読みは日本人の発明だ！」などという論調が蔓延してしまっているが、そ
んな日本と日本人の漢字礼讃傾向に、著者は真っ向から反論する書である（田中克彦、漢字が日本語をほろぼす、2011年、Ａｍａｚｏｎの書評？）。
（78）
このやうに、
During the past 160 years since Japan's chained doors were forced to open,
「漢字（漢文）」を亡ぼしたい人々が、常にゐる。
願はくは、彼等こそ、日本から、ゐなくならむ。
平成２７年１０月１１日、毛利太。

返り点に対する「括弧（函）」の用法Ⅲ。

（01）
① 我見〔荘子釣（於濮水）〕⇒
① 我〔荘子（於濮水）釣〕見＝
① 我〔荘子の（濮水に）釣るを〕見る。
然るに、
（02）
漢語における語順は、国語と大きく違っているところがある。その補足構造における語順は、国語とは全く反対である（鈴木直治著、中国語と漢文、1975年、２９６頁）。
従って、
（01）（02）により、
（03）
① 我見〔荘子釣（於濮水）〕。
① 我〔荘子の（濮水に）釣るを〕見る。
に於ける、
① 〔 （　） 〕
① 〔 （　） 〕
といふ「括弧」は、
① といふ「漢文の補足構造」を表してゐて、
① といふ「訓読の補足構造」を表してゐる。
然るに、
（04）
① 我見〔荘子釣（於濮水）〕。
① 我〔荘子の（濮水に）釣るを〕見る。
に於いて、
① 〔 （　） 〕と、
① 〔 （　） 〕は、等しい。
従って、
（03）（04）により、
（05）
① 我見〔荘子釣（於濮水）〕。
① 我〔荘子の（濮水に）釣るを〕見る。
に於いて、「語順」は異なるが、「補足構造（シンタックス）」は、等しい。
然るに、
（06）
② I saw〔her standing（there）〕⇒
② I 〔her（there）standing〕saw ＝
② 私は〔彼女が（そこに）立ってゐるのを〕見た。
（07）
③ You are［doing〔what（here）〕］⇒
③ You ［〔（here）what〕doing］are＝
③ あなたは［〔（ここで）何を〕して］ゐる。
従って、
（04）～（07）により、
（08）
① 我見荘子釣於濮水。
② I saw her standing there.
③ You are doing what here?
といふ「補足構造」は、それぞれ、
①    〔 （　） 〕
②    〔 （　） 〕
③ ［ 〔 （　） 〕 ］
を介して、
① 我荘子の濮水に釣るを見る。
② 私は彼女がそこに立ってゐるのを見た。
③ あなたは、ここで何をしてゐる。
といふ「補足構造」に、等しい。
然るに、
（09）
④ What（are［you doing〔here）〕］⇒
④ （［you〔here）What〕doing］are ＝
④ （［あなたは〔ここで）何を〕して］ゐる。
に於ける、
④ （ ［ 〔　） 〕 ］
④ （ ［ 〔　） 〕 ］
は、「括弧」とは、言へない。
従って、
（07）（08）（09）により、
（10）
③ You are doing what here? ⇒
③ あなたは、ここで何をしてゐる。
④ What are you doing here? ⇒
④ あなたは、ここで何をしてゐる。
に於いて、
③ であれば、「語順」は異なるが、「補足構造（シンタックス）」は、等しい。
④ であれば、「語順」は異なるし、「補足構造（シンタックス）」も、等しくない。
ｃｆ.
英語はWH句を義務的に移動しなくてはいけない言語である。このWH句の移動を制限する制約がある。その制約を一般にWHの島の制約と呼んでいる。島となるのは複合名詞句と文主語
と等位構造である（Ｗｅｂサイト：英語は - nifty）。
然るに、
（11）
③ 四［三〔二（一）〕］⇒
③［〔（一）二〕三］四。
④ 三（五［一四〔二）〕］⇒
④ （［一〔二）三〕四］五。
従って、
（10）（11）により、
（12）
③ You are doing what here? ⇒
③ あなたは、ここで何をしてゐる。
に付く「返り点」は、
③ 四　三　二　一
であって、
④ What are you doing here? ⇒
④ あなたは、ここで何をしてゐる。
に付く「返り点」は、
④ 三　五　一　四　二
であるものの、
④ 三　五　一　四　二
といった、「ユニークなそれ」は、「漢文訓読」では有り得ない。
然るに、
（13）
「漢文訓読」ではなく、「白話（中国語）訓読」であれば、（14）で示す通り、
⑤ 下　二　上　一
⑥ 二　五　三　一　四
⑦ 二　三レ　一
といふ、「ユニークなそれ」を、見ることが、出来る。
（14）

ｃｆ.
訓読法の限界は、白話文、つまり口語の文章には適用できないことだといわれます。つまり、文語（文言）の文章だけしか訓読法で読むことができないのです。中国語の文語文（つまり漢文）は、漢字の表意文字たる性質を十二分に生かして、簡潔な表現になっておりますから、訓に非常に適しています。これに対し、白話（口語）の文章は、熟語や助字が多く、冗長です。そのため訓読には不向きなのです（Ｗｅｂサイト：日本漢文の世界）。
従って、
（12）（13）（14）により、
（15）
④
What are you doing here? ⇒
④ あなたは、ここで何をしてゐる。
⑤ 只‐管要纏我 ⇒
⑤ ヒタスラ　我ガ　ヤツカイニナル。
⑥ 端‐的看不出這婆‐子的本‐事来 ⇒
⑥ 端的に這の婆子の本事を看出だし来たらず。
⑥ 西門慶促‐忙促－急儧‐造不出床来 ⇒
⑥ 西門慶促忙促急に床を儧造し出し来たらず。
⑦ 吃了不多酒 ⇒
⑦ 吃むこと多からず。
に付く「それは」は、
④ 三　五　一　四　二
⑤ 下　二　上　一
⑥ 二　五　三　一　四
⑦ 二　三レ　一
であるものの、
⑤ 下　二　上　一
⑦ 二　三レ　一
の場合は、このやうな「それ」が「返り点」でないことについての、「明言」が有る。
すなはち、
（16）
上中下点（上・下、上・中・下）
必ず一二点をまたいで返る場合に用いる（数学の式における（　）が一二点で、｛　｝が上中下点に相当するものと考えるとわかりやすい）。（原田種成、私の漢文講義、1995年、４１・４３頁）
とある以上、
⑤ 下　二　一　上
ではない、
⑤ 下　二　上　一
は、「返り点」ではない。
加へて、
（17）
三・四点も同じくレ点といっしょにはならない（江連隆、総合新漢文、1968年、１５頁）。
とある以上、
⑦ 三レ　
は、有り得ないため、
⑦ 二　三レ　一
は、「返り点」ではない。
（09）により、
（18）
④ 三　五　一　四　二
⑤ 下　二　上　一
⑥ 二　五　三　一　四
⑦ 二　三レ　一
といふ四つの内の、
④ 三　五　一　四　二
に対する「括弧」
④ （ ［ 〔　） 〕 ］
である。
（19）
⑤ 下　二　上　一
⑥ 二　五　三　一　四
⑦ 二　三レ　一
の場合、
⑤ 四　二　三　一
⑥ 二　五　三　一　四
⑦ 二　四　三　一
と「同じこと」であるが、
⑤ 四［二（三〔一）〕］
⑥ 二（五［三〔一）〕四］
⑦ 二（四［三〔一）〕］
である。
従って、
（18）（19）により、
（20）
④ （ ［ 〔　） 〕 ］
⑤ ［ （ 〔　） 〕 ］
⑥ （ ［ 〔　） 〕 ］
⑦ （ ［ 〔　） 〕 ］
であって、
④ 三　五　一　四　二
⑤ 四　二　三　一
⑥ 二　五　三　一　四
⑦ 二　四　三　一
であって、それ故、
④ ３＜５　１　４＞２
⑤ ４　２＜３＞１
⑥ ２＜５　３　１＞４
⑦ ２＜４　３＞１
であるものの、「結論」だけを、書くならば、
④ Ｌ＜Ｍ＞Ｎ　＆　Ｌ＝Ｎ＋１
といふ「語順」を含まない限り、「括弧」と「返り点」が、成立する。
従って、
（21）
④ ３＜５　１　４＞２
⑤ ４　２＜３＞１
⑥ ２＜５　３　１＞４
⑦ ２＜４　３＞１
といふ「順番」を、
④ ５＞３　１　２＜４
⑤ ４　３＞２＞１
⑥ ５＞３　２　１＜４
⑦ ４＞２　１＜３
といふ「順番」に換へれば、「括弧」と「返り点」は、成立する。
すなはち、
（22）
④ ５＞３　１　２＜４
⑤ ４　３＞２＞１
⑥ ５＞３　２　１＜４
⑦ ４＞２　１＜３
であれば、
④ ５〔３（１２）４〕
⑤ ４［３〔２（１）〕］
⑥ ５［３〔２（１）〕４］
⑦ ４〔２（１）３〕
であるため、
④ 〔 （　） 〕
⑤ ［ 〔 （　） 〕 ］
⑥ ［ 〔 （　） 〕 ］
⑦ 〔 （　） 〕
は、「括弧」であり、
④ ５＞３　１　２＜４
⑤ ４　３＞２＞１
⑥ ５＞３　２　１＜４
⑦ ４＞２　１＜３
といふ「順番」は、
④ 下　二　一　上
⑤ レ　レ　レ
⑥ 二　レ　レ　一
⑦ 二　レ　一
といふ「返り点」に、相当する。
ｃｆ.

平成２７年１０月０３日、毛利太。

返り点に対する「括弧（函）」の用法Ⅱｂ。

（01）
① 一　二　三　四　五　六　七　八　九　十　・ ・ ・ ・ ・
② 上　中　下
③ 甲　乙　丙　丁　戊　己　庚　辛　壬　癸
④ 天　地　人
⑤ レ
は、「返り点」である。
（02）
（03）～（21）に於いて、
① 二　三　一
② 下　二　上　一
③ 二　下　三　一　上
④ 三　二レ　一
といふ「順番」は、「返り点」ではない。といふことを、説明します。
（03）
① 不注意＝意を注がず。
の「返り点」は、
① レ　レ
である。
（04）
① 注不意＝意を注がず。
の「返り点」は、敢へて、さうするのであれば、
① 二　三　一
である。
ｃｆ.

然るに、
（05）
① 不注意＝意を注がず。
に対して、
① 注不意＝意を注がず。
といふ「漢文」は、有り得ないし、
① レ　レ
① 三　二　一
に対して、
① 二　三　一
といふ「返り点」は、見たことが無い。
（06）
一・二点をはさんで返る時は上・中・下点。上・中・下点をはさんで返る時は甲・乙点。甲・乙点をはさんで返る時は天・地（天・地・人）点である（志村和久、漢文早わかり、1982年、２０頁）。
然るに、
（07）
② 四　二　三　一
の場合は、
② 二　をはさんで、
② 三　から
② 四　へ返ってゐる。
従って、
（06）（07）により、
（08）
② 四　二　三　一
の場合は、
② 下　二　上　一
でなければ、ならない。
然るに、
（09）
② 下　二　上　一
であれば、
② 下　二　上　
であって、尚且つ。
② 二　上　一
である。
然るに、
（10）
② 下　二　上　
であれば、「上下点」が、「一二点」を挟んゐて、
② 二　上　一
であれば、「一二点」が、「上下点」を挟んゐる。
然るに、
（11）
一二点（一・二・三・・・・・・）二字以上を隔てて返る場合。
上中下点（上・下、上・中・下）
必ず一二点をまたいで返る場合に用いる（数学の式における（　）が一二点で、｛　｝が上中下点に相当するものと考えるとわかりやすい）。（原田種成、私の漢文講義、1995年、４１・４３頁）
従って、
（09）（10）（11）により、
（12）
② 下　二　上　一
といふ「それ」は、「返り点」ではない。
（13）
③ 二　五　三　一　四
の場合は、
③ 三　一　をはさんで、
③ 四　から
③ 五　へ返ってゐる。
従って、
（02）（13）により、
（14）
② 二　五　三　一　四
の場合は、
② 二　下　三　一　上
でなければ、ならない。
然るに、
（15）
② 二　下　三　一　上
であれば、
② 下　三　一　上
であって、尚且つ、
② 二　下　三　一
である。
然るに、
（16）
② 下　三　一　上
であれば、「上下点」が、「一二点」を挟んゐて、
② 二　下　三　一
であれば、「一二点」が、「上下点」を挟んゐる。
従って、
（11）（15）（16）により、
（17）
② 二　下　三　一　上
といふ「それ」は、「返り点」ではない。
（18）
③ 三　二レ　一
であれば、
③ 三　二　一　一
となって、
③ 一　一
となるため、
③ 二レ
といふ「返り点」は、有り得ない。
（19）
③ 四　三レ　二　一
であれば、
③ 四　三　二　二　一
となって、
③ 二　二
となるため、
③ 三レ
といふ「返り点」も、有り得ない。
従って、
（18）（19）により、
（20）
（1）一とレ点とはいっしょになって「一レ」となる。
（2）二とレ点とはいっしょになって「二レ」にはならない。
（3）三・四点も同じくレ点といっしょにならない。
（江連隆、総合 新漢文、1968年、１５頁改）
従って、
（20）により、
（21）
いづれにせよ、
③ 三レ
を含む、
③ 二　三レ　一
といふ「返り点」は、有り得ない。
従って、
（03）～（21）により、
（22）
① 二　三　一
② 下　二　上　一
③ 二　下　三　一　上
④ 三　二レ　一
といふ「順番」は、「返り点」ではない。
然るに、
（23）
その一方で、
② 只‐管要纏我 ⇒
② ヒタスラ　我ガ　ヤツカイニナル。
③ 端‐的看不出這婆‐子的本‐事来 ⇒
③ 端的に這の婆子の本事を看出だし来たらず。
③ 西門慶促‐忙促－急儧‐造不出床来 ⇒
③ 西門慶促忙促急に床を儧造し出し来たらず。
④ 吃了不多酒 ⇒
④ 吃むこと多からず。
といふ「白話文（中国語）」に於ける「順番」は、（24）で示す通り、
② 下　二　上　一
③ 二　五　三　一　四
③ 二　五　三　一　四
④ 二　三レ　一
である。
（24）

従って、
（22）（23）（24）により、
（25）
① 只‐管要纏我。
② 端‐的看不出這婆‐子的本‐事来。
② 西門慶促‐忙促－急儧‐造不出床来。
③ 吃了不多酒。
のやうな「中国語（白話文）」の場合は、「返り点」を加へることが、出来ない。
ｃｆ.
しかし私が専門にしている中国明清の白話小説は必ずしも漢文訓読の方法では読めません。「白話」というのは話し言葉をもとにした書面語で、それを読むためには現代中国語の知識が必要になります。皆さんがよく知っているでしょう『三国志演義』・『水滸伝』・『西遊記』・『封神演義』などはみな白話で書かれている長編小説です。これらの小説を読むためには、まず現代中国語をしっかり学ばなければなりません（Ｗｅｂサイト：中川諭|大東文化大学）。簡潔を旨として作られた文言文とは異なり、話し言葉に基づく白話文は、本来訓読には適していない（実際、現在では白話文の訓読はほとんど行われていない）。しかし江戸時代、白話文は訓読されていた（勉誠出版、続「訓読」論、2010年、３３０頁）。
従って、
（05）（23）（25）により、
（26）
① 二　三　一
② 下　二　上　一
③ 二　下　三　一　上
④ 二　三レ　一
すなはち、
① ２＜３＞１
② ４　２＜３＞１
③ ２＜５　３＞１　４
④ ２＜４　３＞１
といふ「順番」には、「返り点」を加へることが、出来ない。
然るに、
（27）
① ３＞２＞１
② ４　３＞２＞１
③ ５＞２　１＜３　４
④ ４＞２　１＜３
に対する「返り点」は、
① レ　レ
② レ　レ　レ
③ 二　レ　一
④ 二　レ　一
である。
従って、
（26）（27）により、
（28）
① ２＜３＞１
② ４　２＜３＞１
③ ２＜５　３＞１　４
④ ２＜４　３＞１
といふ「順番」には、「返り点」を加へることが、出来ないものの、
① ３＞２＞１
② ４　３＞２＞１
③ ５＞２　１＜３　４
④ ４＞２　１＜３
といふ「順番」には、「返り点」を加へることが、出来るであって、このことが、ここ迄の、「結論」である。
（29）
① 一　二　三　四　五　六　七　八　九　十　・ ・ ・ ・ ・
② 上　中　下
③ 甲　乙　丙　丁　戊　己　庚　辛　壬　癸
④ 天　地　人
⑤ レ
は、「返り点」であって、
① （　）
② 〔　〕
③ ［　］
④ ｛　｝
⑤ 〈　〉
は、「括弧」である。
（30）
（31）～（51）に於いて、
① ３＞２＞１
② ４　３＞２＞１
③ ５＞２　１＜３　４
④ ４＞２　１＜３
といふ「順番」には、「返り点」だけでなく、「括弧」を加へることが、出来るものの、
① ２＜３＞１
② ４　２＜３＞１
③ ２＜５　３＞１　４
④ ２＜４　３＞１
といふ「順番」には、「返り点」だけでなく、「括弧」を加へることが、出来ない。
といふことを、説明します。
（31）
① （　）は　　　 「小さな函」。
② 〔　〕は　　　「中位の函」。
③ ［　］は　　 　「大きな函」。
④ ｛　｝は　「より大きな函」。
⑤ 〈　〉は「もっと大きな函」。
に譬へることが、出来る。
（32）
①「小さな函」が、
②「中位の函」の中に、入ってゐる「状態」を、
② 〔 （　） 〕
とする。
（33）
②「中位の函」が、
①「小さな函」の中に、入ってゐる「状態」を、
① （ 〔　〕 ）
とする。
然るに、
（34）
②「Ｍサイズの箱」が、
①「Ｓサイズの箱」の中に、入ることは、物理的に、有り得ない。
従って、
（32）（33）（34）により、
（35）
① （ 〔　〕 ）
① （ 〔　） 〕
① 〔 （　〕 ）
といふ「函」は有り得ない。
但し、
（36）
② 〔（　）〕
だけでなく、
② 〔（　）（　）〕
② 〔（　）（　）（　）〕
であっても、
①「小さな箱」が、
②「中位の箱」の中に、入ることには、変はりがない。
従って、
（31）～（36）により、
（37）
① （　）
② 〔　〕
③ ［　］
④ ｛　｝
⑤ 〈　〉
に於いて、
② の中には、一つ以上の ① が有って、
③ の中には、一つ以上の ② が有って、
④ の中には、一つ以上の ③ が有って、
⑤ の中には、一つ以上の ④ が有る。
ならば、その時に限って、「括弧（函）」とする。
（38）
① ３＞２＞１
である時、
① ３〔２（１）〕
とする。
（39）
① ３〔２（１）〕。
に於いて、
① ２（　）⇒（１）２
① ３〔　〕⇒〔　〕３
とするならば、
① ３〔２（１）〕⇒
① 〔（１）２〕３。
といふ「並び替へ（ソート）」が、成立する。
然るに、
（40）
① ２＜３＞１
である時、
① ２（３〔１）〕
とする。
（41）
① ２（３〔１）〕
に於いて、
① ２（　）⇒（１）２
① ３〔　〕⇒〔　〕３
とするならば、
① ２（３〔１）〕⇒
① （〔１）２〕３。
といふ「並び替へ（ソート）」が、成立する。
然るに、
（35）により、
（42）
① 〔 （　） 〕
に対して、
① （ 〔　） 〕
は、「括弧」ではない。
従って、
（40）（41）（42）により、
（43）
① ３〔２（１）〕⇒
① 〔（１）２〕３。
といふ「並び替へ（ソート）」に於ける、
① 〔 （　） 〕
は、「括弧」であるが、
① ２（３〔１）〕⇒
① （〔１）２〕３。
といふ「並び替へ（ソート）」に於ける、
① （ 〔　） 〕
は、「括弧」ではない。
従って、
（38）～（43）により、
（44）
① ３＞２＞１
といふ「順番」に対しては、「括弧」を用ゐて行ふ、
① １＜２＜３
といふ「並び替へ（ソート）」が、可能である一方で、
① ２＜３＞１
といふ「順番」に対しては、「括弧」を用ゐて行ふ、
① １＜２＜３
といふ「並び替へ（ソート）」は、可能ではない。
従って、
（45）
２＜３＞１
のやうに、
Ｌ＜Ｍ＞Ｎ
に於いて、
Ｌ＝Ｎ＋１
であるならば、「それら順番」は、「返り点」では表すことが出来ず、尚且つ、「函（括弧）」に、入らない。
（46）
Ｌ＜Ｍ＞Ｎ　＆　Ｌ＝Ｎ＋１
といふことは、
Ｎ＜Ｌ＜Ｍ
といふ、ことである。
然るに、
（47）
Ｌ＜Ｍ＞Ｎ
を、
Ｎ＜Ｌ＜Ｍ
といふ「順番」に「並び替へる（ソートする）」ためには、
Ｌ（ＭＮ）
とした上で、
Ｌ（Ｍ〔Ｎ）〕
としなければならない。
然るに、
（48）
Ｌ（Ｍ〔Ｎ）〕
であれば、
（ 〔　） 〕
であるが、（29）により、
（ 〔　） 〕
は、「括弧」ではない。
然るに、
（49）
① ２＜３＞１
② ４　２＜３＞１
③ ２＜５　３＞１　４
④ ２＜４　３＞１
の場合は、全て、
Ｌ＜Ｍ＞Ｎ　＆　Ｌ＝Ｎ＋１
といふ「順番」を含んでゐて、尚且つ、（37）により、
① ２（３〔１）〕⇒
① （〔１）２〕３。
② ４［２（３〔１）〕］⇒
② ［（〔１）２〕３］４。
③ ２（５［３〔１）〕４］⇒
③ （［〔１）２〕３４］５。
④ ２（４［３〔１）〕］⇒
④ （［〔１）２〕３］４。
に於ける、
① （ 〔　） 〕
② ［ （ 〔　） 〕 ］
③ （ ［ 〔　） 〕 ］
④ （ ［ 〔　） 〕 ］
は、「括弧」ではない。
然るに、
（50）　　
① ３＞２＞１
② ４　３＞２＞１
③ ５＞２　１＜３　４
④ ４＞２　１＜３
の場合は、全て、
Ｌ＜Ｍ＞Ｎ　＆　Ｌ＝Ｎ＋１
といふ「順番」を含んでゐないし、尚且つ、（37）により、
① ３〔２（１）〕
② ４［３〔２（１）〕］
③ ５〔２（１）３４〕
④ ４〔２（１）３〕
に於ける、
① 〔 （　） 〕
② ［ 〔 （　） 〕 ］
③ 〔 （　） 〕
④ 〔 （　） 〕
は、「括弧」である。
従って、
（26）（27）（49）（50）により、
（51）
① ３＞２＞１
② ４　３＞２＞１
③ ５＞２　１＜３　４
④ ４＞２　１＜３
といふ「順番」には、「返り点」だけでなく、「括弧」を加へることが、出来るものの、
① ２＜３＞１
② ４　２＜３＞１
③ ２＜５　３＞１　４
④ ２＜４　３＞１
といふ「順番」には、「返り点」だけでなく、「括弧」を加へることが、出来ないのであって、このことが、ここ迄の、「結論」である。
（37）により、
（52）
① 〈｛［〔（　）〕（　）］｝〉
は、「括弧（箱）」である。
然るに、
（53）
① １Ｆ〈２Ｅ｛３Ｄ［９〔７（４５６）８〕Ｃ（ＡＢ）］｝〉。
に於いて、
Ｆ〈　〉⇒〈　〉Ｆ
Ｅ｛　｝⇒｛　｝Ｅ
Ｄ［　］⇒［　］Ｄ
９〔　〕⇒〔　〕９
７（　）⇒（　）７
Ｃ（　）⇒（　）Ｃ
とするならば、
① １〈２｛３［〔（４５６）７８〕９（ＡＢ）Ｃ］Ｄ｝Ｅ〉Ｆ。
従って、
（52）（53）により、
（54）
① １＜Ｆ＞２＜Ｅ＞３＜Ｄ＞９＞７＞４＜５＜６＜８＜Ｃ＞Ａ＜Ｂ
といふ「１６進数」は、
① 〈｛［〔（　）〕（　）］｝〉
といふ「括弧」を介して、
① １＜２＜３＜４＜５＜６＜７＜８＜９＜Ａ＜Ｂ＜Ｃ＜Ｄ＜Ｅ＜Ｆ
といふ「昇べき順」に、「並び替へること（ソート）」が、可能である。
従って、
（54）により、
（55）
１＝我
Ｆ＝不
２＝必
Ｅ＝使
３＝人
Ｄ＝求
９＝以
７＝解
４＝中
５＝国
６＝語
８＝法
Ｃ＝解
Ａ＝漢
Ｂ＝文
であるならば、
① 〈｛［〔（　）〕（　）］｝〉
といふ「括弧」を介して、
① 我不必使人求以解中国語法解漢文＝
① 我不〈必使｛人求［以〔解（中国語）法〕解（漢文）］｝〉＝
① １Ｆ〈２Ｅ｛３Ｄ［９〔７（４５６）８〕Ｃ（ＡＢ）］｝〉⇒
① １〈２｛３［〔（４５６）７８〕９（ＡＢ）Ｃ］Ｄ｝Ｅ〉Ｆ＝
① 我〈必｛人［〔（中国語）解法〕以（漢文）解］求｝使〉不＝
① 我〈必ずしも｛人をして［〔（中国語を）解する法を〕以て（漢文を）解せんことを］求め｝使め〉不＝
① 私は必ずしも、人に対して、中国語を理解する方法を用ゐて、漢文を理解することを、求めさせない。
といふ「漢文訓読」が、成立する。
（56）
① 我不必使人求以解中国語法解漢文
から、「返り点」が付かない「それ」を除くと、
Ｆ＝不
Ｅ＝使
Ｄ＝求
９＝以
７＝解
６＝語
８＝法
Ｃ＝解
Ｂ＝文
然るに、
（57）
Ｆ＝不 ⇒ 九＝不
Ｅ＝使 ⇒ 八＝使
Ｄ＝求 ⇒ 七＝求
９＝以 ⇒ 四＝以
７＝解 ⇒ 二＝解
６＝語 ⇒ 一＝語
８＝法 ⇒ 三＝法
Ｃ＝解 ⇒ 六＝解
Ｂ＝文 ⇒ 五＝文
従って、
（06）（57）により、
（58）
九＝不 ⇒ 戊＝不
八＝使 ⇒ 丁＝使
七＝求 ⇒ 丙＝求
四＝以 ⇒ 下＝以
二＝解 ⇒ 二＝解
一＝語 ⇒ 一＝語
三＝法 ⇒ 上＝法
六＝解 ⇒ 乙＝解
五＝文 ⇒ 甲＝文
従って、
（58）により、
（59）
② 不使求以解語法解文＝
② 不〈使｛求［以〔解（語）法〕解（文）］｝〉＝
② 戊〈丁｛丙［下〔二（一）上〕乙（甲）］｝〉⇒
② 〈｛［〔（一）二上下〕（甲）乙］丙｝丁〉戊＝
② 〈｛［〔（語）解法〕以（文）解］求｝使〉不＝
② 〈｛［〔（語を）解する法を〕以て（文を）解せんことを］求め｝使め〉不。
従って、
（54）～（59）により、
（60）
① 我不必使人求以解中国語法解漢文。
② 不使求以解語法解文。
が入る「括弧（箱）」は、
① 〈｛［〔（　）〕（　）］｝〉
② 〈｛［〔（　）〕（　）］｝〉
であって、「返り点」は、
① 戊　丁　丙　下　二　一　上　乙　甲
② 戊　丁　丙　下　二　一　上　乙　甲
である。
然るに、
（61）

従って、
（60）（61）により、
（62）
① 我不必使人求以解中国語法解漢文。
② 不使求以解語法解文。
に付く「返り点」は、両方とも、
① 戊　丁　丙　下　二　一　上　乙　甲
② 戊　丁　丙　下　二　一　上　乙　甲
であるものの、
② 不使求以解語法解文。
の場合は、「レ点」を用ゐる。といふ「規則」により、
② レ　レ　下　二　レ　一　上レ　
としなければ、ならない。
（63）
③ 恐衆狙之不馴於己＝
③ 恐［衆狙之不〔馴（於己）〕］⇒
③［衆狙之〔（於己）馴〕不］ 恐＝
③［衆狙の〔（己に）馴れ〕不るを］ 恐る。
の「返り点」は、
③ 四　三　　二　一
③ 二　一レ　二　一
の内の、
③ 二　一レ　二　一
である。
（64）
④ 非不読書＝
④ 非［不〔読（書）〕］⇒
④ ［〔（書）読〕不］非＝
④ ［〔（書を）読ま〕不る］非ず。
の「返り点」は、
④ 四　三　二　一
ではなく、
④ レ　レ　レ
である。
ｃｆ.
映像： 非不読書
然るに、
（65）
② レ　レ　下　二　レ　一　上レ　
③ 二　一レ　二　一
④ レ　レ　レ
は、「レ点の使い方」の全てを、網羅する。
従って、
（01）～（65）により、
（66）
① （　）
② 〔　〕
③ ［　］
④ ｛　｝
⑤ 〈　〉
といふ「括弧」は、「括弧の種類」が、「不足」しない限り、
① 一　二　三　四　五　六　七　八　九　十　・ ・ ・ ・ ・
② 上　中　下
③ 甲　乙　丙　丁　戊　己　庚　辛　壬　癸
④ 天　地　人
⑤ レ
といふ「返り点」の「役割」を担ひ、
① 一　二　三　四　五　六　七　八　九　十　・ ・ ・ ・ ・
② 上　中　下
③ 甲　乙　丙　丁　戊　己　庚　辛　壬　癸
④ 天　地　人
⑤ レ
は、「上　中　下」や「天　地　人」で、「不足」が生じない限り。
① （　）
② 〔　〕
③ ［　］
④ ｛　｝
⑤ 〈　〉
といふ「括弧」の「役割」を、担ふことになる。
（67）
「支那の言語や文字を研究するのに、漢文と支那語の様な区別を設けてゐるのは、世界中、日本だけで、支那はもとより、ヨーロッパやアメリカで支那学を研究するにも、そんな意味のない
区別など夢にも考へてゐない。西洋人が支那のことを研究するには、何よりも先き、支那の現代の言葉を学び、現代人の書く文章を読み、それから次第に順序を追うて、古い言葉で書いた書物を読んで、支那民族の文化の深淵を理解する。アメリカの大学で支那のことを研究する学生は、最初の年に現代語学現代文学を学び、次の年に歴史の書物を読み経書を習ふさうである（勉誠出版、「訓読」論、2008年、５７頁）。
然るに、
（68）
① 〈｛［〔（　）〕（　）］｝〉
といふ「括弧」を介して、
① 我〈必ずしも｛人をして［〔（中国語を）解する法を〕以て（漢文を）解せんことを］求め｝使め〉不＝
① 我〈必｛人［〔（中国語）解法〕以（漢文）解］求｝使〉不⇒
① 我不〈必使｛人求［以〔解（中国語）法〕解（漢文）］｝〉＝
① 我不必使人求以解中国語法解漢文。
といふ「漢作文」が、可能であるといふことは、「漢文」と「訓読」に於いて、
Ａ：「語順」は異なるが、
Ｂ：「括弧（シンタックス）」は等しい。
といふことを、意味してゐる。
従って、
（69）
既に確認したやうに、「中国語（白話）」に対して、しばしば、「返り点・括弧」が付けられないのであれば、その場合は、「和文」と「中国語（白文）」に於いて、
Ａ：「語順」だけでなく、
Ｂ：「括弧（シンタックス）」も等しくない。
といふことを、意味してゐる。
加へて、
（70）
日本人が漢文を書く場合、漢文直訳体の日本語である漢文訓読は、有力な道具となり得る。まず頭のなかで漢文訓読体の日本語を思ひ浮かべ、それを漢文の語序にしたがって書く。次に、そうして書きあがった漢文を自分で訓読し、定型的な「句法」訓読できない箇所はないか、返り点に無理はないか、などをチェックする。実際に漢詩・漢文を自分で書いてみればわかることだが、日本人が音読直読だけで純正漢文を書くことは、なかなかに難しい（そもそも漢文の音読直読ができる現代中国人でも、純正漢文が書ける者は少ない）。
（勉誠出版、「訓読」論、2008年、２６５頁）
（71）
今の日本の中学・高校では英語・数学・国語を主要３教科と呼んでいますが、戦前、旧制の中学では英語・数学・国語・漢文が主要４教科でした。漢文は国語とは独立した教科だったんですね。読解はもとより、復文（書き下し文から原文を復元）や作文もやるし、これだけ高度な学習内容でしたから、白文の読解もなんのそのでした。しかし戦後、漢文は国語の一部である古典分野の、そのまた片隅に追いやられてしまいました。漢文の得意な教師は少なく、漢文に興味を持つ生徒も少なく、おまけに最近は大学入試科目から漢文が消えつつあるので、みんないやいやながら学んでいます。内容もたいしたことはなく、学者先生が返り点と送り仮名をつけた文章をえっちらおっちら読む程度です（Ｗｅｂサイト：漢文入門）。
従って、
（67）～（71）により、
（72）
ヨーロッパ人やアメリカ人にとってはともかく、日本人にとって、「音読直読」が、「漢文訓読」よりも、殊更に優れた「方法」であるとは、思へない。
（73）
仮に、「劣った方法」であらうとなからうと、アイヌ語や、ゲール語や、ピダハン語が、「消滅」してはならないのであれば、たとへ、「話し言葉」ではなくとも、明らかに、ユニークな「漢文訓読」は、「消滅」すべきではない。
平成２７年１０月０１日、毛利太。