「昨日の記事」を書き換へます。―
（01）
食（馬）＝（馬を）食べる。
ではなく、
食（馬）＝（馬を）養ふ。
である。
従って、
（01）により、
（02）
（イ）食（馬）者不〔知（其能千里）而食〕也。
（ロ）食（馬）者不〔知（其能千里）〕而食也。
ではなく、
（イ）養（馬）者不〔知（其能千里）而養〕也。
（ロ）養（馬）者不〔知（其能千里）〕而養也。
とする。
従って、
（03）
（イ）養（馬）者
（ロ）養（馬）者
を除くと、
（イ）不〔知（其能千里）而養〕也。
（ロ）不〔知（其能千里）〕而養也。
である。
然るに、
（04）
＊新注では、「祝鮀の佞ありて宋朝の美あらずんば、」と読み、佞美の両方がなければと解する（金谷治、論語、1963年、１１６頁）。
もっとも以上は、朱子の注の読み方であり、古注では、「祝鮀の佞有らずして宋朝の美有るは、今の世に免れ難し」、つまり弁舌はなくて、美貌だけもっているものは、あぶない（吉川幸次郎、論語上、1965年、１６７頁）。
とあるやうに、「論語、雍也第六、一六」は、
（イ）不〔有（祝鮀之佞）而有（宋朝美）〕。
（ロ）不〔有（祝鮀之佞〕而有（宋朝美）。
といふ、「二通りの解釈」が、可能である。
従って、
（03）（04）により、
（05）
（イ）不 知其能千里 而 養也（雑説、韓愈）。
（イ）不 有祝鮀之佞 而 有宋朝美（論語、雍也）。
は、それぞれ、「二通りの解釈」が、可能である。
然るに、
（06）
（イ）其の能の千里なるを知りて養は不るなり（雑説、韓愈）。
といふ「訓読」であっても、
（イ）〔（其の能の千里なるを）知りて養は〕不るなり。
（ロ）（其の能の千里なるを）知りて（養は）不るなり。
といふ、「二通りの解釈」が、可能である。
従って、
（05）（06）により、
（07）
（イ）不知其能千里而養也（雑説、韓愈）。
（イ）其の能の千里なるを知りて養は不るなり（雑説、韓愈）。
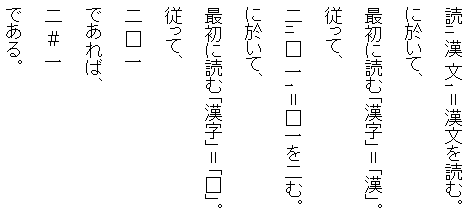
といふ「漢文訓読」は、「二通りの解釈」が、可能であって、（08）に示す画像は、そのことを、述べてゐる。
（08）
然るに、
（09）
（イ）不〔知（其能千里）而養〕也。
（ロ）不〔知（其能千里）〕而養也。
であれば、中西清先生が指摘してゐる通り、「返り点」は、
（イ）下 二 一 上
（ロ）レ 二 一
であって、尚且つ、
（イ）不〔知（其能千里）而養〕也。
（ロ）不〔知（其能千里）〕而養也。
の「意味」は、同じではない。
然るに、
（10）
「結論」として、
（イ）養（馬）者不〔知（其能千里）而養〕也。
（ロ）養（馬）者不〔知（其能千里）〕而養也。
であれば、「返り点」は、
（イ）下 二 一 上
（ロ）レ 二 一
であって、尚且つ、「論理的」には、「どちらでも良い」。
すなはち、
（11）
（イ）養馬者不知其能千里而養也＝
（イ）養（馬）者不〔知（其能千里）而養〕也⇒
（イ）（馬）養者〔（其能千里）知而養〕不也＝
（イ）（馬を）養ふ者は〔（其の能の千里なるを）知りて養は〕不るなり。
に対する、
（ロ）養馬者不知其能千里而養也＝
（ロ）養（馬）者不〔知（其能千里）〕而養也⇒
（ロ）（馬）養者〔（其能千里）知〕不而養不也＝
（ロ）（馬を）養ふ者は〔（其の能の千里なるを）知ら〕不して養ふなり。
であれば、「論理的」に、「変はりが無い」。
（12）
～＝不
Ｐ＝知其能千里＝その馬に千里の能力があることを知る。
＆＝而＝そして、
Ｑ＝養馬＝その馬を養ふ。
とする。
従って、
（12）により、
（13）
（イ）不〔知（其能千里）而養〕也＝
（イ）其の能の千里なるを知りて養はざるなり。
の場合は、
（イ）～（Ｐ＆Ｑ）
であって、
（ロ）不〔知（其能千里）〕而食也＝
（ロ）其の能の千里なるを知らずして養ふなり。
の場合は、
（ロ）～（Ｐ）＆Ｑ
である。
従って、
（13）により、
（14）
つまり（ロ）は、知らないけれども養うことは養っていることになるが、（イ）の方は「知りかつ養う」ことを否定しているので、養っているかどうかもわからないことになる（中西清、漢文研究、1956年、２９２頁）。
然るに、
（15）
（イ）養（馬）者不〔知（其能千里）而養〕也＝
（イ）馬を養ふ者は、其の能の千里なるを知りて養はざるなり。
の場合は、
（イ）Ｑ，～（Ｐ＆Ｑ）
であって、
（ロ）養（馬）者不〔知（其能千里）〕而食也＝
（ロ）馬を養ふ者は、其の能の千里なるを知らずして養ふなり。
の場合は、
（ロ）Ｑ，～（Ｐ）＆Ｑ
である。
然るに、
（16）
「ド・モルガンの法則、交換則、含意の定義、二重否定」により、
（イ）Ｑ，～（Ｐ＆Ｑ）＝
（イ）Ｑ，～（Ｐ）∨～（Ｑ）＝
（イ）Ｑ，～（Ｑ）∨～（Ｐ）＝
（イ）Ｑ，～（～（Ｑ））→～（Ｐ）＝
（イ）Ｑ，Ｑ→～（Ｐ）
然るに、
（17）
「前件肯定」により、
（イ）Ｑ，Ｑ，～（Ｐ）
（18）
「連言導入」により、
（イ）Ｑ，Ｑ＆～（Ｐ）
（19）
「交換則」により、
（20）
（イ）Ｑ，～（Ｐ）＆Ｑ
従って、
（16）（20）により、
（21）
（イ）Ｑ，～（Ｐ＆Ｑ）＝
（イ）Ｑ，Ｑ→～（Ｐ）∴
（イ）Ｑ，～（Ｐ）＆Ｑ
従って、
（13）（21）により、
（22）
（イ）Ｑ，～（Ｐ＆Ｑ）∴
（ロ）Ｑ，～（Ｐ）＆Ｑ
従って、
（15）（22）により、
（23）
（イ）養（馬）者不〔知（其能千里）而養〕也。であるならば、
（ロ）養（馬）者不〔知（其能千里）〕而養也。である。
従って、
（15）（23）により、
（24）
（イ）馬を養ふ者は、其の能の千里なるを知りて養はざるなり。であるならば、
（ロ）馬を養ふ者は、其の能の千里なるを知らずして養ふなり。である。
従って、
（21）（24）により、
（25）
（イ）「馬を養ふ者は、其の能の千里なるを知りて養はざるなり。」と言ふ一方で、
（イ）「馬を養ふ者が、其の能の千里なるを知ってゐる。」とすれば、「矛盾」するため、
（イ）「馬を養ふ者は、其の能の千里なるを知りて養はざるなり。」と言ふのであれば、
（ロ）「馬を養ふ者は、其の能の千里なるを知らずして養ふなり。」とせざるを得ない。
が故に、
（イ）「馬を養ふ者は、其の能の千里なるを知りて養はざるなり。」と言ふのであれば、
（ロ）「馬を養ふ者は、其の能の千里なるを知らずして養ふなり。」と言ふことになる。
ものの、このことは、「命題論理」で言へば、
（イ）Ｑ，～（Ｐ＆Ｑ）＝
（イ）Ｑ，Ｑ→～（Ｐ）∴
（イ）Ｑ，～（Ｐ）＆Ｑ
といふことに、他ならない。
従って、
（23）（24）（25）により、
（26）
（イ）養（馬）者不〔知（其能千里）而養〕也。であるならば、
（ロ）養（馬）者不〔知（其能千里）〕而養也。である。
といふ「命題」は、「論理的」にも、「正しい」。
従って、
（08）（26）により、
（27）
（イ）食馬者不知其能千里而養也。
の「返り点」は、
（イ）下 二 一 上
であっても、
（ロ）レ 二 一
であっても、どちらでも、「間違ひ」ではない。
然るに、
（28）
（イ）「その馬の能力が千里であることを知った上で養ってゐる。のではない。」といふ場合は、
（イ）「その馬の能力が千里であることを知らない。」といふことを、「間接的に、述べてゐる」。
（29）
（ロ）「その馬の能力が千里であることを知らずに、養ってゐる。」といふ場合は、
（ロ）「その馬の能力が千里であることを知らない。」といふことを、「直接的に、述べてゐる」。
然るに、
（30）
（研究）この文は明君を伯楽に、賢臣を千里の馬にたとえたものである。全文比喩を用いてあるが、比喩ではなくこれを明君と賢臣に置きかえたらどういうことになるであろうか。文章の味もないし、これを読んだ君を怒らして厳罰を受けるであろう。すぐれた人物がいても、これを見出して用いる明君がいない。だから人材は空しく民間に埋もれたまま死んでいく。― 中略 ―、以上のような趣旨で、明君賢臣の関係を論じたものである。
（中西清、漢文研究、1956年、２９１頁）
従って、
（28）（29）（30）により、
（31）
（ロ）あなたは、明君でないので、私のような賢臣がゐても、あなたは、私の真価に、気づかない。
といふ風に、ストレートには、言ひにくい。はずである。
従って、
（31）により、
（32）
（ロ）不知其能千里而養也＝
（ロ）不〔知（其能千里）〕而養也＝
（ロ）〔（其の能の千里なるを）知ら〕不して養ふなり＝
（ロ）その馬の能力が千里であることを知らずに、養ってゐる。
であるより、
（イ）不知其能千里而養也＝
（イ） 不〔知（其能千里）而養〕也＝
（イ）〔（其の能の千里なるを）知りて養は〕不るなり＝
（イ）その馬の能力が千里であることを知った上で養ってゐる。のではない。
であるものと、思はれる。
従って、
（32）により、
（33）
（イ）不知其能千里而養也。
の「返り点・括弧」は、
（イ）下 二 一 上
（イ）〔 （ ） 〕
である。
然るに、
（12）～（26）により、
（34）
（イ）養（馬）者不〔知（其能千里）而養〕也。であるならば、
（ロ）養（馬）者不〔知（其能千里）〕而養也。である。
といふ「命題」は、「論理的」にも、「正しい」ことが、
（イ）Ｑ，～（Ｐ＆Ｑ）＝
（イ）Ｑ，Ｑ→～（Ｐ）∴
（ロ）Ｑ，～（Ｐ）＆Ｑ
といふことに、他ならない。にも、拘はらず、
（イ）養馬者不（知其能千里而養）也。であるならば、
（ロ）養馬者不（知其能千里）而養也。である。
ではない。としたら、「漢文」と「命題論理」は、「矛盾」する。
従って、
（35）
「漢文」と「命題論理」は、「矛盾」しないのであれば、
（イ）養馬者不（知其能千里而養）也。であるならば、
（ロ）養馬者不（知其能千里）而養也。である
といふことは、「漢文」自体で考へても「正しい」。と、せざるを得ない。
従って、
（35）により、
（36）
少なくとも、
（イ）養馬者不知其能千里而養也。
といふ『雑説、韓愈』に、「括弧」は、有ります。
平成２７年１２月２８日、毛利太。
― 「１２月２３日の記事」を書き換へます。―
（01）
漢語においては、その実詞に属する単語は、上述のように、介詞や接続詞など、その文法的関係を示すものをなにも用いずに、孤立的に配置されていることが多い。しかし、その配列されている単語の間の文法的な関係によって、その配列のしかたに、一定の順序がある。それで、漢語は、この単語の配列のしかたが、その文法の重要な基礎となっているわけである。この漢語文法の基礎となっている文法的な関係として、次の四つの関係をあげることができる。
（一）主述関係 主語 ― 述語
（二）修飾関係 修飾語 ― 被修飾語
（三）補足関係 叙述語 ― 補足関係
（四）並列関係 並列語 ― 並列語
（鈴木直治、中国語と漢文、1975年、２８１～２８３頁改）
（02）
（二）修飾関係 修飾語 ― 被修飾語 は、
（ａ）連用修飾 と、
（ｂ）連体修飾 に、分けることが出来、
（ａ）は、おおむね、「副詞」であって、
（ｂ）は、おおむね、「形容詞」である。
従って、
（01）（02）により、
（03）
例へば、
（ａ）常読＝常＋読
（ｂ）漢文＝漢＋文
であれば、
（ａ）常 と、
（ｂ）漢 は、「（二）修飾語」である。
然るに、
（04）
① 不常読漢文＝
② 不｛常読（漢文）｝⇒
③ ｛常（漢文）読｝不＝
③ ｛常には（漢文を）読ま｝ず。
といふ「漢文訓読」は、「正しい」。
従って、
（04）により、
（05）
② 不｛ ｝⇒｛ ｝不
② 読（ ）⇒（ ）読
といふ「倒置」は、「正しい」。
然るに、
（06）
漢語における語順は、国語と大きく違っているところがある。すなわち、その補足構造における語順は、国語とは全く反対である。
（鈴木直治、中国語と漢文、1975年、２９６頁）
従って、
（01）（05）（06）により、
（07）
① 不常読漢文＝
② 不｛常読（漢文）｝。
に於ける、
② 不｛ ｝
② 読（ ）
といふ「二つ」は、「（三）補足関係」を、表してゐる。
従って、
（03）（07）により、
（08）
① 不常読漢文＝
② 不｛常＋読（漢＋文）｝。
とすれば、
② 不｛常＋読（漢＋文）｝。
といふ「形」は、
① 不常読漢文。
といふ「漢文」の、
（三）補足関係 叙述語 ― 補足関係
（二）修飾関係 修飾語 ― 被修飾語
を、表してゐる。
然るに、
（09）
② Ｅ｛Ａ＋Ｄ（Ｂ＋Ｃ）｝
は、「数式」である。
従って、
（09）により、
（10）
② 不｛常＋読（漢＋文）｝
であっても、「数式」であると、することが、可能である。
従って、
（08）（10）により、
（11）
② 不｛常＋読（漢＋文）｝
は、「漢文」であるとすれば「漢文」であって、「数式」であるとすれば、「数式」である。
然るに、
（10）
② 分配法則 により、
② Ｅ｛Ａ＋Ｄ（Ｂ＋Ｃ）｝＝
② Ｅ｛Ａ＋（ＤＢ＋ＤＣ）｝＝
② ｛ＥＡ＋Ｅ（ＤＢ＋ＤＣ）｝＝
② ｛ＥＡ＋（ＥＤＢ＋ＥＤＣ）｝
である。
従って、
（10）により、
（11）
② Ｅ｛Ａ＋Ｄ（Ｂ＋Ｃ）｝
といふ「数式」に於いて、
② Ｄ は、
②（Ｂ＋Ｃ） に、「係ってゐて」、
② Ｅ は、
② ｛Ａ＋Ｄ（Ｂ＋Ｃ）｝ に、「係ってゐる」。
然るに、
（12）
② 不｛常＋読（漢＋文）｝
といふ「漢文」に於いて、
② （漢文を）読む。
であるため、
② 読 は、
② （漢＋文） に、「係ってゐる」。
（13）
② 不｛常＋読（漢＋文）｝
の場合は、
②「常に漢文を読む。」といふワケではない。
といふ「意味」である。
従って、
（13）により、
（14）
② 不｛常＋読（漢＋文）｝
に於いて、
② 不 は、
② ｛常＋読（漢＋文）｝ に、「係ってゐる」。
従って、
（11）（12）（14）により、
（15）
「数式」と見なしても、
「漢文」と見なしても、
② 不｛常＋読（漢＋文）｝
に於いて、
② 読 は、
② （漢＋文） に、「係ってゐて」、
② 不 は、
② ｛常＋読（漢＋文）｝ に、「係ってゐる」。
然るに、
（16）
然るに、
（ ），｛ ｝
【読み】 かっこ、ちゅう（中）かっこ
【意味】 括弧の中を先に計算する。計算の順序を指示する用途で使う。
（瀬山士郎、数学記号を読む辞典、2013年、５３頁）
従って、
（16）により、
（17）
（ ）の中を先に計算する。
｛ ｝の中を先に計算する。
従って、
（17）により、
（18）
② ５×｛１＋４×（２＋３）｝
といふ「計算の順序」は、
③ ｛１＋（２＋３）×４｝×５＝
③ ｛１＋（５）×４｝×５＝
③ ｛１＋２０｝×５＝
③ ｛２１｝×５＝
③ １０５
といふ「順序」で、行はれる。
然るに、
（19）
② 不｛常読（漢文）｝⇒
③ ｛常（漢文）読｝不＝
③ ｛常には（漢文を）読ま｝ず。
であるため、
② 不×｛常＋読×（漢＋文）｝＝
② ｛常＋（漢＋文）×読｝×不
である。
従って、
（18）（19）により、
（20）
② ５×｛１＋４×（２＋３）｝＝
③ ｛１＋（２＋３）×４｝×５
であって、
② 不×｛常＋読×（漢＋文）｝＝
② ｛常＋（漢＋文）×読｝×不
である。
従って、
（15）（20）により、
（21）
① 不常読漢文＝
② 不｛常＋読（漢＋文）｝＝
② ｛常＋（漢＋文）×読｝×不。
といふ「漢文」は、敢へて、さうしたいのであれば、「数式」であると、見なすことが、出来る。
従って、
（01）～（21）により、
（22）
あたかも、
① ５×１＋４×２＋３＝１６
ではなく、
① ５×１＋４×２＋３＝１０５
であるならば、
① ５×１＋４×２＋３＝１０５＝
② ５×｛１＋４×（２＋３）｝＝１０５
であるやうに、
① 不常読漢文＝常には漢文を読まず。
である以上、
① 不常読漢文＝
② 不｛常＋読（漢＋文）｝。
であると、すべきである。
従って、
（23）
例へば、
① 不常読漢文。
といふ「漢文」は、
① 不常読漢文＝フツジョウトクカンブン。
といふ風に、読まうと、
① 不常読漢文＝常には漢文を読まず。
といふ風に、読まうと、固より、
② 不｛常＋読（漢＋文）｝。
といふ、
②「補足構造 叙述語 ― 補足関係」
②「修飾構造 修飾語 ― 被修飾語」
をしてゐる。
従って、
（24）
論語でも孟子でも、訓読をしないと気分が出ないといふ人もあるが、これは孔子や孟子に日本人になってもらはないと気が済まないのと同様で、漢籍が国書であり、漢文が国語であった時代の遺風である。支那の書物が、好い国語に翻訳されることは、もっとも望ましいことであるが、翻訳された結果は、多かれ少なかれその書物の持ち味を棄てることは免れない、立体的なものが平面化することが想像される。持ち味を棄て、平面化したものに慣れると、その方が好くなるのは、恐るべき麻痺であって、いはば信州に育ったものが、生きのよい魚よりも、塩鮭をうまいと思ふ様ものである（勉誠出版、訓読論、2008年、６０頁）。両者の亀裂は、戦後も親中国革新派の音読、反中国保守派の訓読として、ある意味で現在にまでつづいている（金文京、漢文と東アジア、2010年、８８・９頁）。
といふことで、あらふと、であるまいと、「括弧」は、有ります！
平成２７年１２月２４日、毛利太。
― 「一昨日の記事」を書き直します。―
（01）
６：（３／２）＝４：１ ⇔
６÷（３／２）＝４ ⇔
６＝（３／２）×４ ⇔
６は（３／２）の４倍である。
従って、
（01）により、
（02）
６：（３／２）＝囗：１
６÷（３／２）＝囗
６＝（３／２）×囗
といふ「問題」は、三つとも、
（３／２）を「何倍」すると、６になるか。
といふ「問題」に、等しい。
然るに、
（03）
｛（３／２）×（２／３）＝１｝×６＝６
従って、
（04）
（３／２）×｛（２／３）×６｝＝６
（３／２）×｛６×（２／３）｝＝６
（04）により、
（05）
（３／２）を｛６×（２／３）｝倍すると、６になる。
従って、
（02）（05）により、
（06）
６÷（３／２）＝囗
といふ「問題」は、
（３／２）を「何倍」すると、６になるか。
といふ「問題」に、等しく、尚且つ、
（３／２）×｛６×（２／３）｝＝６ ⇔
（３／２）を｛６×（２／３）｝倍すると、６になる。
従って、
（06）により、
（07）
６÷（３／２）＝６×（２／３）
従って、
（07）により、
（08）
囗÷（３／２）＝囗×（２／３）
従って、
（01）～（08）より、
（09）
「分数の割り算の答へ」は、「分母と分子を逆」にした「掛け算の答へ」に等しい。
（10）
６０＝１５＋１５＋１５＋１５
ならば、
６０は１５の４倍である。
（11）
６０が１５の４倍である。
ならば、
６．０は１．５の４倍である。
然るに、
（12）
６．０＝６
１．５＝３／２
従って、
（10）（11）（12）により、
（13）
６．０が１．５の４倍である。
ならば、
６は（３／２）の４倍である。
然るに、
（14）
６が（３／２）の４倍である。
ならば、
６＝（３／２）×４
（15）
６＝（３／２）×４
ならば、
６：（３／２）＝４：１
（16）
６：（３／２）＝４：１
ならば、
６÷（３／２）＝４
従って、
（10）～（16）により、
（17）
６：（３／２）＝４：１
６÷（３／２）＝４
６＝（３／２）×４
従って、
（18）
６：（３／２）＝囗：１
６÷（３／２）＝囗
６＝（３／２）×囗
といふ「問題」は、三つとも、
（３／２）を「何倍」すると、６になるか。
といふ「問題」に、等しい。
然るに、
（19）
「Ａ＝Ｂ×Ｃ」の「読み方」は、
「ＡイコールＢかけるＣ。」である。
然るに、
（20）
「イコール」＝「に等しい」、「×」＝「倍」。
従って、
（19）（20）により、
（21）
「Ａ＝Ｂ×Ｃ」
といふ「数式」を、
「ＡイコールＢかけるＣ。」
と読むことは、
「Ａに等しいＢ倍Ｃ。」
と読むことに、等しい。
然るに、
（22）
Ａ＝Ｂ×Ｃ
Ａ＝〔Ｂ×（Ｃ）〕
Ａ〔Ｂ（Ｃ）×〕＝
Ａは〔Ｂの（Ｃ）倍〕に等しい。
従って、
（23）
「Ａ＝Ｂ×Ｃ」といふ「数式」を、
「ＡはＢのＣ倍に等しい。」といふ風に、理解するためには、
「返り点・括弧」を、必要とする。
ｃｆ.
従って、
（24）
「日本語」であれば、
Ａ Ｂ Ｃ × ＝
と書くべきところが、
「数学語」では、
Ａ ＝ Ｂ × Ｃ
といふ「順番」で書かれてゐる。
（25）
数学を和文で表現するときに、最初にトラブルに陥るのが、否定をどのように表現するか、という問題です、次の和文を読んでみてください。
ＡならばＢでない。
この文は、２つの解釈があります。ひとつは「（ＡならばＢ）でない」。数文であらわすと、￢（Ａ→Ｂ）です。もうひとつは「Ａならば（Ｂでない）」。数文であらわすと、 Ａ→￢Ａ となります。この２つは全く異なる意味をもちますが、和文であらわそうとすると、どちらも同じ文になってしまうのです。
（新井紀子、数学は言葉、2009年、１２３頁）
然るに、
（26）
「ＡならばＢでない。」であれば、Ａ→Ｂ￢ と、書くべきであり、
「ＡならばＢである。ではない。」であれば、（Ａ→Ｂ）￢ と、書くべきである。
従って、
（24）（26）により、
（27）
「数学」にせよ、「論理学」にせよ、「日本語の語順」とそれらの「語順」は、同じではなく、この点は、「漢文」の場合と、同様である。
平成２７年１２月１２日、毛利太。
（01）
古田島氏が返り点を非論理的だと指摘する根拠は、足りなくなる可能性があるからということらしい。しかし、これは簡単に解決できる。すべて一二点に変換すればいいのである。一二点は無限にあるから、どんなに複雑な構文が出現しても対応できる。実際、一二点しか施していないものも過去にはあった（ブログ：困窮庵日乗）。
（02）
① １ ２ ３ ４ ５ ６ ７ ８ ９
② Ⅰ Ⅱ Ⅲ Ⅳ Ⅴ Ⅵ Ⅶ Ⅷ Ⅸ
③ 一 二 三 四 五 六 七 八 九
は、「数字（アラビア・ローマ・漢）」であって、
①＝②＝③ である。
然るに、
（03）
① ９ ８ ６ ３ ２ １ ５ ４ ７ ＝
① ９〈８｛６［３〔２（１）〕５（４）］７｝〉
に於いて、
① ２（ ）⇒（ ）１
① ３〔 〕⇒〔 〕３
① ５（ ）⇒（ ）５
① ６［ ］⇒［ ］６
① ８｛ ｝⇒｛ ｝８
① ９〈 〉⇒〈 〉９
とするならば、
① 〈｛［〔（１）２〕３（４）５］６７｝８〉９ ＝
① １ ２ ３ ４ ５ ６ ７ ８ ９
加へて、
（04）
② 三 二 Ⅲ ３ ２ １ Ⅱ Ⅰ 一 ＝
② 三〈二｛Ⅲ［３〔２（１）〕Ⅱ（Ⅰ）］一｝〉
に於いて、
② ２（ ）⇒（ ）１
② ３〔 〕⇒〔 〕３
② Ⅱ（ ）⇒（Ⅰ）Ⅱ
② Ⅲ［ ］⇒［ ］Ⅲ
② 二｛ ｝⇒｛ ｝一
② 三〈 〉⇒〈 〉三
とするならば、
② 〈｛［〔（１）２〕３（Ⅰ）Ⅱ］Ⅲ一｝二〉三 ＝
② １ ２ ３ Ⅰ Ⅱ Ⅲ 一 二 三
従って、
（03）（04）により、
（05）
① ９ ８ ６ ３ ２ １ ５ ４ ７ と、
② 三 二 Ⅲ ３ ２ １ Ⅱ Ⅰ 一 は、
① 〈 ｛ ［ 〔 （ ） 〕 （ ） ］ ｝ 〉
② 〈 ｛ ［ 〔 （ ） 〕 （ ） ］ ｝ 〉
を介して、「等しい」。
然るに、
（06）
① １ ２ ３
② Ⅰ Ⅱ Ⅲ
③ 一 二 三
といふ「数字（返り点）」は、
① 一 二 三
② 上 中 下
③ 甲 乙 丙
といふ「返り点（数字）」に、「置き換へ」ることが、出来る。
従って、
（02）（05）（06）により、
（07）
③ 九 八 六 三 二 一 五 四 七 と、
④ 丙 乙 下 三 二 一 中 上 甲 は、
③ 〈 ｛ ［ 〔 （ ） 〕 （ ） ］ ｝ 〉
④ 〈 ｛ ［ 〔 （ ） 〕 （ ） ］ ｝ 〉
を介して、「等しい」。
然るに、
（08）
④ 三 ← 二 ← 一
④ 下 ← 中 ← 上
④ 丙 ← 乙 ← 甲
は、三つとも、「右から左へ、返ってゐる」。
従って、
（09）
「縦書き」であれば、
④ 丙 乙 下 三 二 一 中 上 甲
に於いて、
④ 三 ← 二 ← 一
④ 下 ← 中 ← 上
④ 丙 ← 乙 ← 甲
は、三つとも、「下から上へ、返ってゐる」。
然るに、
（10）
③ 三 ← 二 ← 一
③ 三 → 四
③ 五 ← 四
③ 六 → 七
③ 九 ← 八 ← 七
の場合は、
③ 三 ← 二 ← 一
③ 五 ← 四
③ 九 ← 八 ← 七
に於いて、「右から左へ、返ってゐて」、
③ 三 → 四
③ 六 → 七
に於いて、「左から右へ、返ってゐる」。
従って、
（09）（10）により、
（11）
「縦書き」であれば、
③ 九 八 六 三 二 一 五 四 七
は、「下から上に返ったり、上から下に返ってゐて」、
④ 丙 乙 下 三 二 一 中 上 甲
は、「下から上に返ってゐる」。
然るに、
（12）
④「下から上に返ってゐる。」の方が、
③「下から上に返ったり、上から下に返ってゐる。」よりも、「読みにくい」はずがない。
従って、
（13）
① 一 二 三 四 五 六 七 八 九
よりも、
① 一 二 三
② 上 中 下
③ 甲 乙 丙
の方が、「読みやすい」。
（14）
このことは、
① 〈 ｛ ［ 〔 （ ） 〕 （ ） ］ ｝ 〉
の方が、
① （ （ （ （ （ ） ） （ ） ） ） ）
よりも「読みやすい」ことに、似てゐる。
従って、
（15）
一二点は無限にあるから、どんなに複雑な構文が出現しても対応できる。実際、一二点しか施していないものも過去にはあった（ブログ：困窮庵日乗）。としても、
一二点だけでは、「読みにくい」が故に、今はない。
（16）
⑤ １ １４ １３ ２ １１ ３ ７ ４ ６ ５ ８ １０ ９ １２＝
⑤ １ １４〈１３｛２ １１［３ ７〔４ ６（５）〕８ １０（９）］１２｝〉⇒
⑤ １〈｛２［３〔４（５）６〕７ ８（９）１０］１１ １２｝１３〉１４＝
⑤ １ ２ ３ ４ ５ ６ ７ ８ ９ １０ １１ １２ １３ １４
従って、
（05）（07）（16）により、
（17）
① ９ ８ ６ ３ ２ １ ５ ４ ７
に対して、「返り点」を付けよといふ「問題」は、
⑤ １ １４ １３ ２ １１ ３ ７ ４ ６ ５ ８ １０ ９ １２
に対して、「返り点」を付けよといふ「問題」に、等しい。
ｃｆ.
従って、
（05）（07）（17）により、
（18）
「レ点」がなければ、
⑤ １ １４ １３ ２ １１ ３ ７ ４ ６ ５ ８ １０ ９ １２
に付く「返り点」は、
⑤ 丙 乙 下 三 二 一 中 上 甲
である。
（19）
「レ点」を用ゐれば、
⑤ １ １４ １３ ２ １１ ３ ７ ４ ６ ５ ８ １０ ９ １２
に付く「返り点」は、
⑤ レ 乙 下 二 一レ 上レ 甲
である。
従って、
（20）
① レ
② 一 二 三 四 五 六 七 八 九 ・ ・ ・ ・ ・ ・
③ 上 中 下
④ 甲 乙 丙 丁 戊 己 庚 辛 壬
⑤ 天 地 人
の「代はり」に、
① １ ２ ３ ４ ５ ６ ７ ８ ９
② Ⅰ Ⅱ Ⅲ Ⅳ Ⅴ Ⅵ Ⅶ Ⅷ Ⅸ
③ 一 二 三四 五 六 七 八 九
④ 甲 乙 丙 丁 戊 己 庚 辛 壬
を「返り点」とすることが、出来る。
（21）
① １ ２ ３ ４ ５ ６ ７ ８ ９
② Ⅰ Ⅱ Ⅲ Ⅳ Ⅴ Ⅵ Ⅶ Ⅷ Ⅸ
③ 一 二 三 四 五 六 七 八 九
④ 甲 乙 丙 丁 戊 己 庚 辛 壬
は、それぞれが、「数字」であるが、
① ② ③ ④
も、「数字」である。
従って、
（21）により、
（22）
① １ ２ ３ ４ ５ ６ ７ ８ ９
② Ⅰ Ⅱ Ⅲ Ⅳ Ⅴ Ⅵ Ⅶ Ⅷ Ⅸ
③ 一 二 三 四 五 六 七 八 九
④ 甲 乙 丙 丁 戊 己 庚 辛 壬
は、「数字の中」に、「数字」が入ってゐる。
然るに、
（23）
こういうロシアの入れ子人形のような性質を、コンピューター科学や言語学、心理学、哲学などではリカージョンと呼ぶ（ピダハン、３１７頁）。
従って、
（20）（22）（23）により、
（24）
「返り点」は、「リカージョン」である。
然るに、
（25）
① 〈 ｛ ［ 〔 （ ） 〕 （ ） ］ ｝ 〉
① （ （ （ （ （ ） ） （ ） ） ） ）
は、「入れ子」である。
従って、
（23）（25）により、
（26）
「括弧」も、「リカージョン」である。
平成２７年１１月２７日、毛利太。
（01）
（２）「未」は「いまダ～ズ」とよみ、「まだ～しない」の意で、「尚不」と同じである。
（中沢希男、 渋谷玲子、漢文訓読の基礎、９０頁）
（02）
（７）比況と呼応するもの。
そのみさをあたかも（チョウド）天上の客の如し。（日本霊異記）
（代々木ゼミ方式 受験国文法、1980年、２０頁）
（03）
【恰】① あたかも。ちょうど。
（旺文社、高校基礎漢和辞典、1984年、３４９頁）
（04）
【猶】②「なお～ごとし」とよみ「ちょうど～のようだ」と訳す。再読文字。
（改定新版、漢字源、1988年、973頁）
（05）
【蓋】［二］漢文で「なんぞ ・ ・ ・ ・ ・ ・ せざる」と返って読み、「どして ・ ・ ・ ・ ・ ・ しないのか」の意。蓋ｶﾌの音が何不ｶﾌに通ずるのでいう。（同）盍ｺｳ（角川漢和中辞典、1959年、９４３頁）
従って、
（01）～（05）により、
（06）
「未」は「いまだ～ず」 と読み、「尚不」と同じである。
「尚」は「なほ～ごとし」と読み、「恰如」と同じである。
「盍」は「なんぞ～ざる」と読み、「何不」と同じである。
然るに、
（07）
「将」は「まさに～す」と読むものの、
「将」＝「囗為」に当たる「囗」が、見つからない。
そのため、
（08）
以下では、仮に、
「将」＝「且為」と、する。
従って、
（08）により、
（09）
吾将任彼而不用吾力焉＝
吾且為［任（彼）而不〔用（吾力）〕］焉⇒
吾且［（彼）任而〔（吾力）用〕不］為焉＝
吾且に［（彼に）任せて〔（吾が力を）用ゐ〕不らんと］す。
であるが、この場合、而は「接続詞」、焉 は、「置き字」である。
従って、
（09）により、
（10）
吾将任彼而不用吾力焉。
に付く「括弧」は、
［ （ ）〔 （ ） 〕 ］
だけであって、他には無い。
然るに、
（11）
丁［二（一）丙〔乙（甲）〕］。
に於いて、
二（一）⇒（二）一
乙（甲）⇒（乙）甲
丙〔 〕⇒〔 〕丙
丁［ ］⇒［ ］丁
とするならば、
丁［二（一）丙〔乙（甲）〕］⇒
［（一）二〔（甲）乙〕丙］丁＝
一 二 甲 乙 丙 丁。
従って、
（10）（11）により、
（12）
［ （ ）〔 （ ） 〕 ］
といふ「括弧」は、
丁 二 一 丙 乙 甲
といふ「返り点」に、相当する。
然るに、
（13）
任（彼）⇒
（彼に）任す。
の場合は、「一字だけ」返ってゐる。
然るに、
（14）
大辞林 第三版の解説
れてん【レ点】
漢文訓読に用いる返り点の一。一字だけ返って読むという符号。「読レ書（書ヲ読ム）」「不レ明（明ラカナラズ）」の「レ」の類。かりがね点。
（10）～（14）により、
（15）
吾将任彼而不用吾力焉。
に付く「返り点」は、
丁 二 一 丙 乙 甲
ではなく、
四 レ 三 二 一
でなければ、ならない。
然るに、
（16）
従って、
（12）（15）（16）により、
（17）
吾将任彼而不用吾力焉。
に付く「括弧」は、
［ （ ）〔 （ ） 〕 ］
だけであって、他には無いものの、
吾将任彼而不用吾力焉。
に付く「返り点」は、
四 レ 三 二 一
丁 二 一 丙 乙 甲
二 レ 一レ 二 一
下 レ 上レ 二 一
による、「四通り」が、有り得る。ことになる。
― 話は変はって、―
（18）
今の日本の中学・高校では英語・数学・国語を主要３教科と呼んでいますが、戦前、旧制の中学では英語・数学・国語・漢文が主要４教科でした。漢文は国語とは独立した教科だったんですね。読解はもとより、復文（書き下し文から原文を復元）や作文もやるし、これだけ高度な学習内容でしたから、白文の読解もなんのそのでした。しかし戦後、漢文は国語の一部である古典分野の、そのまた片隅に追いやられてしまいました。漢文の得意な教師は少なく、漢文に興味を持つ生徒も少なく、おまけに最近は大学入試科目から漢文が消えつつあるので、みんないやいやながら学んでいます。内容もたいしたことはなく、学者先生が返り点と送り仮名をつけた文章をえっちらおっちら読む程度です（Ｗｅｂサイト：漢文入門）。
（19）
本書は曩に世に公にした『国文解釋法』の姉妹編であつて、やはり諸官立學校の入學受驗準備を主要な目的として書いた本である。― 中略 ― あらゆる既知未知の問題 ― それもあまり高尚難澁でない問題に對して、白文に句讀訓點を施し、且つその文の大意が間違ひなく取れるだけの力がつけば、諸君の漢文受驗に對する豫備は十中八九は既に成つたものである。
（塚本哲三、漢文解釋法、1917年、緒言）
従って、
（18）（19）により、
（20）
大正の（国公立校の）受験生は、「白文」に対して、自分で「返り点」を付けるだけの実力が要求されてゐたのに対して、平成の高校の先生は、「学者先生が返り点と送り仮名をつけた文章を読む程度」の実力しか、期待されゐない。
ｃｆ.
純粋な白文というのは句点（。）も読点（.，）も全くなく，それこそ漢字が何十も何百も切れ目なく続いている漢文のことをいいます。白文が読めるようになるというのは，まず正確に句点や読点を打つことが出来るということです。この段階で，本当に漢文の出来る人と，そうではない人が分かります。その上で，正確に返り点や送り仮名をつけて訓読が出来るということです。一般の人であれば，句読点の全くない白文はまず無理であって，句読点のついた白文が読めるようになるだけでも大したものです（ohirune_daisukeさん 2010/1/2314:58:25）。
平成２７年１１月２５日、毛利太。
（01）
まったく【全く】（副）〔雅語。「またく」の強調形〕そうとしか形容できないほど強く感じることを表す。「―〔＝いかなる意味においても・（全然）〕忘れていた・―〔＝実に〕つらい話だ・―〔＝お世辞抜きで〕うまいね・これは ― の幸運だった」〔元来は、否定表現を伴った〕
（新明解国語辞典 第四版、1991年、１２２２頁）
従って、
（01）により、
（02）
まったく【全く】（副）は、〔元来は、否定表現を伴った〕。
然るに、
（03）
たえて【絶えて】〔副〕①〔下に打消の語を伴って〕まったく（～ない）。全然（～ない）。
（古語林、1997年、８０２頁）
加へて、
（04）
（三）叙述の副詞（副詞の呼応）あるきまった語と呼応して意味の述べ方を助けるもの。
（１）打消（禁止）と呼応するもの。
― 中略、―
心やましきさまにたえて（ゼンゼン・マッタク）ことづてもなし（蜻蛉日記）
（代々木ゼミ方式 受験国文法、1980年、１７・１８頁）
従って、
（02）（03）（04）により、
（05）
「全く＝全然＝絶えて」は、「打消（禁止）」と呼応する「呼応の副詞」である。
然るに、
（06）
① 少しも食べる。
② 少しは食べる。
③ 少しも食べない。
に於いて、
① 少しも食べる。
といふ「日本語」は、無い。
従って、
（05）（06）により、
（07）
③ 少しも食べない。
に於ける、
③ 少しも
は、「打消（禁止）」と呼応する「呼応の副詞」である。
従って、
（05）（07）により、
（08）
③ 絶不（食）⇒
③ 絶へて（食せ）不＝
③ 少しも（食べ）ない。
に於いて、
③ 絶
は、
③ 不
に「係ってゐる」と、すべきである。
然るに、
（09）
③ 不（食）⇒
③ （食せ）不＝
③ （食べ）ない。
に於いて、
③ 不
は、
③ 食
に「係ってゐる」と、すべきである。
従って、
（08）（09）により、
（10）
③ 絶不（食）⇒
③ 絶へて（食せ）不＝
② 少しも（食べ）ない。
に於いて、
③ 絶 は 不 に「係ってゐて」、
③ 不 は 食 に「係ってゐる」。 が故に、
③ 絶不 は 食 に「係ってゐる」と、すべきである。
従って、
（10）により、
（11）
④ 何不（食）⇒
④ 何ぞ（食らは）不る＝
④ どうして （食べ）ないのか。
に於いて、
④ 何不 は 食 に「係ってゐる」と、すべきである。
然るに、
（12）
【盍】コウ（カフ）②〔盍 ・ ・ ・ ・ ・ ・〕（再読文字）「なんゾ ・ ・ ・ ・ ・ ・ざル」と読み、「どうして ・ ・ ・ ・ ・ ・ しないのか、 ・ ・ ・ ・ ・ ・ すればよいではないか」の意。「何不 ・ ・ ・ ・ ・ ・ 」と同じで「何不ｶﾌ」の二音が「盍ｶﾌ・ｺｳ」の一音につまったもので「蓋」と同じに用いる（旺文社、高校基礎漢和辞典、1984年、５５８頁）。
従って、
（11）（12）により、
（13）
④ 盍（食）⇒
④ 何ぞ（食らは）不る＝
④ どうして （食べ）ないのか。
に於いて、
④ 盍＝何不 は 食 に「係ってゐる」と、すべきである。
従って、
（10）～（13）により、
（14）
④ なんぞ・ざる＝何不＝盍
のやうに、
③ たへて・ず ＝絶不＝囗
に相当する、
③ 囗
といふ「漢字」が有るのであれば、
③ 囗
といふ「漢字」は、「盍」と同じく、「再読文字」であるが、
③ 絶不＝囗
に相当する、
③ 囗
といふ「漢字」は無い。
然るに、
（15）
（４）当然（命令）と呼応するもの。
なんぢまさに知るべし。（オ前ハ当然知ラナケレバナラナヌ）（今昔物語）
徳をつかんと思はばすべからくまづその心づかいを修業すべし（徳ヲツモウト思ッタラ当然ナスベキコトトシテ、マズソノ心ﾉ使イ方ヲ修業シナケレバナラヌ）（徒然草）
（代々木ゼミ方式 受験国文法、1980年、１９頁）
従って、
（14）（15）により、
（16）
⑤ マサニ ・ ・ ・ ・ ・ スベシ。
⑥ スベカラク ・ ・ ・ ・ ・ スベシ。
に相当する、
⑤ 囗
⑥ 囗
といふ「漢字」があれば、それらの「漢字」は、「日本語」から見れば、
⑤ 囗＝呼応の副詞＋助動詞。
⑥ 囗＝呼応の副詞＋助動詞。
といふ「形」をしてゐることになる。
然るに、
（17）
７ 再読文字
当 まさニ ・ ・ ・ ・ ・ スベシ。
宜 よろシク ・ ・ ・ ・ ・ スベシ。
（鳥羽田重直、漢文の基礎、1985年、２５頁改）
（１）「未」「將」「當」「應」「宜」「須」「猶」「盍」などの諸字は、一字でありながら、最初副詞によみ、次に動詞あるいは助動詞によむのが例になっている。
（中沢希男、 渋谷玲子、漢文訓読の基礎、９０頁）
従って、
（16）（17）により、
（18）
「日本語」から見たとき、「再読文字」は、その「意味」として、「呼応の副詞」を含んでゐる。
平成２７年１１月２３日、毛利太。
― 「１１月１６日の記事」を書き換へます。―
（01）
登門＝門に登る。
の「返り点」は、
レ
である。
然るに、
（02）
登竜門＝竜門に登る。
に於いて、
竜‐門 を、ハイフンで結んで、
竜‐門 とすると、
従って、
（03）
師‐事 を、ハイフンで結んで、
師‐事 とするならば、
欲師‐事之＝之に師‐事せんと欲す。
の「返り点」は、
レ
レ
で表すことが、出来る。
然るに、
（04）
従って、
（03）（04）により、
（05）
欲師事之＝之に師事せんと欲す。
に対する「返り点」は、
といふ「五通り」が可能であるものの、古田島先生の説明によれば、
④ だけが、「正しい」。
然るに、
（06）
欲〔師事（之）〕。
に於いて、
師‐事（ ）⇒（之）師‐事
師‐欲〔 〕⇒〔 〕欲
とするならば、
欲〔師‐事（之）〕⇒
〔（之）師‐事〕欲＝
〔（之に）師‐事せんと〕欲す。
従って、
（07）
欲師‐事之＝之に師‐事せんと欲す。
に対する「括弧」は、
欲〔師事（之）〕。
欲〔師‐事（之）〕。
といふ、「二通り」しかない。
（08）
欲師事之。
といふ「漢文」自体は、少なくとも、「表面的（surface structure的）」には、
欲〔師‐事（之）〕。
といふ「形」をしてゐない。
然るに、
（09）
欲師事之＝之に師事せんと欲す。
といふ「訓読」が「正しい」限り、
欲＝欲す。
が、
師事之＝之に師事せんと
に「係ってゐる」こと、並びに、
師事＝師事す
が、
之＝之に
に「係ってゐる」ことは、「明白」である。
然るに、
（10）
欲
が、
師事之
に「係ってゐて」、
師事
が、
之
に「係ってゐる」のであれば、
欲師事之＝
欲〔師事（之）〕。
とすることに、「不都合」は、無い。
（11）
He said, "I am a Japanese."
の「英訳（ヤフー！翻訳）」は、
「私は、日本人です。」と、彼は言いました。
である。
従って、
（12）
彼曰我日本人也＝彼曰く我は日本人なりと。
であっても、
彼曰「我日本人也」＝彼曰く「我は日本人なり」と。
といふ風に、「括弧」で括っても、「不都合」は無い。
然るに、
（13）
Why not ask him his nationality?
といふ英語は、
「 彼に彼の国籍を尋ねること」を、促してゐる。
従って、
（13）により、
（14）
Why not ask him his nationality?
といふ英語は、
Why not「ask him his nationality」.
といふ風に、解することが、出来る。
然るに、
（15）
【盍】コウ（カフ）②〔盍 ・ ・ ・ ・ ・ ・〕（再読文字）「なんゾ ・ ・ ・ ・ ・ ・ざル」と読み、「どうして ・ ・ ・ ・ ・ ・ しないのか、 ・ ・ ・ ・ ・ ・ すればよいではないか」の意。「何不 ・ ・ ・ ・ ・ ・ 」と同じで「何不ｶﾌ」の二音が「盍ｶﾌ・ｺｳ」の一音につまったもので「蓋」と同じに用いる（旺文社、高校基礎漢和辞典、1984年、５５８頁）。
従って、
（15）により、
（16）
盍＝何不＝ＷｈｙＮｏｔ
である。
従って、
（14）（16）により、
（17）
Why not「ask him his nationality」＝
何不「ask him his nationality」＝
何不「問彼之国籍於彼」。
といふ風に、解することが、出来る。
従って、
（12）（17）により、
（18）
曰 ・ ・ ・ ・ ・ ・
何不 ・ ・ ・ ・ ・ ・
に関しては、
曰（ ・ ・ ・ ・ ・ ・ ）
何不（ ・ ・ ・ ・ ・ ・ ）
といふ風に、解することが、出来る。
然るに、
（19）
何不令人謂韓公叔曰秦之敢絶周而伐韓者信東周也公何不与周地発質使之楚秦必疑楚不信周是韓不伐也又謂秦曰韓彊与周地将以疑周於秦也周不敢不受。
といふ「一つの漢文」に関して、次の通りである。
（20）
「通常の包含関係」といふのは、
① 一 二 三 四 五 六 七 八 九 十 ・ ・ ・ ・ ・ ・
② 上 中 下
③ 甲 乙 丙 丁 戊 己 庚 辛 壬 癸
④ 天 地 人
に於いて、
④ の間に、③ が入り、
③ の間に、② が入り、
② の間に、① が入ることを、いひ、それ故、
（21）
④ 天 地 人
ではなく、
④ 天 地 人 間
であるならば、
レ 丁 二 一 地 レ レ 二 一 下 二 一 二 一 上レ レ レ レ 天レ レ 丙 二 一 三 二 一 乙 甲レ
といふ「それ」は、
レ 間 二 一 乙 レ レ 二 一 下 二 一 二 一 上レ レ レ レ 甲レ レ 人 二 一 三 二 一 地 天レ
でなければ、ならない。
然るに、
（22）
従って、
（17）（18）（22）により、
（23）
何不〈令｛人謂（韓公叔）曰［秦之敢絶（周）而伐（韓）者、信（東周）也、公何不〔与（周地）発（質使）之（楚）〕、秦必疑（楚）、不〔信（周）〕、是韓不（伐）也］、又謂（秦）曰、［韓彊与（周地）、将〔以疑（周於秦）〕也、周不〔敢不（受）〕］｝〉。
といふ「括弧」の内の、少なくとも、
曰［ ・ ・ ・ ・ ・ ・ ］
曰［ ・ ・ ・ ・ ・ ・ ］
何不〔 ・ ・ ・ ・ ・ ・ 〕
何不〈 ・ ・ ・ ・ ・ ・ 〉
といふ「括弧」、すなはち、
Ｓａｙ［ ・ ・ ・ ・ ・ ・ ］
Ｓａｙ［ ・ ・ ・ ・ ・ ・ ］
ＷｈｙＮｏｔ〔 ・ ・ ・ ・ ・ ・ 〕
ＷｈｙＮｏｔ〈 ・ ・ ・ ・ ・ ・ 〉
といふ「括弧」に関しては、それらが、無いはずがない。
（24）
これまでに、繰り返し述べて来たやうに、
漢語における語順は、国語と大きく違っているところがある。その補足構造における語順は、国語とは全く反対である（鈴木直治著、中国語と漢文、1975年、２９６頁）。
従って、
（23）（24）により、
（25）
何不〈 ・ ・ ・ ・ ・ ・ 〉。
の不 が、
〈 ・ ・ ・ ・ ・ ・ 〉
を「補語」とするとき、「日本語」では、
何〈 ・ ・ ・ ・ ・ ・ 〉不。
といふ「語順」になる。
従って、
（26）
何不〈令｛・ ・ ・ ・ ・｝ 〉。
の不 が、
〈令｛ ・ ・ ・ ・ ・｝〉
を「補語」とし、
令｛ ・ ・ ・ ・ ・｝
の令 が、
｛ ・ ・ ・ ・ ・｝
を「補語」とするとき、「日本語」では、
何不〈令｛・ ・ ・ ・ ・｝〉。
何〈｛・ ・ ・ ・ ・｝令〉不＝
何ぞ〈｛・ ・ ・ ・ ・｝令め〉ざる。
といふ風に、読むことになる。
従って、
（24）（25）（26）により、
（27）
何不令人謂韓公叔曰秦之敢絶周而伐韓者信東周也公何不与周地発質使之楚秦必疑楚不信周是韓不伐也又謂秦曰韓彊与周地将以疑周於秦也周不敢不受。
といふ「漢文」に、
（28）
何不〈令｛人謂（韓公叔）曰［秦之敢絶（周）而伐（韓）者、信（東周）也、公何不〔与（周地）発（質使）之（楚）〕、秦必疑（楚）、不〔信（周）〕、是韓不（伐）也］、又謂（秦）曰、［韓彊与（周地）、将〔以疑（周於秦）〕也、周不〔敢不（受）〕］｝〉。
といふ「補足構造」が有るとき、「日本語」では、
（29）
何ぞ〈｛人をして（韓の公叔に）謂ひて［秦の敢へて（周を）絶って（韓を）伐んとするは、（東周を）信ずればなり、公何ぞ〔（周に地を）与へ（質使を）発して（楚に）之かしめ〕ざる、秦必ず（楚を）疑ひ、〔（周を）信ぜ〕ざらん、是れ韓（伐たれ）ざらんと］曰ひ、又（秦に）謂ひて、［韓彊ひて（周に地を）与ふるは、将に〔以て（周を秦に）疑はしめんとする〕なり、周〔敢へて（受け）ずんば〕あらずと］曰は｝令め〉ざる。
といふ風に、読むことになる。
従って、
（30）
「換言」すると、
何不〈令｛人謂（韓公叔）曰［秦之敢絶（周）而伐（韓）者、信（東周）也、公何不〔与（周地）発（質使）之（楚）〕、秦必疑（楚）、不〔信（周）〕、是韓不（伐）也］、又謂（秦）曰、［韓彊与（周地）、将〔以疑（周於秦）〕也、周不〔敢不（受）〕］｝〉。
といふ「補足構造」が有るからこそ、
（31）
何不令人謂韓公叔曰秦之敢絶周而伐韓者信東周也公何不与周地発質使之楚秦必疑楚不信周是韓不伐也又謂秦曰韓彊与周地将以疑周於秦也周不敢不受。
といふ「漢文」は、
（32）
何ぞ〈｛人をして（韓の公叔に）謂ひて［秦之敢へて（周を）絶つ而（韓を）伐んとする者、（東周を）信ずれば也、公何ぞ〔（周に地を）与へ（質使を）発して（楚に）之かしめ〕不る、秦必ず（楚を）疑ひ、〔（周を）信ぜ〕不らん、是れ韓（伐たれ）不らん也と］曰ひ、又（秦に）謂ひて、［韓彊ひて（周に地を）与ふるは、将に〔以て（周を於秦に）疑はしめんとする〕也、周〔敢へて（受け）不んば〕不ずと］曰は｝令め〉不る。
といふ風に、「訓読」出来る。ことになる。
従って、
（30）（31）（32）により、
（33）
何不令人謂韓公叔曰秦之敢絶周而伐韓者信東周也公何不与周地発質使之楚秦必疑楚不信周是韓不伐也又謂秦曰韓彊与周地将以疑周於秦也周不敢不受。
に付く、
レ 丁 二 一 地 レ レ 二 一 下 二 一 二 一 上レ レ レ レ 天レ レ 丙 二 一 三 二 一 乙 甲レ
といふ「返り点」は、
（34）
〈 ｛ （ ） ［ （ ）（ ）（ ） 〔 （ ）（ ）（ ） 〕 （ ） 〔 （ ） 〕 （ ） ］ （ ） ［ （ ） 〔 （ ） 〕 〔 （ ） 〕 ］ ｝ 〉
といふ「補足構造」に、附いてゐる。ことになる。
従って、
（35）
仮に、我々の先人が、「漢文訓読」を行はなかったとしても、
何不令人謂韓公叔曰秦之敢絶周而伐韓者信東周也公何不与周地発質使之楚秦必疑楚不信周是韓不伐也又謂秦曰韓彊与周地将以疑周於秦也周不敢不受。
といふ「漢文」には、
〈 ｛ （ ） ［ （ ）（ ）（ ） 〔 （ ）（ ）（ ） 〕 （ ） 〔 （ ） 〕 （ ） ］ （ ） ［ （ ） 〔 （ ） 〕 〔 （ ） 〕 ］ ｝ 〉
といふ「括弧」が有る。ことになる。
従って、
（01）～（35）により、
（36）
括弧不可不有（括弧はあります）。
平成２７年１１月１８日、毛利太。
（01）
① 我読書。
を、
① 我書読。
とした上で、
② 書
を、
② 所
に替へると、
② 我所読（我の読む所）＝書
となる。
（02）
この時、
② 我所読（我の読む所）＝書
であると同時に、
② 所読（読む所）＝書
② 所読書（読む所の書）＝書
② 所読者（読む所の者）＝書
② 我所読書（我の読む所の書）＝書
② 我所読者（我の読む所の者）＝書
である。
従って、
（01）（02）により、
（03）
① 我読書（我、書を読む）。
であれば、
② 我所読書（我の読む所の書）＝書
であるものの、
②「我」は、「省略可能」であって、
②「書」も、「省略可能」であり、
②「書」は、「者」に、「置き換へ可能」である。
（04）
客有教燕王為不死之道者。王使人学之。所使学者、未及学而客死。
客に燕王に教へて不死の道をなす者有り。王、人をして之を学ばしむ。学ばしむる所の者、未だ学ぶに及ばずして客死せり。
食客中、燕の王に不老不死の方法を教える者がいた。王は人に命じて方法を学ばせた。学ばせた者がまだ学び終わらないうちにその人が死んだ（多久弘一、多久の漢文公式１１０、1998
年、１３頁）。
然るに、
（05）
「教」は教えてさせる意（鳥羽田重直、漢文の基礎、1985年、４９頁）であるため、
客有教燕王不死之道者＝
客に燕王に教へて不死の道をなす者有り。
ではなく、
客有教燕王不死之道者。
客に燕王に教へて不死の道をなさしむ者有り。
とすべきである。
従って、
（04）（05）により、
（06）
１ｓｔ： 客が、王にさうするやうに、すすめて、
２ｎｄ： 王が、人にさうするやうに、命じて、
３ｒｄ： 人が、不死の道を、学んだことになる。
従って、
（03）（06）により、
（07）
王使人学之。所使学者、
であれば、
所使学者（学ば使むる所の者）＝
王所使学之者（王の之を学ば使むる所の者）＝人
である。
従って、
（04）～（07）により、
（08）
所使学者未及学而客死＝
学ば使むる所の者未だ学ぶに及ばずして客死せり。
といふ漢文は、「正確」には、
王所使学不死之道者未及学不死之道而客死＝
王所［使〔学（不死之道）〕］者未［及〔学（不死之道）〕］而客死 ⇒
王［〔（不死之道）学〕使］所者未［〔（不死之道）学〕及］不而客死 ＝
王の［〔（不死の道を）学ば〕使むる］所の者未だ［〔（不死の道を）学ぶに〕及ば］不して而客死せり ＝
王が［〔（不死の道を）学ば〕せた］その人がまだ［〔（不死の道を）学んで〕ゐ］ないのに、客は死んでしまった。
といふ、ことになる。
（09）
客有教燕王不死之道者。王使人学之。所使学者未及学而客死。
といふ漢文を、初めて読んだ時、私は、「所使学者」の意味が、よく分からなかった。
平成２７年１１月０４日、毛利太。
（01）
「返り点」とは、「縦書き」であれば、「下から上へ返る、返り点」であって、それ故、
「返り点」とは、「横書き」であれば、「右から左へ返る、返り点」である。
従って、
（01）により、
（02）
「返り点」とは、「横書き」であれば、「右から左へ返る、返り点」であって、それ故、
「返り点」とは、「横書き」であれば、「左から右へ返る、返り点」ではない。
従って、
（02）により、
（03）
β ： ２←１
α ： ３←２
ε ： ３←２←１
のやうな「順序」でなければ、「返り点」は付かない。
従って、
（03）により、
（04）
α ： １ ３ ２
β ： ２ １ ３
γ ： ２ ３ １
δ ： ３ １ ２
ε ： ３ ２ １
であれば、
α ： 囗 ３ ２
β ： ２ １ 囗
γ ： ２ 囗 １
δ ： ３ 囗 ２
ε ： ３ ２ １
とした場合、「返り点」は、「囗の位置」には、付かない。
然るに、
（05）
γ ： ２ 囗 １
といふ「順番」に付く「返り点」は、
① 二 囗 一
である。
然るに、
（06）
① 二 囗 一
に於いて、
① 「最初に」読まれる「それ」を、「＃」とすると、
① 二 ＃ 一
である。
ｃｆ.
従って、
（06）により、
（07）
① 二 囗 一
といふ「返り点」を、
① ２ ３ １
の「順」で読まうとすれば、その場合は、
① 二 三 一
とせざるを得ない。
然るに、
（08）
① 二 三 一
であれば、
① 二→三
であるため、「左から右」へ「返ってゐる」。
従って、
（02）（08）により、
（09）
① 二 三 一
といふ「返り点」は、存在しない。
従って、
（07）（08）（09）により、
（10）
「返り点」は、
① ２ ３ １
といふ「順番」に、付くことが、出来ない。
（11）
② 二 三 囗 一
であれば、
② 二 三 ＃ 一
である。
然るに、
（12）
② 二 三 ＃ 一
であれば、
② ＃→一→二→三
従って、
（11）（12）により、
（13）
② 二 三 囗 一
といふ「それ」を、
② ２ ３ ４ １
の「順」で読まうとすれば、その場合は、
② 二 三 四 一
とせざるを得ない。
然るに、
（14）
② 二 三 四 一
であれば、
② 二→三→四
であるため、「左から右」へ「返ってゐる」。
従って、
（02）（14）により、
（15）
② 二 三 四 一
といふ「返り点」は、存在しない。
従って、
（13）（14）（15）により、
（16）
「返り点」は、
② ２ ３ ４ １
といふ「順番」に、付くことが、出来ない。
（17）
③ 二 囗 三 一
であれば、
③ 二 ＃ 三 一
である。
然るに、
（18）
③ 二 ＃ 三 一
であれば、
③ ＃→一→二→三
従って、
（17）（18）により、
（19）
③ 二 囗 三 一
といふ「それ」を、
③ ２ ４ ３ １
の「順」で読まうとすれば、その場合は、
③ 二 四 三 一
とせざるを得ない。
然るに、
（20）
③ 二 四 三 一
であれば、
③ 二→三
であるため、「左から右」へ「返ってゐる」。
従って、
（02）（20）により、
（21）
③ 二 四 三 一
といふ「返り点」は、存在しない。
但し、
（22）
然るに、
（23）
〔説明〕二つの返り点がいっしょになるのは、一とレ、上とレ、甲とレ、天とレの四つだけである（志村和久、漢文早やわかり、1982年、１８頁）。
従って、
（21）（22）（23）により、
（24）
③ 二 四 三 一
③ 二 三レ 一
といふ「返り点」は、存在しない。
従って、
（19）～（24）により、
（25）
「返り点」は、
③ ２ ４ ３ １
といふ「順番」に、付くことが、出来ない。
従って、
（10）（16）（25）により、
（26）
「返り点」は、
① ２ ３ １
② ２ ３ ４ １
③ ２ ４ ３ １
といふ「順番」に、付くことが、出来ない。
然るに、
（27）
④ 中 二 一 下 二 一 上
であれば、
④ 六 二 一 七 四 三 五
然るに、
（28）
④ 六 二 一 七 四 三 五
であれば、
④ 二→三
④ 四→五
④ 六→七
である。
然るに、
（29）
④ 中 二 一 下 二 一 上
であるため、
④ 中 二 一 下 四 三 上
であっても、
④ 中 二 一 下
④ 下 四 三 上
の「二 一」と、「四 三」は、別々の、異なる「一二点」である。
加へて、
（30）
④ 四 五
であっても、
④ 二 上
は、一方は、「一二点」であって、一方は「上下点」である。
従って、
（27）～（30）により、
（31）
④ 中 二 一 下 二 一 上
④ 六 二 一 七 四 三 五
であれば、
④ 中→下
④ 六→七
であるため、「左から右」へ「返ってゐる」。
従って、
（02）（31）により、
（32）
④ 中 二 一 下 二 一 上
といふ「返り点」は、存在しない。
従って、
（27）（31）（32）により、
（33）
「返り点」は、
④ ６ ２ １ ７ ４ ３ ５
といふ「順番」に、付くことが、出来ない。
（10）（16）（25）（33）により、
（34）
「返り点」は、
① ２ ３ １
② ２ ３ ４ １
③ ２ ４ ３ １
④ ６ ２ １ ７ ４ ３ ５
といふ「順番」に、付くことが、出来ない。
然るに、
（35）
① ２ ３ １
② ２ ３ １
③ ２ ４ １
④ ６ ７ ５
といふ「それ」は、
① Ｌ＜Ｍ＞Ｎ ＆ Ｌ＝Ｎ＋１
② Ｌ＜Ｍ＞Ｎ ＆ Ｌ＝Ｎ＋１
③ Ｌ＜Ｍ＞Ｎ ＆ Ｌ＝Ｎ＋１
④ Ｌ＜Ｍ＞Ｎ ＆ Ｌ＝Ｎ＋１
といふ「不等式」を、満たしてゐる。
然るに、
（36）
① ２→３
② ２→３
③ ２→４
④ ６→５
従って、
（35）（36）により、
（37）
① ２→３
② ２→３
③ ２→４
④ ６→５
といふ、「左から右へ」が生じる「所以」は、
① Ｌ＜Ｍ＞Ｎ ＆ Ｌ＝Ｎ＋１
といふ「不等式」に、他ならない。
然るに、
（38）
① ２（３〔１）〕
② ２（３〔４［１）〕］
③ ２（４［３〔１）〕］
④ ６〔２（１）７［４（３）５〕］
に於いて、
① ２（ ）⇒（ ）１
① ３〔 〕⇒〔 〕３
② ２（ ）⇒（ ）１
② ３〔 〕⇒〔 〕３
② ４［ ］⇒［ ］４
③ ２（ ）⇒（ ）１
③ ３〔 〕⇒〔 〕３
③ ４［ ］⇒［ ］４
④ ２（ ）⇒（ ）１
④ ４（ ）⇒（ ）４
④ ６〔 〕⇒〔 〕６
④ ７［ ］⇒［ ］７
とすると、
① （〔１）２〕３
② （〔［１）２〕３］４
③ （［〔１）２〕３］４
④ 〔（１）２［（３）４５〕６］７
然るに、
（39）
① （ ）
② 〔 〕
に於いて、
② が有る場合は、② の中には、一つ以上の ① が有って、
① の中には、① が無いならば、その時に限って、「括弧」とする。
従って、
（39）により、
（40）
① （ 〔 ） 〕
② （ 〔 ［ ） 〕 ］
③ （ ［ 〔 ） 〕 ］
④ 〔（ ）［ （ ） 〕 ］
は、「括弧」ではない。
従って、
（34）（37）（38）（40）により、
（41）
① Ｌ＜Ｍ＞Ｎ ＆ Ｌ＝Ｎ＋１
といふ「順番」を含む、
① ２ ３ １
② ２ ３ ４ １
③ ２ ４ ３ １
④ ６ ２ １ ７ ４ ３ ５
といふ「順番」に対して、「返り点・括弧」は、付くことが、出来ない。
然るに、
（42）
① Ｌ＜Ｍ＞Ｎ ＆ Ｌ＝Ｎ＋１
ではなく、
① Ｌ＜Ｍ＜Ｎ
であれば、例へば、
① １＜２＜３
であるため、初めから、「返り点」は「不用」である。
（43）
① Ｌ＜Ｍ＞Ｎ ＆ Ｌ＝Ｎ＋１
ではなく、
① Ｌ＞Ｍ＜Ｎ
であれば、例へば、
① ２＞１＜３
であるため、
① ２（１）３⇒
① （１）２３＝
① １ ２ ３。
（44）
① Ｌ＜Ｍ＞Ｎ ＆ Ｌ＝Ｎ＋１
ではなく、
② Ｌ＞Ｍ＞Ｎ
であれば、例へば、
② ４＞３＞２
であるため、
② ４〔３（２）〕⇒
② 〔（２）３〕４＝
② ２ ３ ４。
従って、
（42）（43）（44）より、
（45）
① ３ １ ２
② ２ １ ３ ４
③ ４ ３ １ ２
④ ２ １ ７ ４ ３ ５ ６
のやうに、
① Ｌ＜Ｍ＞Ｎ ＆ Ｌ＝Ｎ＋１
ではなければ、
① ３（１ ２）
② ２（１）３ ４
③ ４〔３（１ ２）〕
④ ２（１）７〔４（３）５ ６〕
のやうに、「括弧」を付けることが出来、尚且つ、
① ３（１ ２）
② ２（１）３ ４
③ ４〔３（１ ２）〕
④ ２（１）７〔４（３）５ ６〕
に対する「返り点」は、
① 二 一
② レ
③ レ 二 一
④ レ 二 レ 一
である。
ｃｆ.
従って、
（41）（45）により、
（46）
① Ｌ＜Ｍ＞Ｎ ＆ Ｌ＝Ｎ＋１
といふ「順番」を含む、
① ２ ３ １
② ２ ３ ４ １
③ ２ ４ ３ １
④ ６ ２ １ ７ ４ ３ ５
といふ「順番」に対して、「返り点・括弧」は、付くことが、出来ない一方で、
① Ｌ＜Ｍ＞Ｎ ＆ Ｌ＝Ｎ＋１
といふ「順番」を含まない、
① ３ １ ２
② ２ １ ３ ４
③ ４ ３ １ ２
④ ２ １ ７ ４ ３ ５ ６
といふ「順番」に対しては、「返り点・括弧」を、付けることが、出来る。
然るに、
（47）
「返り点」とは、「縦書き」であれば、「下から上へ返る、返り点」であって、それ故、
「返り点」とは、「横書き」であれば、「右から左へ返る、返り点」である。
とするならば、以上の「理屈」は、
① 一 二 三 四 五 六 七 八 九 十 ・ ・ ・ ・ ・
② 上 中 下
だけでなく、
① 一 二 三 四 五 六 七 八 九 十 ・ ・ ・ ・ ・
② 上 中 下
③ 甲 乙 丙 丁 戊 己 庚 辛 壬 癸
④ 天 地 人
⑤ レ
⑥ 一レ 上レ 甲レ 天レ
といふ「返り点」と、
① （ ）
② 〔 〕
③ ［ ］
④ ｛ ｝
といふ「括弧」に対しても、当てはまらざるを得ない。
従って、
（46）（47）により、
（48）
「与えられた順番」が、
① Ｌ＜Ｍ＞Ｎ ＆ Ｌ＝Ｎ＋１
といふ「順番」を含まないのであれば、その時に限って、「返り点・括弧」は、それらの「順番」を、
① １＜２＜３＜４＜５＜６＜７＜８＜９＜１０ ・ ・ ・ ・ ・
といふ「順番（昇べき順）」に「並び替へる（ソートする）」ことが、出来る。
（49）
「返り点、括弧、順列（一昨日の記事）」も、併せてお読み下さい。
（50）
漢語における語順は、国語と大きく違っているところがある。その補足構造における語順は、国語とは全く反対である（鈴木直治著、中国語と漢文、1975年、２９６頁）。
然るに、
（51）
① 我不常読英語。
に於いて、
① 我＝主語
① 常＝修飾語（副詞）
① 英＝修飾語（形容詞）
従って、
（50）（51）により、
（52）
① 我不常読英語＝
① 我不〔常読（英語）〕⇒
② 我〔常（英語）読〕不＝
② 我常には英語を読ま不。
といふ「漢文訓読」が、「可能」となる「所以」は、
① 我不常読英語。
といふ「漢文」には、
① 我不〔常読（英語）〕。
といふ、
①「補足構造」が有って、
② 我常には英語を読ま不。
といふ「和文」には、
② 我〔常（英語）読〕不。
といふ、
②「補足構造」が有るからである。
従って、
（53）
「支那の言語や文字を研究するのに、漢文と支那語の様な区別を設けてゐるのは、世界中、日本だけで、支那はもとより、ヨーロッパやアメリカで支那学を研究するにも、そんな意味のない
区別など夢にも考へてゐない。西洋人が支那のことを研究するには、何よりも先き、支那の現代の言葉を学び、現代人の書く文章を読み、それから次第に順序を追うて、古い言葉で書いた書物を読んで、支那民族の文化の深淵を理解する。アメリカの大学で支那のことを研究する学生は、最初の年に現代語学現代文学を学び、次の年に歴史の書物を読み経書を習ふさうである（勉誠出版、「訓読」論、2008年、５７頁）。さすがに、現在においては、「漢文訓読法」でなければ、日本人だけでなく、中国人も中国古典は理解できない、などという倒錯した主張をなす者はいなくなった。今から考えてみれば「漢文訓読法」派は単に現代中国語ができなかっただけのことではなかったか、そのようにさえ思えてくる（勉誠出版、「訓読」論、2008年、２頁）。
といふこととは、「関係」なく、例へば、
① 我不常読英語＝
① 我不〔常読（英語）〕⇒
② 我〔常（英語）読〕不＝
② 我常には英語を読ま不。
といふ「漢文訓読」に於ける、
① 〔 （ ） 〕
といふ「括弧」は、
① 我不常読英語。
といふ「漢文」の「補足構造（シンタックス）」を、表してゐる。
然るに、
（54）
① 我三〔常二（英一）〕。
に於いて、
① 三＝不
① 二＝読
① 一＝語
とすれば、
① 我三〔常二（英一）〕⇒
② 我〔常（英一）二〕三＝
② 我〔常（英語）読〕不＝
② 我常には英語を読ま不。
従って、
（54）により、
（55）
① 三〔二（一）〕
といふ「返り点・括弧」は、
① 我不〔常読（英語）〕。
といふ「漢文」の「補足構造（シンタックス）」を、表してゐる。
然るに、
（56）
例へば、「新釈漢文大系 全120巻（別巻1） - 明治書院」には、
① 一 二 三 四 五 六 七 八 九 十 ・ ・ ・ ・ ・
② 上 中 下
③ 甲 乙 丙 丁 戊 己 庚 辛 壬 癸
④ 天 地 人
⑤ レ
⑥ 一レ 上レ 甲レ 天レ
が、付けられてゐる。
然るに、
（57）
例へば、
従って、
（58）
例へば、「新釈漢文大系 全120巻（別巻1） - 明治書院」の中に、
① 使籍誠不以畜妻子憂飢寒乱心有銭財以済医薬。
といふ「漢文」が有ったとして、その「返り点」が、
① 人 乙 下 二 一 中 上 甲レ 二 一 地 天
であったなら、その「返り点」を、
① 人 丙 下 二 一 中 上 乙 甲 二 一 地 天
とした上で、次に、
① 人｛丙［下〔二（一）中（上）〕乙（甲）］二（一）地（天）｝
とすれば、
① 人｛丙［下〔二（一）中（上）〕乙（甲）］二（一）地（天）｝
といふ「返り点・括弧」は、
① 使籍誠不以畜妻子憂飢寒乱心有銭財以済医薬。
といふ「漢文」の「補足構造（シンタックス）」を、表してゐる。
従って、
（58）により、
（59）
例へば、「新釈漢文大系 全120巻（別巻1） - 明治書院」には、「返り点」といふ「形」で、「漢文」の「補足構造（シンタックス）」が、示されてゐる。
従って、
（60）
アメリカの大学で支那のことを研究する学生は、最初の年に現代語学現代文学を学び、次の年に歴史の書物を読み経書を習ふさうである（勉誠出版、「訓読」論、2008年、５７頁）。
とのことである、亜米利加の學生が、例へば、
① 使籍誠不以畜妻子憂飢寒乱心有銭財以済医薬。
といふ「漢文」の「補足構造（シンタックス）」を知りたいの場合は、「返り点・括弧」を、知ってゐるべきである。
然るに、
（61）
博士課程後期に六年間在学して訓読が達者になった中国の某君があるとき言った。「自分たちは古典を中国音で音読することができる。しかし、往々にして自ら欺くことがあり、助詞などいいかげんに飛ばして読むことがある。しかし日本式の訓読では、「欲」「将」「当」「謂」などの字が、どこま管到して（かかって）いるか、どの字から上に返って読むか、一字もいいかげんにできず正確に読まなければならない」と、訓読が一字もいやしくしないことに感心していた。これによれば倉石武四郎氏が、訓読は助詞の類を正確に読まないと非難していたが、それは誤りで、訓読こそ中国音で音読するよりも正確な読み方なのである（原田種成、私の漢文 講義、1995年、２７頁）。
従って、
（61）により、
（62）
中國の學生であっても、例へば、
① 使籍誠不以畜妻子憂飢寒乱心有銭財以済医薬。
といふ「漢文」の「補足構造（シンタックス）」を知りたいのであれば、その場合は、「返り点・括弧」を、知ってゐるべきである。
平成２７年１０月２０日、毛利太。
― 「１０月１６日の記事」を、書き換へます。―
（01）
「未」「將」「當」「應」「宜」「須」「猶」「盍」などの諸字は、一字でありながら、最初、副詞に読み、次に動詞あるいは助動詞と読むのが慣例となっている。― 中略 ―
「未」は「いまダ～ず」とよみ、「まだ～しない」の意で、「尚不」と同じである（中沢希男・澁谷玲子、漢文訓読の基礎、1985年、９０頁）。
従って、
（01）により、
（02）
＿未嘗有不可対人言者耳＝
尚不嘗有不可対人言者耳＝
尚不〈嘗有｛不［可〔対（人）言〕］者｝〉耳⇒
尚〈嘗｛［〔（人）対言〕可］不者｝有〉不耳＝
尚だ嘗て人に対して言ふ可から不る者有ら不るのみ。
然るに、
（03）
尚丙〈嘗乙｛下［中〔二（一）上〕］甲｝〉者。
に於いて、
丙＝不
乙＝有
下＝不
中＝可
二＝対
一＝人
上＝言
甲＝者
であれば、
尚丙〈嘗乙｛下［中〔二（一）上〕］甲｝〉者⇒
尚〈嘗｛［〔（一）二上〕中］下甲｝乙〉丙者＝
尚〈嘗｛［〔（人）対言〕可］不者｝有〉不耳＝
尚だ嘗て人に対して言ふ可から不る者有ら不るのみ。
従って、
（02）（03）により、
（04）
尚不嘗有不可対人言者耳＝
尚だ嘗て人に対して言ふ可から不る者有ら不るのみ。
といふ「漢文」に付く「返り点」は、
丙 乙 下 中 二 一 上 甲
である。
然るに、
（05）
従って、
（04）（05）により、
（06）
例へば、
① 下 中 レ 二 レ 一 上
② 二 レ 一レ
③ レ
④ レ レ
⑤ レ レ レ
⑥ 二 一レ 二 一
⑦ 乙 下 二 レ 一レ 上レ レ 甲レ
といふ「返り点（レ点有り）」は、
① 丙 乙 下 中 二 一 上 甲
② 下 二 一 中 上
③ 二 一
④ 三 二 一
⑤ 四 三 二 一
⑥ 四 三 二 一
⑦ 人 丙 下 二 一 中 上 乙 甲 二 一 地 天
といふ「返り点（レ点無し）」に、「置き換へ」ることが、出来る。
従って、
（06）により、
（07）
② 上 中 下
④ 天 地 人
といふ、それぞれの「三組」で「不足」が生じない限り、
① 一 二 三 四 五 六 七 八 九 十 ・ ・ ・ ・ ・
② 上 中 下
③ 甲 乙 丙 丁 戊 己 庚 辛 壬 癸
④ 天 地 人
⑤ レ
⑥ 一レ 上レ 甲レ 天レ
といふ「返り点」で表すことが出来る「順番」の「集合」は、
① 一 二 三 四 五 六 七 八 九 十 ・ ・ ・ ・ ・
② 上 中 下
③ 甲 乙 丙 丁 戊 己 庚 辛 壬 癸
④ 天 地 人
といふ「返り点」で表すことが出来る「順番」の「集合」に、等しい。
従って、
（07）により、
（08）
① （ ）
② 〔 〕
③ ［ ］
④ ｛ ｝
で表すことが出来ない「順番」の「集合」が「集合Β」であるとして、
① 一 二 三 四 五 六 七 八 九 十 ・ ・ ・ ・ ・
② 上 中 下
③ 甲 乙 丙 丁 戊 己 庚 辛 壬 癸
④ 天 地 人
で表すことが出来ない「順番」の「集合」も「集合Β」であるならば、「Βの補集合」は、
① （ ）
② 〔 〕
③ ［ ］
④ ｛ ｝
といふ「括弧」、並びに、
① 一 二 三 四 五 六 七 八 九 十 ・ ・ ・ ・ ・
② 上 中 下
③ 甲 乙 丙 丁 戊 己 庚 辛 壬 癸
④ 天 地 人
⑤ レ
⑥ 一レ 上レ 甲レ 天レ
といふ「返り点」で、表すことが出来る「順番」の『集合』に、等しい。
従って、
（07）（08）により、
（09）
① 一 二 三 四 五 六 七 八 九 十 ・ ・ ・ ・ ・
② 上 中 下
③ 甲 乙 丙 丁 戊 己 庚 辛 壬 癸
④ 天 地 人
⑤ レ
⑥ 一レ 上レ 甲レ 天レ
といふ「返り点」で表すことが出来る「順番」の『集合』は、
① （ ）
② 〔 〕
③ ［ ］
④ ｛ ｝
といふ「括弧」で表すことが出来る「順番」の『集合』に等しい。
といふ「定理」を証明するためには、
① （ ）
② 〔 〕
③ ［ ］
④ ｛ ｝
で表すことが出来ない「順番」の「集合」が、
① 一 二 三 四 五 六 七 八 九 十 ・ ・ ・ ・ ・
② 上 中 下
③ 甲 乙 丙 丁 戊 己 庚 辛 壬 癸
④ 天 地 人
で表すことが出来ない「順番」の「集合」に等しい。
といふことを示せば、「十分」である。
然るに、
（10）
「返り点」とは、「縦書き」であれば、「下から、上へ返る、返り点」であって、それ故、
「返り点」とは、「横書き」であれば、「右から、左へ返る、返り点」であって、それ故、
「返り点」とは、「横書き」であれば、「左から、右へ返る、返り点」ではない。
従って、
（10）により、
（11）
β ： ２←１
α ： ３←２
ε ： ３←２←１
の「順」でなければ、「返り点」は付かない。
従って、
（11）により、
（12）
α ： １ ３ ２
β ： ２ １ ３
γ ： ２ ３ １
δ ： ３ １ ２
ε ： ３ ２ １
であれば、
α ： 囗 ３ ２
β ： ２ １ 囗
γ ： ２ 囗 １
δ ： ３ 囗 ２
ε ： ３ ２ １
とした場合、「返り点」は、「囗の位置」には、付かない。
従って、
（12）により、
（13）
α ： １ ３ ２
β ： ２ １ ３
γ ： ２ ３ １
δ ： ３ １ ２
ε ： ３ ２ １
に付く「一二点」は、
α ： 囗 二 一
β ： 二 一 囗
γ ： 二 囗 一
δ ： 二 囗 一
ε ： 三 二 一
である。
然るに、
（14）
α ： 囗 二 一
β ： 二 一 囗
γ ： 二 囗 一
δ ： 二 囗 一
ε ： 三 二 一
に於いて、「一番最初」に読まれる「囗」を、「＃」に「置き換へ」ると、
α ： ＃ 二 一
β ： 二 一 囗
γ ： 二 ＃ 一
δ ： 二 ＃ 一
ε ： 三 二 一
ｃｆ.
然るに、
（15）
α ： ＃ 二 一
γ ： 二 ＃ 一
δ ： 二 ＃ 一
に於いて、「＃」を、「一番最初」に読むためには、「＃＝〇」として、
α ： 〇 二 一
γ ： 二 〇 一
δ ： 二 〇 一
とする「必要」がある。
然るに、
（16）
α ： 〇 二 一
γ ： 二 〇 一
δ ： 二 〇 一
といふ「順番」は、
α ： 一 三 二
γ ： 三 一 二
δ ： 三 一 二
といふ「順番」、すなはち、
α ： １ ３ ２
γ ： ３ １ ２
δ ： ３ １ ２
に、他ならない。
然るに、
（17）
β ： 二 一 囗
ε ： 三 二 一
の場合は、もちろん、
β ： ２ １ ３
ε ： ３ ２ １
である。
従って、
（16）（17）により、
（18）
α ： １ ３ ２
β ： ２ １ ３
γ ： ３ １ ２
δ ： ３ １ ２
ε ： ３ ２ １
である。
従って、
（13）（18）により、
（19）
γ ： ２ ３ １
であって、
γ ： ３ １ ２
であるものの、
γ ： ２ ３ １
γ ： ３ １ ２
は、もちろん、「矛盾」である。
従って、
（11）～（19）により、
（20）
「返り点」とは、「横書き」であれば、「右から、左へ返る、返り点」であって、
「返り点」とは、「横書き」であれば、「左から、右へ返る、返り点」ではない。
とする限り、
α ： １ ３ ２
β ： ２ １ ３
γ ： ２ ３ １
δ ： ３ １ ２
ε ： ３ ２ １
に於いて、
γ ： ２ ３ １
といふ「順番」に対応する「返り点」は、存在しない。
然るに、
（21）
従って、
（20）（21）により、
（22）
「理屈」の上でも、「事実」の上でも、
γ ： ２ ３ １
といふ「順番」に対応する「返り点」は、存在しない。
然るに、
（23）
α ： １ ３ ２
β ： ２ １ ３
γ ： ２ ３ １
δ ： ３ １ ２
ε ： ３ ２ １
といふ「五つの順番」の内の、
γ ： ２ ３ １
に対して、
① （ ）
② 〔 〕
を加へると、
γ ： ２（３〔１）〕
然るに、
（24）
γ ： ２（３〔１）〕
に於いて、
γ ： ２（ ）⇒（ ）２
γ ： ３〔 〕⇒〔 〕３
とするならば、
γ ： ２（３〔１）〕⇒
γ ： （〔１）２〕３＝１２３。
然るに、
（25）
① （ ）
② 〔 〕
に於いて、
② が有る場合は、② の中には、一つ以上の ① が有って、
① の中には、① が無いならば、その時に限って、「括弧」とする。
然るに、
（26）
γ ： ２（３〔１）〕
の「それ」は、
γ ： （ 〔 ） 〕
であるため、「括弧」ではない。
従って、
（24）（25）（26）により、
（27）
γ ： ２（３〔１）〕⇒
γ ： （〔１）２〕３＝１２３。
といふ「ソート（並び替へ）」は、「括弧」による「ソート（並び替へ）」ではない。
従って、
（27）により、
（28）
α ： １ ３ ２
β ： ２ １ ３
γ ： ２ ３ １
δ ： ３ １ ２
ε ： ３ ２ １
といふ「五つの順番」の内、
γ ： ２ ３ １
に関しては、「括弧」による「ソート（並び替へ）」を行ふことが、出来ない。
然るに、
（25）により、
（29）
α ： １ ３（２）
β ： ２（１ ３）
γ ：
δ ： ３（１ ２）
ε ： ３〔２（１）〕
の場合は、「四つ」とも、「括弧」である。
従って、
（28）（29）により、
（30）
α ： １ ３ ２
β ： ２ １ ３
γ ： ２ ３ １
δ ： ３ １ ２
ε ： ３ ２ １
といふ「五つの順番」の内、
γ ： ２ ３ １
だけは、「括弧」による「ソート（並び替へ）」を行ふことが、出来ない。
従って、
（20）（30）により、
（31）
「3Ｐ3（順列）」、すなはち、
１ ２ ３
１ ３ ２
２ １ ３
２ ３ １
３ １ ２
３ ２ １
といふ「六つの順番」から、
１＜２＜３
を除いた、
α ： １ ３ ２
β ： ２ １ ３
γ ： ２ ３ １
δ ： ３ １ ２
ε ： ３ ２ １
といふ「五つの順番」の内、
γ ： ２ ３ １
だけは、「返り点・括弧」による「ソート（並び替へ）」を行ふことが、出来ない。
従って、
（31）により、
（32）
Ｌ＜Ｍ＞Ｎ ＆ Ｌ＝Ｎ＋１
に於いて、
Ｌ ＝２
Ｍ＝３
Ｎ ＝１
である時、「返り点・括弧」は、
Ｌ＜Ｍ＞Ｎ
を、
Ｎ＜Ｌ＜Ｍ
といふ「順番」に、「並び替へる（ソートする）」ことが出来ない。
（33）
初めから、
１＜２＜３＜４
である、
１ ２ ３ ４
を除いて、
１ ２ ４ ３
１ ３ ２ ４
１ ３ ４ ２
１ ４ ２ ３
１ ４ ３ ２
２ １ ３ ４
２ １ ４ ３
２ ３ １ ４
２ ３ ４ １
２ ４ １ ３
２ ４ ３ １
３ １ ２ ４
３ １ ４ ２
３ ２ １ ４
３ ２ ４ １
３ ４ ２ １
３ ４ １ ２
４ １ ２ ３
４ １ ３ ２
４ ２ １ ３
４ ２ ３ １
４ ３ １ ２
４ ３ ２ １
に対して、「括弧」を加へると、
１ ２ ４（３）
１ ３（２）４
１ ３（４〔２）〕
１ ４（２ ３）
１ ４〔３（２）〕
２（１）３ ４
２（１）４（３）
２（３〔１）〕４
２（３〔４［１）〕］
２（４〔１）３〕
２（４［３〔１）〕］
３（１ ２）４
３（１ ４〔２）〕
３〔２（１）〕４
３〔２（４［１）〕］
３〔４［２（１）〕］
３（４〔１ ２）〕
４（１ ２ ３）
４〔１ ３（２）〕
４〔２（１）３〕
４［２（３〔１）〕］
４〔３（１ ２）〕
４［３〔２（１）〕］
（34）
① （ ）
② 〔 〕
③ ［ ］
に於いて、
③ が有る場合は、③ の中には、一つ以上の ② が有って、
② が有る場合は、② の中には、一つ以上の ① が有って、
① の中には、① が無いならば、その時に限って、「括弧」とする。
従って、
（33）（34）により、
（35）
１ ３（４〔２）〕
２（３〔１）４〕
２（３〔４［１）〕］
２（４〔１）３〕
２（４［３〔１）〕］
３〔１（４［２）〕］
３〔２（４［１）〕］
３〔４［２（１）〕］
３（４〔１ ２）〕
４［２（３〔１）〕］
に於ける、
（ 〔 ）〕
（ 〔 ） 〕
（ 〔 ［ ）〕］
（ 〔 ） 〕
（ ［ 〔 ）〕］
〔 （ ［ ）〕］
〔 （ ［ ）〕］
〔 ［ （ ）〕］
（ 〔 ）〕
［ （ 〔 ）〕］
は、「括弧」ではない。
従って、
（35）により、
（36）
１ ３ ４ ２
２ ３ １ ４
２ ３ ４ １
２ ４ １ ３
２ ４ ３ １
３ １ ４ ２
３ ２ ４ １
３ ４ ２ １
３ ４ １ ２
４ ２ ３ １
といふ「順番」に対しては、
① （ ）
② 〔 〕
③ ［ ］
といふ「括弧」を用ゐた、「ソート（並び替へ）」を行ふことが、出来ない。
然るに、
（37）
例へば、
１ ３ ４ ２
であれば、
１ ３＜４＞２
であるため、
Ｌ ＝３
Ｍ＝４
Ｎ ＝２
である時、
１ ３ ４ ２
といふ「順番」は、
Ｌ＜Ｍ＞Ｎ ＆ Ｌ＝Ｎ＋１
といふ「順番」を、含んでゐる。
（38）
例へば、
３ １ ４ ２
であれば、
３＞１＜４＞２
であるため、
Ｌ ＝３
Ｍ＝４
Ｎ ＝２
である時、
３ １ ４ ２
といふ「順番」は、
Ｌ＜Ｍ＞Ｎ ＆ Ｌ＝Ｎ＋１
といふ「順番」を、含んでゐる。
従って、
（37）（38）により、
（39）
１ ３ ４ ２
２ ３ １ ４
２ ３ ４ １
２ ４ １ ３
２ ４ ３ １
３ １ ４ ２
３ ２ ４ １
３ ４ ２ １
３ ４ １ ２
４ ２ ３ １
といふ「順番」は、
１＜３＜４＞２
２＜３＞１＜４
２＜３＜４＞１
２＜４＞１＜３
２＜４＞３＞１
３＞１＜４＞２
３＞２＜４＞１
３＜４＞２＞１
３＜４＞１＜２
４＞２＜３＞１
であるが故に、「１０個」とも、
Ｌ＜Ｍ＞Ｎ ＆ Ｌ＝Ｎ＋１
といふ「順番」を、含んでゐる。
然るに、
（40）
１ ２ ４ ３
１ ３ ２ ４
１ ４ ２ ３
１ ４ ３ ２
２ １ ３ ４
２ １ ４ ３
３ １ ２ ４
３ ２ １ ４
４ １ ２ ３
４ １ ３ ２
４ ２ １ ３
４ ３ １ ２
４ ３ ２ １
の場合は、
１＜２＜４＞３
１＜３＞２＜４
１＜４＞２＜３
１＞４＞３＜２
２＞１＜３＜４
２＞１＜４＞３
３＞１＜２＜４
３＞２＞１＜４
４＞１＜２＜３
４＞１＜３＞２
４＞２＞１＜３
４＞３＞１＜２
４＞３＞２＞１
であるため、「１３個」とも、
Ｌ＜Ｍ＞Ｎ ＆ Ｌ＝Ｎ＋１
といふ「順番」を含んでゐない。
従って、
（33）～（40）により、
（41）
「順列（4Ｐ4）」から、
１＜２＜３＜４
を除いた「順番」を、
１ ２ ４ ３
１ ３ ２ ４
１ ４ ２ ３
１ ４ ３ ２
２ １ ３ ４
２ １ ４ ３
３ １ ２ ４
３ ２ １ ４
４ １ ２ ３
４ １ ３ ２
４ ２ １ ３
４ ３ １ ２
４ ３ ２ １
といふ「集合Α」と、
１ ３ ４ ２
２ ３ １ ４
２ ３ ４ １
２ ４ １ ３
２ ４ ３ １
３ １ ４ ２
３ ２ ４ １
３ ４ ２ １
３ ４ １ ２
４ ２ ３ １
といふ「集合Β」に、分けた場合、
①「集合Α」は、「括弧」を用ゐた、「ソート（並び替へ）」を行ふことが、出来、尚且つ、
①「集合Α」は、「Ｌ＜Ｍ＞Ｎ ＆ Ｌ＝Ｎ＋１」といふ「順番」を含んでゐない。
②「集合Β」は、「括弧」を用ゐた、「ソート（並び替へ）」を行ふことが、出来ずに、尚且つ、
②「集合Β」は、「Ｌ＜Ｍ＞Ｎ ＆ Ｌ＝Ｎ＋１」といふ「順番」を含んでゐる。
従って、
（41）により、
（42）
「順列（4Ｐ4）」から、
１＜２＜３＜４
を除いた場合、「与えられた順番」が、「Ｌ＜Ｍ＞Ｎ ＆ Ｌ＝Ｎ＋１」といふ「順番」を含んでゐないならば、その時に限って、その「順番」は、「括弧」を用ゐた「ソート（並び替
へ）」が、可能である。
然るに、
（43）
「集合Α」の「返り点」は、
１ ３ ４ ２ ： 二 三 一
２ ３ １ ４ ： 二 三 一
２ ３ ４ １ ： 二 三 四 一
２ ４ １ ３ ： 二 四 一 三
２ ４ ３ １ ： 二 三レ 一
３ １ ４ ２ ： 二 三 一
３ ２ ４ １ ： 三 二 四 一
３ ４ ２ １ ： 二 三 一レ
３ ４ １ ２ ： 二 三 一
４ ２ ３ １ ： 四 二 三 一
である。
（44）
「集合Β」の「それ」は、
１ ３ ４ ２ ： 二 三 一
２ ３ １ ４ ： 二 三 一
２ ３ ４ １ ： 二 三 四 一
２ ４ １ ３ ： 二 四 一 三
２ ４ ３ １ ： 二 三レ 一
３ １ ４ ２ ： 二 三 一
３ ２ ４ １ ： 三 二 四 一
３ ４ ２ １ ： 二 三 一レ
３ ４ １ ２ ： 二 三 一
４ ２ ３ １ ： 四 二 三 一
である。
然るに、
（45）
「返り点」は、「横書き」であれば、「左へ返る点」であって、「右へ返る点」ではない。が故に、
１ ２ ４ ３ ： レ
１ ３ ２ ４ ： レ
１ ４ ２ ３ ： 二 一
１ ４ ３ ２ ： レ レ
２ １ ３ ４ ： レ
２ １ ４ ３ ： レ レ
３ １ ２ ４ ： 二 一
３ ２ １ ４ ： レ レ
４ １ ２ ３ ： 二 一
４ １ ３ ２ ： 二 一レ
４ ２ １ ３ ： 二 レ 一
４ ３ １ ２ ： レ 二 一
４ ３ ２ １ ： レ レ レ
の「それ」は、「返り点」である。一方で、
１ ３ ４ ２ ： 二 三 一
２ ３ １ ４ ： 二 三 一
２ ３ ４ １ ： 二 三 四 一
２ ４ １ ３ ： 二 四 一 三
２ ４ ３ １ ： 二 三レ 一
３ １ ４ ２ ： 二 三 一
３ ２ ４ １ ： 三 二 四 一
３ ４ ２ １ ： 二 三 一レ
３ ４ １ ２ ： 二 三 一
４ ２ ３ １ ： 四 二 三 一
の「それ」は、「返り点」ではない。
従って、
（41）～（45）により、
（46）
「順列（4Ｐ4）」から、
１＜２＜３＜４
を除いた場合、「与えられた順番」が、「Ｌ＜Ｍ＞Ｎ ＆ Ｌ＝Ｎ＋１」といふ「順番」を含んでゐないならば、その時に限って、その「順番」は、「返り点・括弧」を用ゐた「ソート
（並び替へ）」が、可能である。
従って、
（31）（32）（46）により、
（47）
１＜２＜３
１ ３ ２
２ １ ３
２ ３ １
３ １ ２
３ ２ １
１＜２＜３＜４
１ ２ ４ ３
１ ３ ２ ４
１ ３ ４ ２
１ ４ ２ ３
１ ４ ３ ２
２ １ ３ ４
２ １ ４ ３
２ ３ １ ４
２ ３ ４ １
２ ４ １ ３
２ ４ ３ １
３ １ ２ ４
３ １ ４ ２
３ ２ １ ４
３ ２ ４ １
３ ４ ２ １
３ ４ １ ２
４ １ ２ ３
４ １ ３ ２
４ ２ １ ３
４ ２ ３ １
４ ３ １ ２
４ ３ ２ １
から、
１＜２＜３
１＜２＜３＜４
を除ゐた場合、
Ｌ＜Ｍ＞Ｎ ＆ Ｌ＝Ｎ＋１
Ｌ＜Ｍ＞Ｎ
を含む「順番」を含まないならば、その時に限って、「返り点・括弧」による、「並び替へ（ソート）」が、可能になる。
従って、
（47）により、
（48）
２ ３ １
２ ３ ４ １
のやうな「順番」の場合は、「括弧」を用ゐた、「ソート（並び替へ）」を行ふことが、出来ない。
然るに、
（49）
２ ３ １
２ ３ ４ １
に於いて、さうであれば、
３ ４ ２
３ ４ ５ ２
に於いても、さうであり、それ故、
１ ３ ４ ２
１ ３ ４ ５ ２
のやうな「順番」の場合も、「括弧」を用ゐた、「ソート（並び替へ）」を行ふことが、出来ない。
然るに、
（50）
１ ３ ４ ２
１ ３ ４ ５ ２
に於いて、さうであれば、
１１ １３ １４ １２
１１ １３ １４ １５ １２
のやうな「順番」の場合も、「括弧」を用ゐた、「ソート（並び替へ）」を行ふことが、出来ない。
従って、
（25）（34）（48）（49）（50）により、
（51）
① （ ）
② 〔 〕
③ ［ ］
④ ｛ ｝
に於いて、
④ が有る場合は、④ の中には、一つ以上の ③ が有って、
③ が有る場合は、③ の中には、一つ以上の ② が有って、
② が有る場合は、② の中には、一つ以上の ① が有って、
① の中には、① が無いならば、その時に限って、「括弧」である。
とするとき、
Ｌ＜Ｍ＞Ｍ ＆ Ｌ＝Ｎ＋１
といふ「順番」を含む「順番」であれば、その時に限って、「括弧」を用ゐた、「ソート（並び替へ）」を行ふことは、出来ない。
然るに、
（52）
２０ １ ２ １２ ９ ５ ３ ４ ８ ６ ７ １１ １０ １５ １３ １４ １６ １９ １７ １８＝
２０｛１ ２ １２［９〔５（３ ４）８（６ ７）〕１１（１０）］１５（１３ １４）１６ １９（１７ １８）｝⇒
｛１ ２ ［〔（３ ４）５（６ ７）８〕９（１０）１１］１２（１３ １４）１５１６ （１７ １８）１９｝２０＝
１ ２ ３ ４ ５ ６ ７ ８ ９ １０ １１ １２ １３ １４ １５ １６ １７ １８ １９ ２０
従って、
（51）（52）により、
（53）
２０＞１＜２＜１２＞９＞５＞３＜４＜８＞６＜７＜１１＞１０＜１５＞１３＜１４＜１６＜１９＞１７＜１８
といふ「順番」は、
Ｌ＜Ｍ＞Ｍ ＆ Ｌ＝Ｎ＋１
といふ「順番」を含まない。
然るに、
（54）
２０｛１ ２ １２［９〔５（３ ４）８（６ ７）〕１１（１０）］１５（１３ １４）１６ １９（１７ １８）｝
に於いて、
１ ２ ３ ６ １３ １６ １７
の場合は、「そのまま、上から下（左から右）へ読む」ため、「返り点」は、固より、「不要」である。
従って、
（54）により、
（55）
「返り点」を考へる場合に、「１ ２ ３ ６ １３ １６ １７」は「不要」であるため、
２０｛１ ２ １２［９〔５（３ ４）８（６ ７）〕１１（１０）］１５（１３ １４）１６ １９（１７ １８）｝⇒
２０｛１２［９〔５（４）８（７）〕１１（１０）］１５（１４）１９（１８）｝⇒
１３｛８［５〔２（１）４（３）〕７（６）］１０（９）１２（１１）｝。
とすれば、
１３ ８ ５ ２ １ ４ ３ ７ ６ １０ ９ １２ １１
といふ「順番」は、「返り点」に、相当する。
然るに、
（56）
２０ １ ２ １２ ９ ５ ３ ４ ８ ６ ７ １１ １０ １５ １３ １４ １６ １９ １７ １８
といふ「順番」に対して、
十三 八 五 二 一 四 三 七 六 十 九 十二 十一
といふ「一二点」だけを加へるならば、
使＝20＝十三
籍＝１
誠＝２
不＝12＝八
以＝９ ＝五
畜＝５ ＝二
妻＝３
子＝４ ＝一
憂＝８ ＝四
飢＝６
寒＝７ ＝三
乱＝11＝七
心＝10＝六
有＝15＝十
銭＝13
財＝14＝九
以＝16
済＝19＝十二
医＝17
薬＝18＝十一
然るに、
（57）
一・二点をはさんで返る時は上・中・下点。
上・中・下点をはさんで返る時は甲・乙点。
甲・乙点をはさんで返る時は天・地（天・地・人）点である。
（志村和久、漢文早わかり、1982年、２０頁）
従って、
（56）（57）により、
（58）
使＝20＝人
籍＝１
誠＝２
不＝12＝丙
以＝９ ＝下
畜＝５ ＝二
妻＝３
子＝４ ＝一
憂＝８ ＝中
飢＝６
寒＝７ ＝上
乱＝11＝乙
心＝10＝甲
有＝15＝二
銭＝13
財＝14＝一
以＝16
済＝19＝地
医＝17
薬＝18＝天
ｃｆ.
従って、
（52）～（58）により、
（59）
① 使籍誠不以畜妻子憂飢寒乱心有銭財以済医薬＝
① 使｛籍誠不［以〔畜（妻子）憂（飢寒）〕乱（心）］有（銭財）以済（医薬）｝⇒
①｛籍誠［〔（妻子）畜（飢寒）憂〕以（心）乱］不（銭財）有以（医薬）済｝使＝
①｛籍をして誠に［〔（妻子を）畜ひ（飢寒を）憂ふるを〕以て（心を）乱さ］不（銭財）有りて以て（医薬を）済さ｝使む。
に付く「返り点」は、
① 人 丙 下 二 一 中 上 乙 甲 二 一 地 天
である。
然るに、
（60）
使＝20＝人
籍＝１
誠＝２
不＝12＝丙
以＝９ ＝下
畜＝５ ＝二
妻＝３
子＝４ ＝一
憂＝８ ＝中
飢＝６
寒＝７ ＝上
乱＝11＝乙
心＝10＝甲
有＝15＝二
銭＝13
財＝14＝一
以＝16
済＝19＝地
医＝17
薬＝18＝天
に於いて、
使＝20＝人
が
不＝12＝丙
と、
以＝９＝下
の間に移動した場合が、（61）である。
（61）
籍＝１
誠＝２
不＝12＝丙
使＝20＝人
以＝９ ＝下
畜＝５ ＝二
妻＝３
子＝４ ＝一
憂＝８ ＝中
飢＝６
寒＝７ ＝上
乱＝11＝乙
心＝10＝甲
有＝15＝二
銭＝13
財＝14＝一
以＝16
済＝19＝地
医＝17
薬＝18＝天
然るに、
（51）（57）（61）により、
（62）
丙 人 乙
であれば、
甲・乙点が、天・地点をはさんでゐる。
が故に、「返り点」として、「矛盾」するし、
１２＜２０＞１１
であるため、すなはち、
Ｌ＜Ｍ＞Ｍ ＆ Ｌ＝Ｎ＋１
であるため、「括弧」は無い。
（63）
使＝20＝人
籍＝１
誠＝２
不＝12＝丙
以＝９ ＝下
畜＝５ ＝二
妻＝３
子＝４ ＝一
憂＝８ ＝中
飢＝６
寒＝７ ＝上
乱＝11＝乙
心＝10＝甲
有＝15＝二
銭＝13
財＝14＝一
以＝16
済＝19＝地
医＝17
薬＝18＝天
に於いて、
心＝10＝甲
が
畜＝５＝二
と、
子＝４＝一
の間に移動した場合が、（64）である
（64）
使＝20＝人
籍＝１
誠＝２
不＝12＝丙
以＝９ ＝下
畜＝５ ＝二
妻＝３
心＝10＝甲
子＝４ ＝一
憂＝８ ＝中
飢＝６
寒＝７ ＝上
乱＝11＝乙
有＝15＝二
銭＝13
財＝14＝一
以＝16
済＝19＝地
医＝17
薬＝18＝天
然るに、
（51）（57）（64）により、
（65）
二 甲 一
であれば、
一・二点が、甲・乙点をはさんでゐる。
が故に、「矛盾」するし、
５＜１０＞４
であるため、すなはち、
Ｌ＜Ｍ＞Ｍ ＆ Ｌ＝Ｎ＋１
であるため、「括弧」は無い。
（66）
使＝20＝人
籍＝１
誠＝２
不＝12＝丙
以＝９ ＝下
畜＝５ ＝二
妻＝３
子＝４ ＝一
憂＝８ ＝中
飢＝６
寒＝７ ＝上
乱＝11＝乙
心＝10＝甲
有＝15＝二
銭＝13
財＝14＝一
以＝16
済＝19＝地
医＝17
薬＝18＝天
に於いて、
心＝10＝甲
が
有＝15＝二
と、
財＝14＝一
の間に移動した場合が、（67）である。
（67）
使＝20＝人
籍＝１
誠＝２
不＝12＝丙
以＝９ ＝下
畜＝５ ＝二
妻＝３
子＝４ ＝一
憂＝８ ＝中
飢＝６
寒＝７ ＝上
乱＝11＝乙
有＝15＝二
銭＝13
心＝10＝甲
財＝14＝一
以＝16
済＝19＝地
医＝17
薬＝18＝天
然るに、
（51）（57）（67）により、
（68）
乙 二 甲 一
であれば、
一・二点が、甲・乙点をはさんでゐる。
が故に、「矛盾」するし、
１１＜１５＞１０＞１４
であるため、すなはち、
Ｌ＜Ｍ＞Ｍ ＆ Ｌ＝Ｎ＋１
であるため、「括弧」は無い。
（69）
使＝20＝人
籍＝１
誠＝２
不＝12＝丙
以＝９ ＝下
畜＝５ ＝二
妻＝３
子＝４ ＝一
憂＝８ ＝中
飢＝６
寒＝７ ＝上
乱＝11＝乙
心＝10＝甲
有＝15＝二
銭＝13
財＝14＝一
以＝16
済＝19＝地
医＝17
薬＝18＝天
に於いて、
不＝12＝丙
が
有＝15＝二
と、
銭＝13
財＝14＝一
の間に移動した場合が、（70）である。
（70）
使＝20＝人
籍＝１
誠＝２
以＝９ ＝下
畜＝５ ＝二
妻＝３
子＝４ ＝一
憂＝８ ＝中
飢＝６
寒＝７ ＝上
乱＝11＝乙
心＝10＝甲
有＝15＝二
不＝12＝丙
銭＝13
財＝14＝一
以＝16
済＝19＝地
医＝17
薬＝18＝天
然るに、
（57）により、
（58）
不＝12＝丙
銭＝13
であれば、
有＝15＝二
不＝12
銭＝13
財＝14＝一
となって、「丙」は、消えてしまふ。
（71）
２０｛１ ２ １２［９〔５（３ ４）８（６ ７）〕１１（１０）］１５（１３ １４）１６ １９（１７ １８）｝
に対して、
２０〈１ ２ １９｛１２［９〔５（３ ４）８（６ ７）〕１１（１０）］１５（１３ １４）１６ １７ １８｝〉
であるため、
（ ）
〔 〕
［ ］
｛ ｝
に対して、
〈 〉を加へれば、「返り点・括弧」は、
使＝20＝人
籍＝１
誠＝２
済＝19＝地
不＝12＝丙
以＝９ ＝下
畜＝５ ＝二
妻＝３
子＝４ ＝一
憂＝８ ＝中
飢＝６
寒＝７ ＝上
乱＝11＝乙
心＝10＝甲
有＝15＝二
銭＝13
財＝14＝一
以＝16
医＝17
薬＝18＝天
といふ「順番」を表すことが、出来る。
（72）
２０｛１ ２ １２［９〔５（３ ４）８（６ ７）〕１１（１０）］１５（１３ １４）１９〔１７（１６）１８〕｝
であるため、「返り点・括弧」は、
使＝20＝人
籍＝１
誠＝２
不＝12＝丙
以＝９ ＝下
畜＝５ ＝二
妻＝３
子＝４ ＝一
憂＝８ ＝中
飢＝６
寒＝７ ＝上
乱＝11＝乙
心＝10＝甲
有＝15＝二
銭＝13
財＝14＝一
済＝19＝地
医＝17＝二
以＝16＝一
薬＝18＝天
といふ「順番」を表すことが、出来る。
（73）
使＝20＝人
籍＝１
誠＝２
不＝12＝丙
以＝９ ＝下
畜＝５ ＝二
妻＝３
子＝４ ＝一
憂＝８ ＝中
飢＝６
寒＝７ ＝上
乱＝11＝乙
心＝10＝甲
有＝15＝二
銭＝13
財＝14＝一
以＝16
済＝19＝地
医＝17
薬＝18＝天
に於いて、
済＝19＝地
が
有＝15＝二
と、
銭＝13
財＝14＝一
の間に移動した場合が、（74）である。
（74）
使＝20＝人
籍＝１
誠＝２
不＝12＝丙
以＝９ ＝下
畜＝５ ＝二
妻＝３
子＝４ ＝一
憂＝８ ＝中
飢＝６
寒＝７ ＝上
乱＝11＝乙
心＝10＝甲
有＝15＝二
済＝19＝地
銭＝13
財＝14＝一
以＝16
医＝17
薬＝18＝天
然るに、
（51）（57）（74）により、
（75）
二 地 一
であれば、
一・二点が、天・地点をはさんでゐる。
が故に、「矛盾」するし、
１５＜１９＞１３・１４
であるため、すなはち、
Ｌ＜Ｍ＞Ｍ ＆ Ｌ＝Ｎ＋１
であるため、「括弧」は無い。といふ「意味」は、
２０｛１ ２ １２［９〔５（３ ４）８（６ ７）〕１１（１０）］１５（１９〔１３ １４）１６ １７ １８〕｝⇒
｛１ ２ ［９〔（３ ４）５（６ ７）８〕（１０）１１］１２（〔１３ １４）１５１６ １７ １８〕１９｝２０。
に於ける、
１５（１９〔１３ １４）１６ １７ １８〕
といふ「部分」の、
（ 〔 ） 〕
といふ「それ」が、「括弧」ではない。といふことに、他ならない。
（76）
使＝20＝人
籍＝１
誠＝２
不＝12＝丙
以＝９ ＝下
畜＝５ ＝二
妻＝３
子＝４ ＝一
憂＝８ ＝中
飢＝６
寒＝７ ＝上
乱＝11＝乙
心＝10＝甲
有＝15＝二
銭＝13
財＝14＝一
以＝16
済＝19＝地
医＝17
薬＝18＝天
に於いて、
薬＝18＝天
が
有＝15＝二
と、
銭＝13
財＝14＝一
の間に移動した場合が、（77）である。
（77）
使＝20＝人
籍＝１
誠＝２
不＝12＝丙
以＝９ ＝下
畜＝５ ＝二
妻＝３
子＝４ ＝一
憂＝８ ＝中
飢＝６
寒＝７ ＝上
乱＝11＝乙
心＝10＝甲
有＝15＝二
薬＝18＝天
銭＝13
財＝14＝一
以＝16
済＝19＝地
医＝17
然るに、
（51）（57）（77）により、
（78）
二 天 一
であれば、
一・二点が、天・地点をはさんでゐる。
が故に、「矛盾」するし、
１５＜１８＞１３・１４
であるため、すなはち、
Ｌ＜Ｍ＞Ｍ ＆ Ｌ＝Ｎ＋１
であるため、「括弧」は無い。といふ「意味」は、
２０｛１ ２ １２［９〔５（３ ４）８（６ ７）〕１１（１０）］１５（１８〔１３ １４）１６ １９［１７〕］｝⇒
｛１ ２ １２［９〔５（３ ４）８（６ ７）〕１１（１０）］（〔１３ １４）１５１６ ［１７〕１８］１９｝２０。
に於ける、
１５（１８〔１３ １４）１６ １９［１７〕］
といふの「部分」の
（ 〔 ）［ 〕 ］
といふ「それ」が、「括弧」ではない。といふことに、他ならない。
然るに、
（79）
使＝20＝囗
籍＝１
誠＝２
不＝12＝丙
以＝９ ＝下
畜＝５ ＝二
妻＝３
子＝４ ＝一
憂＝８ ＝中
飢＝６
寒＝７ ＝上
乱＝11＝乙
心＝10＝甲
済＝19＝人
有＝15＝二
銭＝13
財＝14＝一
以＝16
薬＝18＝地
医＝17＝天
であれば、
２０｛１ ２ １２［９〔５（３ ４）８（６ ７）〕１１（１０）］１９〔１５（１３ １４）１６１８（１７）〕｝⇒
｛１ ２ ［〔（３ ４）５（６ ７）８〕９（１０）１１］１２〔（１３ １４）１５１６（１７）１８〕１９｝２０。
であるため、
① （ ）
② 〔 〕
③ ［ ］
④ ｛ ｝
については、「不足」しないものの、、
① 一 二 三 四 五 六 七 八 九 十 ・ ・ ・ ・ ・
② 上 中 下
③ 甲 乙 丙 丁 戊 己 庚 辛 壬 癸
④ 天 地 人 囗
に於ける、
④ 囗 が、「不足」する。
従って、
（01）～（79）により、
（80）
① 一 二 三 四 五 六 七 八 九 十 ・ ・ ・ ・ ・
② 上 中 下
③ 甲 乙 丙 丁 戊 己 庚 辛 壬 癸
④ 天 地 人
といふ「返り点」で表すことが出来る「順番」の「集合」、すなはち、
① 一 二 三 四 五 六 七 八 九 十 ・ ・ ・ ・ ・
② 上 中 下
③ 甲 乙 丙 丁 戊 己 庚 辛 壬 癸
④ 天 地 人
⑤ レ
⑥ 一レ 上レ 甲レ 天レ
といふ「返り点」で表すことが出来る「順番」の「集合」と、
① （ ）
② 〔 〕
③ ［ ］
④ ｛ ｝
で表すことが出来る「順番」の「集合」は、
② 上 中 下
④ 天 地 人
の、それぞれの「三つ」が「不足」しない限り、
④ ｛ ｝
の次の、
⑤ 〈 〉
を「必要」としない限り、等しい。
要するに、
（81）
「返り点」は、「縦書き」であれば、「上へ返る点」であって、「下へ返る点」ではない。が故に、
「返り点」は、「横書き」であれば、「左へ返る点」であって、「右へ返る点」ではない。にも拘はらず、
Ｌ＜Ｍ＞Ｍ ＆ Ｌ＝Ｎ＋１
といふ「順番」を、「返り点」を用ゐて、
Ｎ＜Ｌ＜Ｍ
といふ「順番」に「ソートし（並び替へ）」ようとすると、「下へ返る、返る点」を、用ゐざるを得ず、それ故、「（返り点としての）反則」が生じ、その際に、「括弧」であれば、
二（三〔一）〕に於ける、（ 〔 ） 〕のやうな、「（括弧としての）反則」が、生じることになる。
従って、
（82）
① 一 二 三 四 五 六 七 八 九 十 ・ ・ ・ ・ ・
② 上 中 下
③ 甲 乙 丙 丁 戊 己 庚 辛 壬 癸
④ 天 地 人
⑤ レ
⑥ 一レ 上レ 甲レ 天レ
といふ「返り点」を、「下へ返る点」として、用ゐることが無いのであれば、その時に限って、
① （ ）
② 〔 〕
③ ［ ］
④ ｛ ｝
といふ「括弧」が、表すことが出来る「順番」の「集合」と、
① 一 二 三 四 五 六 七 八 九 十 ・ ・ ・ ・ ・
② 上 中 下
③ 甲 乙 丙 丁 戊 己 庚 辛 壬 癸
④ 天 地 人
⑤ レ
⑥ 一レ 上レ 甲レ 天レ
といふ「返り点」が、表すことが出来る「順番」の「集合」は、等しい。
Ｑ.Ｅ.Ｄ.
平成２７年１０月１７日、毛利太。
― 「熟語の場合」―
（83）
① 読（漢文）⇒
① （漢文）読＝
① （漢文を）読む。
に対して、
② 訓‐読（漢文）⇒
② （漢文）訓‐読＝
② （漢文を）訓‐読す。
従って、
（84）
① ３（１ ２）⇒
① （１ ２）３。
に対して、
② ３‐４（１ ２）⇒
② （１ ２）３‐４。
然るに、
（85）
② ３‐４ １ ２
に於いて、
② Ｌ ＝３
② Ｍ＝４
② Ｎ ＝２
であれば、
② Ｌ＜Ｍ＞Ｎ ＆ Ｌ＝Ｎ＋１
である。
然るに、
（86）
②「訓読」のやうな、「二字熟語」は、
②「一語」と、見なす。
従って、
（87）
② 訓‐読（漢文）⇒
② （漢文）訓‐読＝
② （漢文を）訓‐読す。
の場合も、
① 読（漢文）⇒
① （漢文）読＝
① （漢文を）読む。
と同様に、
② ３（１ ２）⇒
② （１ ２）３。
であって、
② ３‐４（１ ２）⇒
② （１ ２）３‐４。
ではない。
ｃｆ.
従って、
（88）
② 訓‐読（漢文）。
の場合も、
② Ｌ＜Ｍ＞Ｎ ＆ Ｌ＝Ｎ＋１
ではない。
（89）
③ 先‐後‐生（三文字）
等も、「一語」と見なすため、
③ ３‐４‐５（１ ２）⇒
③ （１ ２）３‐４‐５。
とは、ならず、それ故、
③ Ｌ＜Ｍ＞Ｎ ＆ Ｌ＝Ｎ＋１
ではない。
― 「白話（中国語）」の場合 ―
（90）
例へば、「新釈漢文大系 全120巻（別巻1） - 明治書院」には、
① 一 二 三 四 五 六 七 八 九 十 ・ ・ ・ ・ ・
② 上 中 下
③ 甲 乙 丙 丁 戊 己 庚 辛 壬 癸
④ 天 地 人
⑤ レ
⑥ 一レ 上レ 甲レ 天レ
が、付けられてゐる。
従って、
（82）（90）により、
（91）
「新釈漢文大系 全120巻（別巻1） - 明治書院」に対しては、
① （ ）
② 〔 〕
③ ［ ］
④ ｛ ｝
⑤ 〈 〉
を、付けることが、出来る。
然るに、
（92）
然るに、
（93）
α ： ４ ２＜３＞１ （下 二 上 一）
β ： ２＜５ ３＞１ ４（二 五 三 一 四）
γ ： ２＜４ ３＞１ （二 三レ 一）
であるため、「括弧」を付けることが、出来ないし、
（94）
α ： 下 二 上 一
β ： 二 五 三 一 四
γ ： 二 三レ 一
の場合は、「上から下へ、返ってゐる」ため、「返り点」ではない。
従って、
（91）～（94）により、
（95）
「白話文（中国語）訓読」に於ける、
α ： 只管要纏擾我（下 二 上 一）。
β ： 端的看不出這婆子的本事来 （二 五 三 一 四）。
β ： 西門慶促忙促急儧造不出床来（二 五 三 一 四）。
γ ： 吃了不多酒（二 三レ 一）。
といふ「語順」は、「漢文訓読」から見ると、「異常」である。
従って、
（96）
「漢文」と「白話文（中国語）」は、甚だ、著しく、完全に、「異なる言語」であるとしか、思へない。
それ故、
（97）
私は中国語の勉強をお勧めします。私も中国語を勉強して白文を読むのが楽になりました（kiebine2007さん）。
といふことが、私には、信じられない。
平成２７年１０月１９日、毛利太。
