分配の法則（の、命題計算と真理値表）。

（01）
（ⅰ）
１　　（１）　Ｐ＆（Ｑ∨Ｒ）　　　　Ａ
１　　（２）　Ｐ　　　　　　　　　　１＆Ｅ
１　　（３）　　　（Ｑ∨Ｒ）　　　　１＆Ｅ
　４　（４）　　　　Ｑ　　　　　　　Ａ
１４　（５）　Ｐ＆Ｑ　　　　　　　　２３＆Ｉ
１４　（６）（Ｐ＆Ｑ）∨（Ｐ＆Ｒ）　５∨Ｉ
　　７（７）　　　　　　Ｒ　　　　　Ａ
１　７（８）　　　　　　　Ｐ＆Ｒ　　２７＆Ｉ
１　７（９）（Ｐ＆Ｑ）∨（Ｐ＆Ｒ）　８∨Ｉ
１　　（ア）（Ｐ＆Ｑ）∨（Ｐ＆Ｒ）　３４６７９∨Ｅ
（ⅱ）
１　　（１）（Ｐ＆Ｑ）∨（Ｐ＆Ｒ）　Ａ
　２　（２）　Ｐ＆Ｑ　　　　　　　　Ａ
　２　（３）　Ｐ　　　　　　　　　　２＆Ｅ
　２　（４）　　　Ｑ　　　　　　　　２＆Ｅ
　２　（５）　　　Ｑ∨Ｒ　　　　　　４∨Ｉ
　２　（６）Ｐ＆（Ｑ∨Ｒ）　　　　　３５＆Ｉ
　　７（７）　　　　　　　Ｐ＆Ｒ　　Ａ
　　７（８）　　　　　　　Ｐ　　　　７＆Ｅ
　　７（９）　　　　　　　　　Ｒ　　７＆Ｅ
　　７（ア）　　　　　　　Ｑ∨Ｒ　　９∨Ｉ
　　７（イ）　　　　Ｐ＆（Ｑ∨Ｒ）　８ア＆Ｉ
１　　（ウ）Ｐ＆（Ｑ∨Ｒ）　　　　　１２７６イ∨Ｅ
といふ「命題計算（propositional calculus）」は、概ね、
（ⅰ）
（１）「Ｐであって、その上（Ｑであるか、または、Ｒである）。」従って、
（２）「いづれにせよ、Ｐである。」従って、（１）（２）により、
（３）「ＰであってＱであるか、または、ＰであってＱである。」
（ⅱ）
（１）「ＰであってＱであるか、または、ＰであってＱである。」従って、
（２）「いづれにせよ、Ｐである。」従って、（１）（２）により、
（３）「Ｐであって、その上（Ｑであるか、または、Ｒである）。」
といふ「意味」である。
従って、
（01）により、
（02）
① Ｐ＆（Ｑ∨Ｒ）
②（Ｐ＆Ｑ）∨（Ｐ＆Ｒ）
に於いて、すなはち、
① Ｐであって、その上（Ｑであるか、または、Ｒである）。
② ＰであってＱであるか、または、ＰであってＲである。
に於いて、
①＝② である（分配法則）。
従って、
（01）（02）により、
（03）
（ａ）「命題計算（propositional calculus）」は、
（ｂ）「自然言語（natural language）」に似てゐる。
然るに、
（04）

従って、
（04）により、
（05）
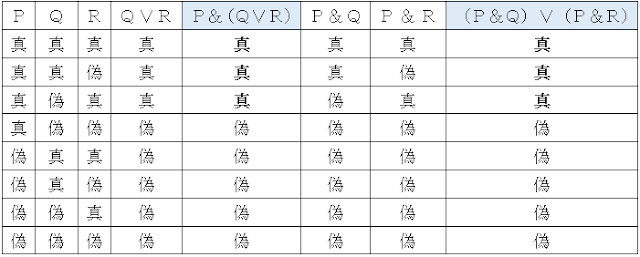
「真理値表（Truth table）」により、
① Ｐ＆（Ｑ∨Ｒ）
②（Ｐ＆Ｑ）∨（Ｐ＆Ｒ）
に於いて、
① の「真理値」と、
② の「真理値」は、「等しく」、それ故、
①＝② である。
然るに、
（06）
（ａ）「命題計算（propositional calculus）」と、
（ｂ）「自然言語（natural language）」と、
（ｃ）「真理値表（Truth table）」と
比較すると、
（ａ）と（ｂ）が「似てゐる」のに対して、
（ａ）と（ｃ）は「似てゐない」。
（01）～（06）により、
（07）
（ａ）「命題計算」による「証明」は、「自然言語的」であるが、
（ｂ）「真理値表」による「証明」は、「自然言語的」ではない。
令和０３年０２月０２日、毛利太。