「ある（明らかな）医療過誤」について。

　　　　　　　　　―「興味」が無い方には、迷惑かも知れないものの、改めて、以下の内容を記すことにします。―
（01）
「議論」を進めるためには、「公理（共通の認識）」が「必要」があるため、以下の「３条件」を「公理」とします。

（出典: フリー百科事典『ウィキペディア（Wikipedia）』）

然るに、
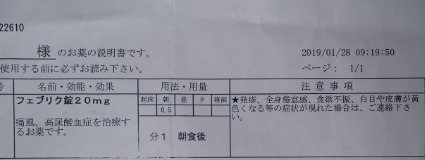
（02）

痛風発作再発予防が必要であると考え２０１９年０１月０５日からフェブリク錠投与を開始したものです。
（２０２０年０７月１７日、Ｓ医師）
従って、
（01）（02）により、
（03）
「フェブリク錠投与」は、「治療」ではなく、「予防」が「目的」であるため、
『１.治療を目的としていること』という、「第１の条件」を満たしていない。
然るに、
（04）

　　　　　　　　　　　　　　　　　　　　（２０１２年０７月０５日、Ｋ医師）
従って、
（04）により、
（05）
「２０１２年０７月０４日」に於いて、「アレルギー（眼瞼腫脹）」を起こしている。
然るに、
（06）

　　　　　　　　　　　　　（フェブリクの添付文書）
然るに、
（07）
「添付文書」にある「発疹」という「言葉」が気になったため、
令和２年７月１３日、１３時４８分～
帝人ファーマ株式会社　メディカル情報部（のＦさん）に、
「（04）２０１２年０７月０５日」の「カルテの内容」を、「読み上げて」、「確認」したところ、
２０１２年７月０５日：Ｋ医師により、フェブリクによるアレルギーＳ/Ｏ→中止。
という「処置」は、「正しい判断」であった。
という「回答」を得ている。
従って、
（04）～（07）により、
（08）
「（過敏症の既往歴があった）当該の患者」に対して、「フェブリク錠投与すること」は、
『２.承認された方法』には、当たらない。
然るに、
（09）

　　　　　　　　　　　　　　　　　　　（フェブリクの添付文書）
従って、
（09）により、
（10）
「フェブリクの添付文書」の「指示」に従う限り、
「クレアチニン（Ｃｒｅ）・尿素窒素（ＢＵＮ）」の「上昇」が認められた場合は、
「投与を中止する」など「適切な処置」を行わなければならない。
然るに、
（11）

従って、
（11）により、
（12）

従って、
（12）により、
（13）
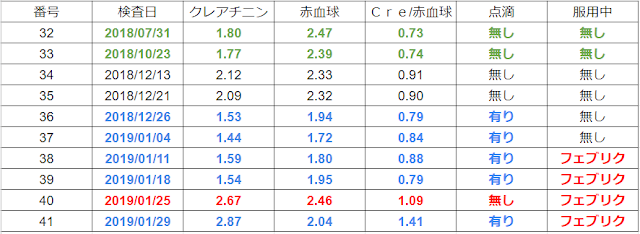
「２０１９年０１月１８日」から、
「２０１９年０１月２５日」にかけて、「点滴」を「中止」したところ、
「赤血球・尿酸」等は、「１.３倍弱」に増加したが、
「クレアチニン」は、「１.７３倍」になり、
「尿素窒素（ＢＵＮ）」に至っては、「３倍以上」になっている。
然るに、
（14）

然るに、
（15）

従って、
（14）（15）により、
（16）
Ｓ医師は、
「（１８日から２５日にかけて）水による血液濃縮が見られ、腎機能が悪化している。」
としているものの、
「クレアチニン：赤血」の「比」で見た場合も、
「１８日から２５日迄に、３８％の上昇」が、
「１８日から２９日迄に、７８％の上昇」が「確認」出来る。
然るに、
（17）

　　　　　　　　　　　　（２０１９年０１月２８日０９時１９分５０秒）
であるものの、この場合、「薬（フェブリク）の量」は、「減らされてもいない」。
従って、
（09）～（17）により、
（18）
「フェブリクの添付文書」の「指示」に従う限り、
「クレアチニン（Ｃｒｅ）・尿素窒素（ＢＵＮ）」の「上昇」が認められた場合は、
「投与を中止する」など「適切な処置」を行わなければならないが、
Ｓ医師は、そのようにはせず、何もしていない。
従って、
（01）（08）（18）により、
（19）
Ｓ医師の診療は、
（ⅰ）「本剤の成分に過敏症（アレルギー）の既往歴がある患者に、本剤を使用してはならない。」
（ⅱ）「本剤の使用中に、クレアチニン・尿素窒素の上昇が認められた場合は、本剤を使用してはならない。」

という「添付文書」の「指示」に従っていないが故に、
『２.承認された方法で行われていること』という「第２の条件」を満たしていない。
然るに、
（20）
「入院時（２０１８年１２月２１日）のオリエンテーション」の際に、

従って、
（20）により、
（21）
入院時に、看護師を通じて、
『痛風に関しては、身体に合わないで中止になった「薬（禁忌）」がある（ので、その薬は、不用意に使わないで欲しい）。』
という風に、主治医（Ｓ先生）に対して伝えてあるため、「医師の側に、債務が成立しています」。
然るに、
（22）
診療日付 ２０１９年０１月０４日 １４：５０
看護カルテ 内科 入院 主保険（０） 記載者 Ｉ.Ｎ.

従って、
（04）（05）（20）（21）（22）により、
（23）
「２０１２年０７月０４日に、眼瞼腫脹を起こしている」ので、
「それを使用しないようにと、入院時（２０１８年１２月２１日）に、医師に対して伝えていてた、フェブリクの内服開始」は、
「２０１９年０１月０４日の、翌日」です。
然るに、
（24）

然るに、
（23）（24）により、
（25）
「ザイロリック・フェブリク錠に肝障害」という「アラート」は、
「ザイロリック錠にて肝障害、フェブリク錠にてアレルギー（眼瞼腫脹）」の「マチガイ」です。
然るに、
（26）

す。また、フェブリク錠投与開始後も入院中にはフェブリク錠を投与していることを説明する機会があったこと(御提出された文書中には「2019/1/27に『フェブリク錠を1/5から使用している』との説明を受けた」記載がありますし、また、御提出された文 書に記載はありませんが2019/1/15に森田隆司様に来院していただき面談した際に尿酸 降下剤を投与している旨の説明をしております[2019/1/15 17:00 看護カルテ参 照])、御提出された文書中(8ページ)に記載されていますように、お薬手帳を病院 （令和０２年０７月、Ｓ医師）
従って、
（26）により、
（27）
（ⅰ）１月１５日は、フェブリク錠という「名前」を知らされてはいなくて、
（ⅱ）１月２７日に、フェブリク錠という「名前」を知らされては、います。
然るに、
（28） 診療日付 ２０１９年０１月１５日 １７：００
看護カルテ 内科 入院 主保険（０） 記載者 Ｙ.Ｒ．

従って、
（28）により、
（29）
（ⅲ）１月１５日に、私は、「腎機能」を心配しているが、その時点では、
（〃）「腎機能の悪化は無い」と聞いて、安堵している。
然るに、
（30）

然るに、
（21）（30）により、
（31）
入院時に、看護師を通じて、
『痛風に関しては、身体に合わないで中止になった「薬（禁忌）」がある（ので、その薬は、不用意に使わないで欲しい）。』
と伝えている一方で、
退院（して死亡する）２日前に、
脱水が原因である。「以前、使った薬」で、肝障害が出たので、その時とは、「別の薬」を使っている。
という風に、言われれば、
「前の薬」＝「６年前に使った薬」
「別の薬」＝「これまでに、１度も使ったことが無い、別の薬」
と思うことは「当然」であって、
「別の薬」＝「フェブリク」
であるとすれば、当然、「私は（債務不履行ということで）抗議」をする。
従って、
（04）（31）により、
（32）
２０１９年０１月２７日１１時４８分前後の、ナースステーションに於いて、
Ｓ医師は、私に対して、ハッキリと、「投与をしている薬」は、

　　　　　　　　　　　　　　　　　　　　（２０１２年０７月０５日、Ｋ医師）
でいう所のその「フェブリク（ によるアレルギーＳ/Ｏ→中止）」であることを、告げるべきであったし、
いずれにせよ、
（33）
２０１９年０２月０３日（葬儀の翌日）の「ｇｏｏブログ」を見ると、

となっている。
従って、
（32）（33）により、
（34）
鈴木医師は、
「前の薬」＝「１番目の薬」ではなく、
「別の薬」＝「２番目の薬」＝「フェブリク（ によるアレルギーＳ/Ｏ→中止）」を、もう一度、
「０１月０５日」から「投与」している。
ということを、「私に分かるよう」には、「説明していない」。
加えて、
（28）（29）（30）により、
（35）
「別の薬の使用」を受け入れたのは、
「検査結果」が「悪化」した「原因」は、「脱水」であるという「説明」を、「信じた」からである。
加えて、
（36）

という「事実」を、Ｓ医師が、「把握」していなければ「怠慢」であるし、「把握」したいたならば、「脱水」などという「説明」が、出来るはずが無い。
従って、
（01）（32）～（36）により、
（37）
『３.患者本人（または、保護者の）承諾があること』という「第３の条件」も、満たしてはいない。
令和０４年０７月０４日、毛利太。

「逆と対偶（美人弁護士も論理学を学んで欲しい）」。

（01）
例へば、
① 人間であるならば動物である（順）。
② 動物であるならば人間である（逆）。
③ 動物でないならば人間ではない（対偶）。
に於いて、
① ならば、② であるとは限らないが、
① ならば、③ である。
従って、
（02）
① ＰであるならばＱである（順）。
② ＱであるならばＰである（逆）。
③ ＱでないならばＰではない（対偶）。
に於いて、
① ならば、② であるとは限らないが、
① ならば、③ である。
従って、
（03）
① 　Ｐ→　Ｑ（順）
②　 Ｑ→　Ｐ（逆）
③ ～Ｑ→～Ｐ（対偶）
に於いて、
① ならば、② であるとは限らないが、
① ならば、③ である。
が、この場合、Ｐは、「集合」ではなく「命題」であるとする。
然るに、
（04）
　chi********さん2013/4/1719:51:00
　論理学について
　法学部生や法曹を目指す人にとって、論理学はとった方がいい科目ですか？？
　授業内容見ても、、
　わからないもんで（^^;）
　ベストアンサーに選ばれた回答
　doc********さん 2013/4/1720:15:10
　東大法卒のおっさんです。
　法曹をめざすのに論理学はまったく必要ありません。
　論理学的に厳密に法律を解釈しようとしても、破たんするだけです。
　法律にはそういう解釈の幅をもたせてあります。
然るに、
（05）
　瀧田早苗、二七才、東京大学法学部卒、―中略―つまり、極めて優秀なエリートだということだ。―中略―、
「正義の定義によりますね。先生は、ずっと法律を知らないと不幸になると、おっしゃっています。
　まったく同感です。でも、多くの弁護士は、法律を知っているくせに、依頼者を幸福にできていません。」
（真山仁 作、レインメーカー）
然るに、
（06）
Ｐ＝法律を知っている。
Ｑ＝不幸になる。
とすると、
① 法律を知らないと不幸になる。
② 法律を知っているくせに不幸になる。
という「命題」は、
① ～Ｐ→Ｑ
②　 Ｐ→Ｑ
という風に、書くこと出来る。
従って、
（05）（06）により、
（07）
先生は、　ずっと法律を知らないと、　　　依頼者は不幸になると、おっしゃっていますが、
多くの弁護士は、法律を知っているくせに、依頼者を不幸にしている。
という風に述べていることから、
瀧田早苗は、
① ～Ｐ→Ｑ
②　 Ｐ→Ｑ
に於いて、
①と②は『矛盾』すると、言っている。
然るに、
（08）
① ～Ｐ→　Ｑ
②　 Ｐ→　Ｑ
③ ～Ｐ→～Ｑ
に於いて、
①と② は『矛盾』しないが、
①と③ は『矛盾』する。
従って、
（07）（08）により、
（09）
瀧田早苗は、
②　 Ｐ→　Ｑ
③ ～Ｐ→～Ｑ
に於いて、
② ならば、③ である。
と、言っている。
然るに、
（10）
②　 Ｐ→　Ｑ
③ ～Ｐ→～Ｑ
④ 　Ｑ→　Ｐ
に於いて、
③＝④ は「対偶」である。
従って、
（09）（10）により、
（11）
瀧田早苗は、
② Ｐ→Ｑ（順）
③ Ｑ→Ｐ（逆）
に於いて、
② ならば、③ である（逆も真である）。
と言っている。
従って、
（05）～（11）により、
（12）
瀧田早苗（二七才、東京大学法学部卒、ヤメ検）は、
③ Ｑ→Ｐ
③ 不幸になるならば、法律を知っている。
と、言っている。
従って、
（06）（07）（12）により、
（13）
瀧田早苗（二七才、東京大学法学部卒、ヤメ検）は、
① 法律を知らないと不幸になる。
② 法律を知っているくせに不幸になる。
に於いて、すなわち、
① ～Ｐ→Ｑ
②　 Ｐ→Ｑ
に於いて、
①と② は『矛盾』する。
としたことによって、
③ Ｑ→Ｐ
③ 不幸になるならば、法律を知っている。
と、言っている。
従って、
（06）（07）（13）により、
（14）
瀧田早苗（二七才、東京大学法学部卒、ヤメ検）は、
① ～Ｐ→Ｑ
②　 Ｐ→Ｑ
③ 　Ｑ→Ｐ
に於いて、
①と② は『矛盾』するとしたことによって、
① 法律を知らないと不幸になるが、
③ 不幸になると、法律を知っている。
と言っている。
従って、
（14）により、
（15）
瀧田早苗（二七才、東京大学法学部卒、ヤメ検）は、
① ～Ｐ→Ｑ
②　　　 Ｑ→Ｐ
により、
① ～Ｐ→Ｐ
① 法律を知らないならば、法律を知っている。
と言っている。
然るに、
（16）
１　　（１）　～Ｐ→Ｐ　Ａ
１　　（２）～～Ｐ∨Ｐ　１含意の定義
　３　（３）～～Ｐ　　　Ａ
　３　（４）　　Ｐ　　　３ＤＮ
　　５（５）　　　　Ｐ　Ａ
１　　（６）　　　　Ｐ　１３４５５∨Ｅ
１　　（７）～～Ｐ∨Ｐ　６∨Ｉ
１　　（５）　～Ｐ→Ｐ　７含意の定義
従って、
（15）（16）により、
（17）
瀧田早苗（二七才、東京大学法学部卒、ヤメ検）は、
① 法律を知らないならば、法律を知っている。
① 法律を知っている。
と、言っている。
従って、
（05）～（17）により、
（18）
「論理学的」に言えば、「小説」の中の、
瀧田早苗（二七才、東京大学法学部卒、ヤメ検、美人）は、「賢い（優秀である）」とは言えない。
従って、
（04）（18）により、
（19）
「人の運命を左右する」のだから、
「法曹をめざすのに論理学はまったく必要ありません。」
とは言わずに、願わくは、
「法律家こそが、論理学を学ぶべきである。」
ｃｆ.
法律家の言う「論理」
法律家、つまり弁護士とか裁判官とか検事などは、自分たちが論理を得意とすると思っているようです。
でも、他分野の学問にそれなりに触れた人にとっては、法律家が論理を理解しているようには思えないと思います。
むしろ、法律学というのは極めて非論理的なものという印象を抱くのではないでしょうか。
私自身も、法律を学び始めた当初は、その中で使われる「論理的」の意味をつかみ、それに慣れるのに、苦労しました。
（横浜の弁護士ブログ）
令和０４年０７月２９日、毛利太。

「逆と対偶」と「誤診」について。

（01）
赤血球が増える場合には、絶対的な多血症と、検査上数値が高くなる見かけ上の赤血球増多症の場合があります。
見かけ上の場合は、血液が濃縮されることによって起こります（臨床検査ＡtoＺ）。
従って、
（01）により、
（02）
「脱水（血液濃縮）」起こすと、「赤血球（ＲＢＣ）の値」は「上昇」する。
然るに、
（03）

従って、
（02）（03）により、
（04）
「脱水（血液濃縮）」を起こすと、「赤血球・ヘモグロビン・ヘマトリック・アルブミン・クレアチニン・ＢＵＮ」等の「値」が「上昇」し、
「点滴（輸液）」をすると、「脱水（血液濃縮）」が「解消」されて、「これらの数値」が「下がり」ます。
然るに、
（05）
①  Ｐ→（Ｑ→Ｒ）
②（Ｑ→Ｒ）→Ｐ
に於いて、すなはち、
① Ｐであるならば（ＱならばＲである）。
②（ＱならばＲである）ならばＰである。
において、
① は、② の「逆」であり、
② は、① の「逆」である。
然るに、
（06）
（ⅱ）
１　（１）　（Ｑ→　Ｒ）→Ｐ　Ａ
　２（２）～（Ｑ＆～Ｒ）　　　Ａ
　２（３）　～Ｑ∨　Ｒ　　　　２ド・モルガンの法則
　２（４）　　Ｑ→　Ｒ　　　　３含意の定義
１２（５）　　　　　　　　Ｐ　１４ＭＰＰ
１　（６）～（Ｑ＆～Ｒ）→Ｐ　２５ＣＰ
（ⅲ）
１　（１）～（Ｑ＆～Ｒ）→Ｐ　Ａ
　２（２）　　Ｑ→　Ｒ　　　　Ａ
　２（３）　～Ｑ∨　Ｒ　　　　２含意の定義
　２（４）～（Ｑ＆～Ｒ）　　　３ド・モルガンの法則
１２（５）　　　　　　　　Ｐ　１４ＭＰＰ
１　（６）　（Ｑ→　Ｒ）→Ｐ　２５ＣＰ
従って、
（06）により、
（07）
②   （Ｑ→  Ｒ）→Ｐ
③ ～（Ｑ＆～Ｒ）→Ｐ
に於いて、
②＝③ である。
従って、
（05）（06）（07）により、
（08）
① 　  Ｐ→（Ｑ→  Ｒ）
② ～（Ｑ＆～Ｒ）→Ｐ
に於いて、
① は、② の「逆」であり、
② は、① の「逆」である。
然るに、
（09）
（ⅰ）
１　　　（１）　Ｐ→（Ｑ→　Ｒ）　Ａ
　２　　（２）　　　　Ｑ＆～Ｒ　　Ａ
　　３　（３）　　　　Ｑ→　Ｒ　　Ａ
　２　　（４）　　　　Ｑ　　　　　＆Ｉ
　２３　（５）　　　　　　　Ｒ　　３４ＭＰＰ
　２　　（６）　　　　　　～Ｒ　　２＆Ｅ
　２３　（７）　　　　Ｒ＆～Ｒ　　５６＆Ｉ
　２　　（８）　　～（Ｑ→　Ｒ）　３７ＲＡＡ
１２　　（９）～Ｐ　　　　　　　　１８ＭＴＴ
１　　　（ア）（Ｑ＆～Ｒ）→～Ｐ　２９ＣＰ
（ⅲ）
１　　　（１）（Ｑ＆～Ｒ）→～Ｐ　Ａ
　　　２（２）　　　　　　　　Ｐ　Ａ
　　　２（３）　　　　　　～～Ｐ　２ＤＮ
１　　２（４）　～（Ｑ＆～Ｒ）　　１３ＭＴＴ
１　　２（５）　　～Ｑ∨　Ｒ　　　４、ド・モルガンの法則
１　　２（６）　　　Ｑ→　Ｒ　　　５含意の定義
１　　　（７）Ｐ→（Ｑ→　Ｒ）　　２６ＣＰ
従って、
（09）により、
（10）
① 　  Ｐ→（Ｑ→    Ｒ）
② ～（Ｑ＆～Ｒ）→  Ｐ
③　 （Ｑ＆～Ｒ）→～Ｐ
に於いて
①と② は「逆（converse）」であって、
①＝③ は「対偶（contraposition）」である。
従って、
（11）
Ｐ＝脱水である。
Ｑ＝点滴をする。
Ｒ＝数値が下がる。
として、
① 脱水であるならば（点滴をすると、数値が下がる）。
②（点滴をして数値が下がらない）ということがないならば、脱水である。
③（点滴をして数値が下がらない）ならば、脱水ではない。
に於いて、
①と② は「逆（converse）」であって、
①＝③ は「対偶（contraposition）」である。
従って、
（11）により、
（12）
① 脱水であるならば（点滴をすれば、数値が下がる）。
②（点滴をして数値が下がる）ならば、脱水である。
③（点滴をして数値が下がらない）ならば、脱水ではない。
に於いて、
①と② は「逆（converse）」であって、
①＝③ は「対偶（contraposition）」である。
然るに、
（13）
ある命題とその逆の真偽は、必ずとも一致しない（逆は必ずしも真ならず）。
この表現は日常生活や数学の中でことわざのように使用されることがある（ウィキペディア）。
然るに、
（14）
数学では、元の命題「ＡならばＢ」の証明が難しくても、その対偶「ＢでないならばＡでない」の証明は比較的易しい場合がある。両者の証明可能性は一致するので、対偶「ＢでないならばＡでない」を示すことにより「ＡならばＢ」を証明できる。これを対偶論法とよぶ。同様に、「ＢならばＡである」を示すことにより「ＡでないならばＢでない」を証明することもできる（ウィキペディア）。
従って、
（12）（13）（14）により、
（15）
① 脱水であるならば（点滴をすれば、数値が下がる）。
②（点滴をして数値が下がる）ならば、脱水である。
③（点滴をして数値が下がらない）ならば、脱水ではない。
に於いて、
① が「真（本当）」であるとしても、
② が「偽（ウソ）」であることは、「可能」であるが、
① が「真（本当）」であらならば、
③ は、必然的に「真（本当）」である。
然るに、
（03）により、
（16）
① 脱水であるならば（点滴をすれば、数値が下がる）。
ということは、「真（本当）」である。
従って、
（15）（16）により、
（17）
②（点滴をして数値が下がる）としても、　「脱水」であるかどうかは、　「不明」であるが、
③（点滴をして数値が下がらない）ならば、「脱水」ではないということは「確実」である。
従って、
（15）（16）（17）により、
（18）
① 脱水であるならば（点滴をすれば、数値が下がる）。
②（点滴をして数値が下がらない）ならば、脱水ではない。
に於いて、
① は「真（本当）」であって、
①＝② は「対偶（contraposition）」であるが故に、
② は「真（本当）」である。
然るに、
（19）

従って、
（19）により、
（20）

従って、
（18）（19）（20）により、
（21）
②（点滴をして数値が下がらない）ならば、脱水ではない。
という「理由」により、

という「診断」が、『誤診』であった。
ということは、「確実」です。
然るに、
（22）

従って、
（21）（22）により、
（23）
「２０１９年０１月２５日の血液検査」により、
「脱水による血液濃縮の傾向がみられた」とは言うものの、
「赤血球」で見ると、
２０１８年０２月２０日（２.７２）は、健康で、点滴無し。
２０１８年０５月１５日（２.４４）も、健康で、点滴無し。
２０１８年０７月３１日（２.４７）も、健康で、点滴無し。
２０１８年１０月２３日（２.３９）も、健康で、点滴無し。
であるため、
２０１９年０１月２５日（２.４６）も、健康で、点滴無し。
である。
従って、
（23）により、
（24）
「２０１９年０１月２５日の血液検査」により、
「脱水による血液濃縮の傾向がみられた」とは言うものの、
「赤血球」で見ると、
「点滴」を「中止」したら、「以前の、健康な頃の数値」に戻っただけである。
ということに、過ぎない。
従って、
（23）（24）により、
（25）
「２０１９年０１月２５日の血液検査」により、
「脱水による血液濃縮の傾向がみられた」と言うのであれば、その場合は、
２０１８年０２月２０日（２.７２）は、健康で、点滴無し。
２０１８年０５月１５日（２.４４）も、健康で、点滴無し。
２０１８年０７月３１日（２.４７）も、健康で、点滴無し。
２０１８年１０月２３日（２.３９）も、健康で、点滴無し。
という「直近」の、「（悪性貧血は、父の持病に関する）データ」に目を通していなかった。
ということになる。
従って、
（25）により、
（26）
「逆（？）に言う」と、
２０１８年０２月２０日（２.７２）は、健康で、点滴無し。
２０１８年０５月１５日（２.４４）も、健康で、点滴無し。
２０１８年０７月３１日（２.４７）も、健康で、点滴無し。
２０１８年１０月２３日（２.３９）も、健康で、点滴無し。
という「直近」の、「（悪性貧血は、父の持病に関する）データ」に目を通していたならば、
「脱水による血液濃縮の傾向がみられた」という「誤診」は、「回避」出来た。
という、ことになる。
然るに、
（27）
患者に対して医師が薬を投与したときに、蕁麻疹が生じる等の症状が出たときには、薬の副作用の疑いもあります。このとき、同じ薬を投与し続ければ、さらに重い副作用が発生して深刻な影響が生じることを予見し、薬の投与を中断したり、薬の種類を変更したりして、深刻な影響が生じるという結果を回避できる場合があります。このような予見可能性と結果回避可能性は、注意義務違反（過失）の前提として必要とされるものです（医学博士 弁護士 金﨑浩之）。
従って、
（19）（20）（26）（27）により、
（28）
「２０１９年０１月２５日の血液検査」で、「急性腎不全」を起きていたにも拘わらず、
「フェブリクの添付文書の指示」に従わず、
「２０１９年０１月２９日」に、死亡するに至ったという「結果」に対して、Ｓ.Ｕ.医師には、「注意義務違反（過失）」があった。
という風に、私自身は、考えます。
然るに、
（29）
医療過誤・医療事故について弁護士が答えるよくある質問Ｑ＆Ａ
Ｑ５４.
鑑定料は幾ら位ですか？鑑定料は誰が負担するのですか？
Ａ５４.
鑑定料は、鑑定事項により増減はありますが、基本は５０万円で、補充鑑定を行うなど鑑定人の負担が大きいときは１０万円が加算される場合が多いです。鑑定料は、鑑定申請をした側が負担しますが、通常、原告と被告の双方から鑑定申請して鑑定料を折半します。
というわけで、
（30）
弁護士に相談したところ、その先生も言うことには、「医療裁判」の場合は、「医療事故（と原告が考える）の内容」を、第三者の医師が鑑定することになる。
とのことでした。
然るに、
（31）
― ＃＃＃＃の主治医であったＫ.Ｕ.先生に、「質問」があります。―
（01） ＃＃医師（外科）からの院内紹介にて、
２０１２年０７月１８日より、
２０１８年１２月１３日まで、Ｋ.Ｕ.先生に、主治医を務めて頂き、
２０１９年０２月０５日には、Ｋ.Ｕ.先生の診察を予定していた、
＃＃＃＃（患者ID0000#######）の遺族の、＃＃＃＃と申します。
（令和０４年０７月０８日に、送付した、質問状の、書き出し）
従って、
（25）（29）（30）（31）により、
（32）
２０１８年０２月２０日（２.７２）は、Ｋ.Ｕ.先生が主治医。
２０１８年０５月１５日（２.４４）も、Ｋ.Ｕ.先生が主治医。
２０１８年０７月３１日（２.４７）も、Ｋ.Ｕ.先生が主治医。
２０１８年１０月２３日（２.３９）も、Ｋ.Ｕ.先生が主治医。
と「比較」して、
２０１９年０１月２５日（２.４６）は、Ｋ.Ｕ.先生ではなく、Ｓ.Ｕ.先生が主治医。
の場合は、「脱水」と言えるのか（？）、
という「質問」をするために、わざわざ、６０万円も使うのであれば、当然、
そのときに主治医であった、Ｋ.Ｕ.先生に、「質問」しないわけには、行かない。
従って、
（32）により、
（33）
＃＃医師（外科）からの院内紹介にて、
２０１２年０７月１８日より、
２０１８年１２月１３日まで、主治医を務めて頂いた、Ｋ.Ｕ.先生からは、
２０１８年０２月２０日（２.７２）
２０１８年０５月１５日（２.４４）
２０１８年０７月３１日（２.４７）
２０１８年１０月２３日（２.３９）
を含めて、
＃＃＃＃（患者ID0000#######）に「脱水」が有った。
という「話」は聞いていないし、
２０１２年０６月１８日から、
２０１８年１２月１３日までの「カルテ」にも、「脱水」という「文字」は有りません。
従って、
（34）
Ｋ.Ｕ.先生が、上司である、副院長の、
Ｓ.Ｕ.先生を、庇って、「赤血球」の、
２０１９年０１月２５日（２.４６） という「値」を以てしても、「脱水はあった」と、「強弁」することは、「不可能」であると、知った上で、
― ＃＃＃＃の主治医であったＫ.Ｕ.先生に、「質問」があります。―
という「質問書」を、

でいうところの、Ｋ弁護士宛てに、送付したものの、今日で、２０日を過ぎた現在、「返信」はありませんが、「前回」は確か、「返事」が来るまでに「３か月」を要しています。
（35）
「法律家の方」たちが、
① 脱水であるならば（点滴をすると、数値が下がる）。
②（点滴をして数値が下がらない）ということがないならば、脱水である。
③（点滴をして数値が下がらない）ならば、脱水ではない。
に於いて、
①と② は「逆（converse）」であって、
①＝③ は「対偶（contraposition）」である。
ということを、「理解」出来ないはずがないと、思いたいのですが、その一方で、
　chi********さん2013/4/1719:51:00
　論理学について
　法学部生や法曹を目指す人にとって、論理学はとった方がいい科目ですか？？
　授業内容見ても、、
　わからないもんで（^^;）
　ベストアンサーに選ばれた回答
　doc********さん 2013/4/1720:15:10
　東大法卒のおっさんです。
　法曹をめざすのに論理学はまったく必要ありません。
　論理学的に厳密に法律を解釈しようとしても、破たんするだけです。
　法律にはそういう解釈の幅をもたせてあります。
という「言い方」に、「不安」を覚えます。
（36）
① 脱水であるならば（点滴をすると、数値が下がる）。
②（点滴をして数値が下がらない）ならば、脱水ではない。
①＝② は「対偶（contraposition）」である。
ということと、

2 刑事責任
医療過誤は場合によっては業務上過失致死傷罪（刑法211条）に該当することがありますが、民事損害賠償責任とは異なり、国家刑罰権の発動ですので、患者が死亡しかつ過誤が初歩的ミスの場合のような重大な不注意で患者が死亡した場合に限って起訴されることが多いのが実情です。
（学陽書房、医療事故の法律相談〈全訂版〉、2009年、12頁）
ということからすれば、Ｓ.Ｕ.先生は、「（将棋で言えば）詰んでいる」と、私自身は思っています。
令和０４年０７月２８日、毛利太。

「等号を含む述語計算」の「例題（E.J.レモン）」。

（01）
２ つぎの論証を等号を含む述語計算の記号に翻訳し、それに対応する連式の妥当性を示すことによって、論証の健全性を証明せよ。
２ Prove the soundness of the following arguments by translating them into the symbolism of the predicate calculus with identity and showing the validity of the corresponding sequents;
（ａ）すべての殺人者は精神異常である。ジーキルは殺人者である。ジーキルはハイドである。故にハイドは精神異常である。
（ｂ）いかなる殺人者も精神が正常でない。ジーキルは殺人者である。ハイドは精神が正常である。故にジーキルはハイドではない。
（ｃ）トムとジェーンのみ（Only Tom and Jane）がダンスをしている。トムとジェーンはどちらもツイストをしている。故にすべてのダンスをしているものはツイストをしている。
（ｄ）多くとも１人（at most one）の無法な国家主席がいる。毛沢東は無法な国家主席である。ジョンソンは毛沢東ではない。故にジョンソンは無法な国家主席ではない。
（E.J.レモン 著、竹尾治一郎・浅野楢英 訳、論理学初歩、1973年、２１５頁）
　―「私による解答と解説」―
（02）
（ａ）すべての殺人者は精神異常である。ジーキルは殺人者である。ジーキルはハイドである。故にハイドは精神異常である。
に於いて、
ｊ＝ジーキル（固有名）
ｈ＝ハイド　（固有名）
とすると、
１　　（１）∀ｘ（殺人者ｘ→精神異常ｘ）　Ａ
　２　（２）殺人者ｊ　　　　　　　　　　　Ａ
　　３（３）　　　ｊ＝ｈ　　　　　　　　　Ａ
１　　（４）殺人者ｊ→精神異常ｊ　　　　　１ＵＥ
１２　（５）　　　　　精神異常ｊ　　　　　２４ＭＰＰ
１２　（６）　　　　　精神異常ｈ　　　　　３５＝Ｅ
（〃）
「どのやうな殺人者であっても、例外なく精神異常である。」
とするならば、
「ジーキルが殺人者であれば、ジーキルは精神異常である。」
ところが、
「ジーキル（ｊ）とハイド（ｈ）は「同一人物（the same person）」である。
従って、
「ハイド（ジーキル）」は精神異常である。
（03）
（ｂ）いかなる殺人者も精神が正常でない。ジーキルは殺人者である。ハイドは精神が正常である。故にジーキルはハイドではない。
に於いて、
ｊ＝ジーキル（固有名）
ｈ＝ハイド　（固有名）
とすると、
１　　　（１）∀ｘ（殺人者ｘ→～正常ｘ）　Ａ
　２　　（２）殺人者ｊ　　　　　　　　　　Ａ
　　３　（３）正常ｈ　　　　　　　　　　　Ａ
１　　　（４）殺人者ｊ→～正常ｊ　　　　　１ＵＥ
１２　　（５）　　　　　～正常ｊ　　　　　２４ＭＰＰ
　　　４（６）ｊ＝ｈ　　　　　　　　　　　Ａ
１２　４（７）　　　　　正常ｊ　　　　　　３６＝Ｅ
１２　４（８）～正常ｊ＆正常ｊ　　　　　　５７＆Ｉ
１２　　（９）ｊ≠ｈ　　　　　　　　　　　４８ＲＡＡ
（〃）
「どのやうな殺人者であっても、例外なく精神が正常でない。」
とするならば、
「ジーキルが殺人者であれば、ジーキルは精神が正常ではない。」
ところで、
「ジーキルは殺人者である。」
従って、
「ジーキルは精神が正常ではない。」
然るに、
「ハイドは精神が正常である。」
従って、
「ジーキルとハイドが同一人物（the same person）」である。
とするならば、
「ジーキルは精神が異常であって、尚且つ、正常である。」
ということになって、「矛盾」する。
従って、
「ジーキル（ｊ）とハイド（ｈ）は「同一人物（the same person）」ではない。
（04）
（ｃ）トムとジェーンのみ（Only Tom and Jane）がダンスをしている。トムとジェーンはどちらもツイストをしている。故にすべてのダンスをしているものはツイストをしている。
に於いて、
ｔ＝トム　　（固有名）
ｈ＝ジェーン（固有名）
とすると、
１　　　　（１）∀ｘ｛～（ｘ＝ｔ∨ｘ＝ｊ）→～ダンスｘ｝　Ａ
１　　　　（２）　　　～（ａ＝ｔ∨ａ＝ｊ）→～ダンスａ　　１ＵＥ
　　３　　（３）　　　　　　　　　　　　　　　ダンスａ　　Ａ
　　３　　（４）　　　　　　　　　　　　　～～ダンスａ　　３ＤＮ
１　３　　（５）　　　　　ａ＝ｔ∨ａ＝ｊ　　　　　　　　　２４ＭＴＴ
　　　６　（６）　　　ツイストｔ＆ツイストｊ　　　　　　　Ａ
　　　６　（７）　　　ツイストｔ　　　　　　　　　　　　　６＆Ｅ
　　　８　（８）　　　　　ａ＝ｔ　　　　　　　　　　　　　Ａ
　　６８　（９）　　　ツイストａ　　　　　　　　　　　　　７８＝Ｅ
　　６　　（ア）　　　　　　　　　ツイストｊ　　　　　　　６＆Ｅ
　　　　イ（イ）　　　　　　　　　　　ａ＝ｊ　　　　　　　Ａ
　　６　イ（ウ）　　　　　　　　　ツイストａ　　　　　　　アイ＝Ｅ
１３６　　（エ）　　　ツイストａ　　　　　　　　　　　　　５８９イウ∨Ｅ
１　６　　（オ）　　　ダンスａ→　ツイストａ　　　　　　　３エＣＰ
１　６　　（カ）∀ｘ（ダンスｘ→　ツイストｘ）　　　　　　オＵＩ
（〃）
「誰であれ、（トムか、ジェーン）でなければ、ダンスをしていない。」
然るに、
「トムも、ジェーンも、ツイストをしている。」
従って、
「ツイストをしている人以外は、ダンスをしていない。」
従って、
「すべてのダンスをしているものはツイストをしている。」
（05）
（ｄ）多くとも１人（at most one）の無法な国家主席がいる。毛沢東は無法な国家主席である。ジョンソンは毛沢東ではない。故にジョンソンは無法な国家主席ではない。
に於いて、
ｍ＝毛沢東　　（固有名）。
ｊ＝ジョンソン（固有名）。
Ｆ＝無法な国家主席である（といふ述語文字）。
とすると、
１　　（１）～∃ｘ∃ｙ（Ｆｘ＆Ｆｙ＆ｘ≠ｙ）　Ａ
１　　（２）∀ｘ～∃ｙ（Ｆｘ＆Ｆｙ＆ｘ≠ｙ）　１量化子の関係
１　　（３）∀ｘ∀ｙ～（Ｆｘ＆Ｆｙ＆ｘ≠ｙ）　２量化子の関係
１　　（４）　　∀ｙ～（Ｆｍ＆Ｆｙ＆ｍ≠ｙ）　３ＵＥ
１　　（５）　　　　～（Ｆｍ＆Ｆｊ＆ｍ≠ｊ）　４ＵＥ
１　　（６）　　～｛（Ｆｍ＆Ｆｊ）＆ｍ≠ｊ｝　５結合法則
１　　（７）　　　～（Ｆｍ＆Ｆｊ）∨ｍ＝ｊ　　６ド・モルガンの法則
１　　（８）　　　　（Ｆｍ＆Ｆｊ）→ｍ＝ｊ　　７含意の定義
　９　（９）　　　　　Ｆｍ　　　　　　　　　　Ａ
　　ア（ア）　　　　　　　　　　　　ｍ≠ｊ　　Ａ
１　ア（イ）　　　～（Ｆｍ＆Ｆｊ）　　　　　　８アＭＴＴ
１　ア（ウ）　　　～Ｆｍ∨～Ｆｊ　　　　　　　イ、ド・モルガンの法則
１　ア（エ）　　　　Ｆｍ→～Ｆｊ　　　　　　　ウ含意の定義
１９ア（オ）　　　　　　　～Ｆｊ　　　　　　　９エＭＰＰ
（〃）
（ⅰ）
① 少なくとも２人＝２人以上。
② 多くとも、１人＝１人以下（１人か、０人）。
であるため、
① の「否定」が、② である。
然るに、
（ⅱ）
① ∃ｘ∃ｙ（Ｆｘ＆Ｆｙ＆ｘ≠ｙ）
② 少なくとも２人以上の無法な国家主席がいる。
に於いて、
①＝② である。
従って、
（ⅰ）（ⅱ）により、
（ⅲ）
① ～∃ｘ∃ｙ（Ｆｘ＆Ｆｙ＆ｘ≠ｙ）
② 多くとも１人（at most one）の無法な国家主席がいる。
に於いて、
①＝② である。
然るに、
（ⅳ）
（α）
１　　（１）～∃ｘ∃ｙ（Ｆｘ＆Ｆｙ＆ｘ≠ｙ）　Ａ
１　　（２）∀ｘ～∃ｙ（Ｆｘ＆Ｆｙ＆ｘ≠ｙ）　１量化子の関係
１　　（３）∀ｘ∀ｙ～（Ｆｘ＆Ｆｙ＆ｘ≠ｙ）　２量化子の関係
１　　（４）　　　３ＵＥ
１　　（５）　　　　～（Ｆａ＆Ｆｂ＆ａ≠ｂ）　４ＵＥ
１　　（６）　　～｛（Ｆａ＆Ｆｂ）＆ａ≠ｂ｝　５結合法則
１　　（７）　　　～（Ｆａ＆Ｆｂ）∨ａ＝ｂ　　６ド・モルガンの法則
１　　（８）　　　　（Ｆａ＆Ｆｂ）→ａ＝ｂ　　７含意の定義
　９　（９）　　　　　　　　　　　　ａ≠ｂ　　Ａ
１９　（ア）　　　～（Ｆａ＆Ｆｂ）　　　　　　８９ＭＴＴ
１９　（イ）　　　　～Ｆａ∨～Ｆｂ　　　　　　ア、ド・モルガンの法則
１９　（ウ）　　　　　Ｆａ→～Ｆｂ　　　　　　イ、含意の定義
１　　（エ）ａ≠ｂ→（Ｆａ→～Ｆｂ）　　　　　９ウＣＰ
　　オ（オ）ａ≠ｂ＆　Ｆａ　　　　　　　　　　Ａ
　　オ（カ）ａ≠ｂ　　　　　　　　　　　　　　オ＆Ｅ
１　オ（キ）　　　　　Ｆａ→～Ｆｂ　　　　　　エカＭＰＰ
　　オ（ク）　　　　　Ｆａ　　　　　　　　　　オ＆Ｅ
１　オ（ケ）　　　　　　　　～Ｆｂ　　　　　　キクＭＰＰ
１　　（コ）　　　　　ａ≠ｂ＆Ｆａ→～Ｆｂ　　オケＣＰ
１　　（サ）　　∀ｙ（ａ≠ｙ＆Ｆａ→～Ｆｙ）　コＵＩ
１　　（シ）∀ｘ∀ｙ（ｘ≠ｙ＆Ｆｘ→～Ｆｙ）　サＵＩ
（β）
１　　（１）∀ｘ∀ｙ（ｘ≠ｙ＆Ｆｘ→～Ｆｙ）　Ａ
１　　（２）　　∀ｙ（ａ≠ｙ＆Ｆａ→～Ｆｙ）　１ＵＥ
１　　（３）　　　　　ａ≠ｂ＆Ｆａ→～Ｆｂ　　１ＵＥ
　４　（４）　　　　　　　　　Ｆａ＆　Ｆｂ　　Ａ
　４　（５）　　　　　　　　　　　　　Ｆｂ　　４＆Ｅ
　４　（６）　　　　　　　　　　　～～Ｆｂ　　５ＤＮ
１４　（７）　　　～（ａ≠ｂ＆　Ｆａ）　　　　３６ＭＴＴ
１４　（８）　　　　　ａ＝ｂ∨～Ｆａ　　　　　７ド・モルガンの法則
１４　（９）　　　　　～Ｆａ∨ａ＝ｂ　　　　　８交換法則
１４　（ア）　　　　　　Ｆａ→ａ＝ｂ　　　　　９含意の定義
　４　（イ）　　　　　　Ｆａ　　　　　　　　　４＆Ｅ
１４　（ウ）　　　　　　　　　　ａ＝ｂ　　　　アイＭＰＰ
１　　（エ）　　　　（Ｆａ＆Ｆｂ）→ａ＝ｂ　　４ウＣＰ
１　　（オ）　　　～（Ｆａ＆Ｆｂ）∨ａ＝ｂ　　エ含意の定義
１　　（カ）　　～｛（Ｆａ＆Ｆｂ）＆ａ≠ｂ｝　オ、ド・モルガンの法則
１　　（キ）　　　　～（Ｆａ＆Ｆｂ＆ａ≠ｂ）　カ結合法則
１　　（ク）　　∀ｙ～（Ｆａ＆Ｆｙ＆ａ≠ｙ）　キＵＩ
１　　（ケ）∀ｘ∀ｙ～（Ｆｘ＆Ｆｙ＆ｘ≠ｙ）　クＵＩ
１　　（コ）∀ｘ～∃ｙ（Ｆｘ＆Ｆｙ＆ｘ≠ｙ）　ケ量化子の関係
１　　（サ）～∃ｘ∃ｙ（Ｆｘ＆Ｆｙ＆ｘ≠ｙ）　コ量化子の関係
従って、
（ⅲ）（ⅳ）により、
（ⅴ）
① ～∃ｘ∃ｙ（Ｆｘ＆Ｆｙ＆ｘ≠ｙ）
② 多くとも１人しか無法な国家主席はいない。
③ ∀ｘ∀ｙ（ｘ≠ｙ＆Ｆｘ→～Ｆｙ）
④ ｘとｙが誰であれ、ｘとｙが「同一人物」ではなく、ｘが無法な国家主席であるならば、ｙは無法な国家主席ではない。
に於いて、
①＝②＝③＝④ である。
従って、
（ⅴ）により、
（ⅵ）
（ｄ）多くとも１人（at most one）の無法な国家主席がいる。毛沢東は無法な国家主席である。ジョンソンは毛沢東ではない。故にジョンソンは無法な国家主席ではない。
という「推論」は、「妥当」である。
従って、
（01）～（05）により、
（06）
（ａ）すべての殺人者は精神異常である。ジーキルは殺人者である。ジーキルはハイドである。故にハイドは精神異常である。
（ｂ）いかなる殺人者も精神が正常でない。ジーキルは殺人者である。ハイドは精神が正常である。故にジーキルはハイドではない。
（ｃ）トムとジェーンのみ（Only Tom and Jane）がダンスをしている。トムとジェーンはどちらもツイストをしている。故にすべてのダンスをしているものはツイストをしている。
（ｄ）多くとも１人（at most one）の無法な国家主席がいる。毛沢東は無法な国家主席である。ジョンソンは毛沢東ではない。故にジョンソンは無法な国家主席ではない。
という「論証の健全性」は、「等号を含む述語計算（The predicate calculus with identity）」によって「証明」出来る。
ということが、「証明」出来た。
令和０４年０７月２６日、毛利太。

「日本語」で考へた場合の「弱選言（両立的選言）」と「強選言（排他的選言）」。

（01）
① Ｐ∨Ｑ＝ＰとＱの、少なくとも、一方は「真」である。
② Ｐ▽Ｑ＝ＰとＱの、「真・偽」は、一致しない。
に於いて、
① は「弱選言（両立的選言）」である。
② は「強選言（排他的選言）」である。
然るに、
（02）
① Ｐが「偽」であって、その上、Ｑも「偽」であるならば、（ＰとＱの、少なくとも一方は「真」である）といふことには、ならないし、
② Ｐが「偽」であって、その上、Ｑも「偽」であるとしても（ＰとＱの「真・偽」は一致しない）といふことには、ならない。
従って、
（01）（02）により、
（03）
① Ｐ∨Ｑ であって、尚且つ、Ｐが「偽」であるならば、Ｑは「真」であって、
② Ｐ▽Ｑ であって、尚且つ、Ｐが「偽」であるならば、Ｑは「真」である。
然るに、
（04）
① Ｐ∨Ｑ，～Ｐ├ Ｑ
② Ｐ▽Ｑ，～Ｐ├ Ｑ
といふ「連式」は、
① Ｐ∨Ｑ であって、尚且つ、Ｐは「偽」である。故に、Ｑは「真」である。
② Ｐ▽Ｑ であって、尚且つ、Ｐは「偽」である。故に、Ｑは「真」である。
といふ「意味」である。
従って、
（03）（04）により、
（05）
① Ｐ∨Ｑ，～Ｐ├ Ｑ
② Ｐ▽Ｑ，～Ｐ├ Ｑ
といふ「推論（選言三段論法）」は、両方とも、「妥当」である。
従って、
（01）（05）により、
（06）
①「（両立的）選言三段論法」は「妥当」であって、
②「（排他的）選言三段論法」も「妥当」である。
然るに、
（01）により、
（07）
① Ｐ∨Ｑ＝ＰとＱの、少なくとも、一方は「真」である。
② Ｐ▽Ｑ＝ＰとＱの、「真・偽」は、一致しない。
といふことからすれば、、
① であれば、「Ｐは真、Ｑも真」であることは、「許容」され、
② であれば、「Ｐは真、Ｑも真」であることは、「許容」されない。
従って、
（07）により、
（08）
① Ｐ∨Ｑ，Ｐ├ ～Ｑ
② Ｐ▽Ｑ，Ｐ├ ～Ｑ
といふ「連式」に於いて、
① は「妥当」ではないが、
② は「妥当」である。
令和０４年０７月２２日、毛利太。

「強選言（排他的選言）」と「弱選言（両立的選言）」と「選言三段論法」（Ⅲ）。

（01）
（ⅰ）
１　　（１）　～（Ｐ⇔Ｑ）　　　　　　　　　Ａ
１　　（２）～｛（Ｐ→Ｑ）＆　（Ｑ→Ｐ）｝　１Ｄｆ.⇔
１　　（３）　～（Ｐ→Ｑ）∨～（Ｑ→Ｐ）　　２ド・モルガンの法則
　４　（４）　～（Ｐ→Ｑ）　　　　　　　　　Ａ
　４　（５）～（～Ｐ∨Ｑ）　　　　　　　　　４含意の定義
　４　（６）　（Ｐ＆～Ｑ）　　　　　　　　　５ド・モルガンの法則
　４　（７）　（Ｐ＆～Ｑ）∨（Ｑ＆～Ｐ）　　６∨Ｉ
　　８（８）　　　　　　　　～（Ｑ→Ｐ）　　Ａ
　　８（９）　　　　　　　～（～Ｑ∨Ｐ）　　８含意の定義
　　８（ア）　　　　　　　　（Ｑ＆～Ｐ）　　９ド・モルガンの法則
　　８（イ）　（Ｐ＆～Ｑ）∨（Ｑ＆～Ｐ）　　ア∨Ｉ
１　　（ウ）　（Ｐ＆～Ｑ）∨（Ｑ＆～Ｐ）　　１４７８イ∨Ｅ
（ⅱ）
１　　（１）　（Ｐ＆～Ｑ）∨（Ｑ＆～Ｐ）　　Ａ
　２　（２）　（Ｐ＆～Ｑ）　　　　　　　　　Ａ
　２　（３）～（～Ｐ∨Ｑ）　　　　　　　　　２ド・モルガンの法則
　２　（４）　～（Ｐ→Ｑ）　　　　　　　　　３含意の定義
　２　（５）　～（Ｐ→Ｑ）∨～（Ｑ→Ｐ）　　４∨Ｉ
　　６（６）　　　　　　　　（Ｑ＆～Ｐ）　　Ａ
　　６（７）　　　　　　　～（～Ｑ∨Ｐ）　　６ド・モルガンの法則
　　６（８）　　　　　　　　～（Ｑ→Ｐ）　　７含意の定義
　　６（９）　～（Ｐ→Ｑ）∨～（Ｑ→Ｐ）　　８∨Ｉ
１　　（ア）　～（Ｐ→Ｑ）∨～（Ｑ→Ｐ）　　１２５６９∨Ｅ
１　　（イ）～｛（Ｐ→Ｑ）＆　（Ｑ→Ｐ）｝　ア、ド・モルガンの法則
１　　（ウ）　～（Ｐ⇔Ｑ）　　　　　　　　　イＤｆ.⇔
従って、
（01）により、
（02）
① ～（Ｐ⇔ Ｑ）
② 　（Ｐ＆～Ｑ）∨（Ｑ＆～Ｐ）
に於いて、
①＝② である。
（03）
（ⅱ）
１　　（１）（Ｐ＆～Ｑ）∨（Ｑ＆～Ｐ）　Ａ
　２　（２）　Ｐ＆～Ｑ　　　　　　　　　Ａ
　２　（３）　Ｐ　　　　　　　　　　　　２＆Ｅ
　２　（４）　Ｐ∨　Ｑ　　　　　　　　　３∨Ｉ
　２　（５）　　　～Ｑ　　　　　　　　　２＆Ｅ
　２　（６）～Ｐ∨～Ｑ　　　　　　　　　５∨Ｉ
　２　（７）～（Ｐ＆Ｑ）　　　　　　　　６ド・モルガンの法則
　２　（８）　（Ｐ∨Ｑ）＆～（Ｐ＆Ｑ）　４７＆Ｉ
　　９（９）　　　　　　　（Ｑ＆～Ｐ）　Ａ
　　９（ア）　　　　　　　　Ｑ　　　　　９＆Ｅ
　　９（イ）　　　　　　Ｐ∨Ｑ　　　　　ア∨Ｉ
　　９（ウ）　　　　　　　　　　～Ｐ　　９＆Ｅ
　　９（エ）　　　　　　　～Ｐ∨～Ｑ　　ウ∨Ｉ
　　９（オ）　　　　　　　～（Ｐ＆Ｑ）　エ、ド・モルガンの法則
　　９（カ）　（Ｐ∨Ｑ）＆～（Ｐ＆Ｑ）　イオ＆Ｉ
１　　（キ）　（Ｐ∨Ｑ）＆～（Ｐ＆Ｑ）　１２８９カ∨Ｅ
（ⅲ）
１　　　　（１）　（Ｐ∨Ｑ）＆～（Ｐ＆Ｑ）　Ａ
１　　　　（２）　　Ｐ∨Ｑ　　　　　　　　　１＆Ｅ
１　　　　（３）　　　　　　　～（Ｐ＆Ｑ）　１＆Ｅ
　４　　　（４）　　　　　　　　　Ｐ　　　　Ａ
　　５　　（５）　　　　　　　　　　　Ｑ　　Ａ
　４５　　（６）　　　　　　　　　Ｐ＆Ｑ　　４５＆Ｉ
１４５　　（７）　～（Ｐ＆Ｑ）＆（Ｐ＆Ｑ）　３６＆Ｉ
１４　　　（８）　　　　　　　　　　～Ｑ　　５７ＲＡＡ
１　　　　（９）　　　　　　　　Ｐ→～Ｑ　　４８ＣＰ
　　　ア　（ア）　　Ｐ　　　　　　　　　　　Ａ
１　　ア　（イ）　　　　　　　　　　～Ｑ　　９アＭＰＰ
１　　ア　（ウ）　（Ｐ＆～Ｑ）　　　　　　　アイ＆Ｉ
１　　ア　（エ）（Ｐ＆～Ｑ）∨（Ｑ＆～Ｐ）　ウ∨Ｉ
　　　　オ（オ）　　　　Ｑ　　　　　　　　　Ａ
　　　　オ（カ）　　～～Ｑ　　　　　　　　　オＤＮ
１　　　オ（キ）　　　　　　　～Ｐ　　　　　９カＭＰＰ
１　　　オ（ク）　　　　Ｑ＆～Ｐ　　　　　　オキ＆Ｉ
１　　　オ（ケ）（Ｐ＆～Ｑ）∨（Ｑ＆～Ｐ）　ク∨Ｉ
１　　　　（コ）（Ｐ＆～Ｑ）∨（Ｑ＆～Ｐ）　１アエオケ∨Ｅ
従って、
（03）により、
（04）
②（Ｐ＆～Ｑ）∨（Ｑ＆～Ｐ）
③（Ｐ∨  Ｑ）＆～（Ｐ＆Ｑ）
に於いて、
②＝③ である。
（05）
（ⅲ）
１　　（１）　　（Ｐ∨　Ｑ）＆～（Ｐ＆Ｑ）　　Ａ
１　　（２）　　　Ｐ∨　Ｑ　　　　　　　　　　１＆Ｅ
１　　（３）～～（Ｐ∨　Ｑ）　　　　　　　　　２ＤＮ
１　　（４）～（～Ｐ＆～Ｑ）　　　　　　　　　３ド・モルガンの法則
　５　（５）　　～Ｐ　　　　　　　　　　　　　Ａ
　　６（６）　　　　　～Ｑ　　　　　　　　　　Ａ
　５６（７）　（～Ｐ＆～Ｑ）　　　　　　　　　５６＆Ｉ
１５６（８）～（～Ｐ＆～Ｑ）＆（～Ｐ＆～Ｑ）　３７＆Ｉ
１５　（９）　　　　～～Ｑ　　　　　　　　　　６８ＤＮ
１５　（ア）　　　　　　Ｑ　　　　　　　　　　９ＤＮ
１　　（イ）　　～Ｐ→　Ｑ　　　　　　　　　　５アＣＰ
１　　（ウ）　　　　　　　　　～（Ｐ＆Ｑ）　　１＆Ｅ
１　　（エ）　　　　　　　　　～Ｐ∨～Ｑ　　　ウ、ド・モルガンの法則
１　　（オ）　　　　　　　　　　Ｐ→～Ｑ　　　エ含意の定義
１　　（カ）　　（～Ｐ→Ｑ）＆（Ｐ→～Ｑ）　　イオ＆Ｉ
（ⅳ）
１　　（１）　　（～Ｐ→Ｑ）＆（Ｐ→～Ｑ）　　Ａ
１　　（２）　　　～Ｐ→Ｑ　　　　　　　　　　１＆Ｅ
１　　（３）　　～～Ｐ∨Ｑ　　　　　　　　　　２含意の定義
１　　（４）　　　　Ｐ∨Ｑ　　　　　　　　　　３ＤＮ
１　　（５）　　　　　　　　　　Ｐ→～Ｑ　　　１＆Ｅ
１　　（６）　　　　　　　　　～Ｐ∨～Ｑ　　　５含意の定義
１　　（７）　　　　　　　　～（Ｐ＆　Ｑ）　　６ド・モルガンの法則
１　　（８）　　　（Ｐ∨Ｑ）＆～（Ｐ＆Ｑ）　　４７＆Ｉ
従って、
（05）により、
（06）
③（Ｐ∨　Ｑ）＆～（Ｐ＆Ｑ）
④（～Ｐ→Ｑ）＆（Ｐ→～Ｑ）
に於いて、
③＝④ である。
従って、
（02）（04）（06）により、
（07）
① ～（Ｐ⇔　Ｑ）
②　 （Ｐ＆～Ｑ）∨（Ｑ＆～Ｐ）
③　 （Ｐ∨　Ｑ）＆～（Ｐ＆Ｑ）
④ 　（～Ｐ→Ｑ）＆（Ｐ→～Ｑ）
に於いて、すなはち、
①（ＰとＱの「真偽」が一致する）ことはない。
②（Ｐであって、Ｑでない）か、または（Ｑであって、Ｐでない）。
③（Ｐか、またはＱである）が、（Ｐであって、Ｑである）といふことはない。
④（ＰでないならばＱであり）、（Ｐであるならば、Ｑでない）。
に於いて、
①＝②＝③＝④である。
然るに、
（08）
日本語の接続詞「あるいは」には、両立的選言（弱選言）と排他的選言（強選言）の二つの意味があることに注意してほしい。

　― 中略 ―
論理学の「・・・あるいは・・・」は両立的選言に取り決めてある。それは論理学の体系がよりシンプルなものになるからである。
とりわけ、∨を両立的選言の方に決めておけば、
排他的選言の方は∨と＆と～によって簡単に表現できる―（Ｐ∨Ｑ）＆～（Ｐ＆Ｑ）―。
選言記号∨に対応する日本語には、「または」「もしくは」「・・・か・・・」などがある。
（昭和堂入門選書２５、論理学の基礎、1994年、１１頁改）
従って、
（07）（08）により、
（09）
① ～（Ｐ⇔　Ｑ）
②　 （Ｐ＆～Ｑ）∨（Ｑ＆～Ｐ）
③　 （Ｐ∨　Ｑ）＆～（Ｐ＆Ｑ）
④ 　（～Ｐ→Ｑ）＆（Ｐ→～Ｑ）
に於いて、すなはち、
①（ＰとＱの「真偽」が一致する）ことはない。
②（Ｐであって、Ｑでない）か、または（Ｑであって、Ｐでない）。
③（Ｐか、またはＱである）が、（Ｐであって、Ｑである）といふことはない。
④（ＰでないならばＱであり）、（Ｐであるならば、Ｑでない）。
に於いて、
① は「排他的選言（強選言）」であって、
② も「排他的選言（強選言）」であって、
③ も「排他的選言（強選言）」であって、
④ も「排他的選言（強選言）」である。
然るに、
（10）
「Ｐ∨Ｑ」は、「両立的選言（弱選言）」であって、
「Ｐ▽Ｑ」は、「排他的選言（強選言）」であるとする。
従って、
（09）（10）により、
（11）
（ⅰ）
１　（１）　　Ｐ▽Ｑ　　　　　　　　　Ａ
１　（２）（～Ｐ→Ｑ）＆（Ｐ→～Ｑ）　１Ｄｆ.▽
１　（３）　～Ｐ→Ｑ　　　　　　　　　２＆Ｅ
　２（４）　～Ｐ　　　　　　　　　　　Ａ
１２（５）　　　　Ｑ　　　　　　　　　３４ＭＰＰ
（ⅱ）
１　（１）　　Ｐ∨Ｑ　Ａ
１　（２）～～Ｐ∨Ｑ　１ＤＮ
１　（３）　～Ｐ→Ｑ　２含意の定義
　４（４）　～Ｐ　　　Ａ
１４（５）　　　　Ｑ　３４ＭＰＰ
従って、
（11）により、
（12）
① Ｐ▽Ｑ，～Ｐ├ Ｑ
② Ｐ∨Ｑ，～Ｐ├ Ｑ
といふ「推論」は、両方とも、「妥当」である。
然るに、
（13）
① Ｐ▽Ｑ，～Ｐ├ Ｑ
② Ｐ∨Ｑ，～Ｐ├ Ｑ
に於いて、
① は、「選言三段論法」であって、
② も、「選言三段論法」である。
従って、
（08）（09）（13）により、
（14）
①「（排他的）選言三段論法」は「妥当」であって、
②「（両立的）選言三段論法」も「妥当」である。
然るに、
（15）
日常的な言語では、「ＡまたはＢ」という言葉は、ＡとＢが両方真となる包含的論理和（inclusive disjunction, or）と、
いずれか一方が真でいずれか一方が偽となる排他的論理和（exclusive disjunction, xor）が区別されていないことがあります。
選言三段論法が妥当となるときは、後者、排他的論理和として「または」を使っているときに限られることがわかりますね。
（趣味の数学）
従って、、
（08）（15）により、
（16）
選言三段論法が妥当となるときは、後者、排他的論理和（選言）として「または」を使っているときに限られることがわかりますね。
といふ「説明」は、「マチガイ」である。
（17）
① ～（Ｐ⇔　Ｑ）
②　 （Ｐ＆～Ｑ）∨（Ｑ＆～Ｐ）
③　 （Ｐ∨　Ｑ）＆～（Ｐ＆Ｑ）
④ 　（～Ｐ→Ｑ）＆（Ｐ→～Ｑ）
に於いて、すなはち、
①（ＰとＱの「真偽」が一致する）ことはない。
②（Ｐであって、Ｑでない）か、または（Ｑであって、Ｐでない）。
③（Ｐか、またはＱである）が、（Ｐであって、Ｑである）といふことはない。
④（ＰでないならばＱであり）、（Ｐであるならば、Ｑでない）。
といふ「（４通リの）排他的選言（の定義）」に於いて、
① は「真理値表」を見れば、確かに、さうであって、「排他的選言」の「意味」からすれば、
② が「１番、分かり易い」ものの、「命題計算」の際には、
④ が「１番、扱い易い」。
令和０４年０７月２２日、毛利太。

「（ラッセルの）確定記述」の「例文」。

（01）
　　（22）∃ｘ｛（Ｉｘ＆Ｏｘ）＆∀ｙ（Ｉｙ→ｘ＝ｙ）｝
― ある人はイリアスを書いた、そしてオデュッセイアを書いた、そしてさらにその人はイリアスを書いたただ１人に人である。―
（E.J.レモン 著、竹尾治一郎・浅野楢英 訳、論理学初歩、1973年、１７７頁）
然るに、
（02）
（ⅰ）
１　（１）～∃ｘ｛（Ｉｘ＆Ｏｘ）＆　∀ｙ（Ｉｙ→ｘ＝ｙ）｝　Ａ
１　（２）∀ｘ～｛（Ｉｘ＆Ｏｘ）＆　∀ｙ（Ｉｙ→ｘ＝ｙ）｝　１量化子の関係
１　（３）　　～｛（Ｉａ＆Ｏａ）＆　∀ｙ（Ｉｙ→ａ＝ｙ）｝　１ＵＥ
１　（４）　　　～（Ｉａ＆Ｏａ）∨～∀ｙ（Ｉｙ→ａ＝ｙ）　　３ド・モルガンの法則
１　（５）　　　　（Ｉａ＆Ｏａ）→～∀ｙ（Ｉｙ→ａ＝ｙ）　　４含意の定義
　２（６）　　　　（Ｉａ＆Ｏａ）　　　　　　　　　　　　　　Ａ
１２（７）　　　　　　　　　　　　～∀ｙ（Ｉｙ→ａ＝ｙ）　　５６ＭＰＰ
１２（８）　　　　　　　　　　　　∃ｙ～（Ｉｙ→ａ＝ｙ）　　７量化子の関係
１２（９）　　　　　　　　　　　　　　～（Ｉｂ→ａ＝ｂ）　　Ａ
１２（ア）　　　　　　　　　　　　　～（～Ｉｂ∨ａ＝ｂ）　　９含意の定義
１２（イ）　　　　　　　　　　　　　　　　Ｉｂ＆ａ≠ｂ　　　アド・モルガンの法則
１２（ウ）　　　　　　　　　　　　　∃ｙ（Ｉｙ＆ａ≠ｙ）　　イＥＩ
１　（エ）　　　　（Ｉａ＆Ｏａ）→　∃ｙ（Ｉｙ＆ａ≠ｙ）　　２ウＣＰ
１　（オ）　∀ｘ｛（Ｉｘ＆Ｏｘ）→　∃ｙ（Ｉｙ＆ｘ≠ｙ）｝　エＵＩ
（ⅱ）
１　　（１）　∀ｘ｛（Ｉｘ＆Ｏｘ）→　∃ｙ（Ｉｙ＆ｘ≠ｙ）｝　Ａ
１　　（２）　　　　（Ｉａ＆Ｏａ）→　∃ｙ（Ｉｙ＆ａ≠ｙ）　　１ＵＥ
　３　（３）　　　　（Ｉａ＆Ｏａ）　　　　　　　　　　　　　　２３ＭＰＰ
１３　（４）　　　　　　　　　　　　　∃ｙ（Ｉｙ＆ａ≠ｙ）　　２３ＭＰＰ
１３　（５）　　　　　　　　　　　　　　　（Ｉｂ＆ａ≠ｂ）　　Ａ
　　６（６）　　　　　　　　　　　　　～（～Ｉｂ∨ａ≠ｂ）　　５ド・モルガンの法則
　　６（７）　　　　　　　　　　　　　　～（Ｉｂ→ａ≠ｂ）　　６含意の定義
　　６（８）　　　　　　　　　　　　∃ｙ～（Ｉｙ→ａ≠ｙ）　　７ＥＩ
１３　（９）　　　　　　　　　　　　∃ｙ～（Ｉｙ→ａ≠ｙ）　　５６８ＥＥ
１３　（ア）　　　　　　　　　　　　～∀ｙ（Ｉｙ→ａ≠ｙ）　　９量化子の関係
１　　（イ）　　　　（Ｉａ＆Ｏａ）→～∀ｙ（Ｉｙ→ａ≠ｙ）　　３アＣＰ
１　　（ウ）　　　～（Ｉａ＆Ｏａ）∨～∀ｙ（Ｉｙ→ａ＝ｙ）　　イ含意の定義
１　　（エ）　　～｛（Ｉａ＆Ｏａ）＆　∀ｙ（Ｉｙ→ａ＝ｙ）｝　ウ、ド・モルガンの法則
１　　（オ）∀ｘ～｛（Ｉｘ＆Ｏｘ）＆　∀ｙ（Ｉｙ→ｘ＝ｙ）｝　エＵＩ
１　　（カ）～∃ｘ｛（Ｉｘ＆Ｏｘ）＆　∀ｙ（Ｉｙ→ｘ＝ｙ）｝　オ量化子の関係
従って、
（02）により、
（03）
① 　∃ｘ｛（Ｉｘ＆Ｏｘ）＆∀ｙ（Ｉｙ→ｘ＝ｙ）｝
② ～∃ｘ｛（Ｉｘ＆Ｏｘ）＆∀ｙ（Ｉｙ→ｘ＝ｙ）｝
③ 　∀ｘ｛（Ｉｘ＆Ｏｘ）→∃ｙ（Ｉｙ＆ｘ≠ｙ）｝
に於いて、
② は、①の「否定」であって、
③＝② である。
従って、
（01）（02）（03）により、
（04）
① ∃ｘ｛（Ｉｘ＆Ｏｘ）＆∀ｙ（Ｉｙ→ｘ＝ｙ）｝
② ある人はイリアスを書いた、　そしてオデュッセイアを書いた、そしてさらにその人は、イリアスを書いたただ１人に人である。
③ ∀ｘ｛（Ｉｘ＆Ｏｘ）→∃ｙ（Ｉｙ＆ｘ≠ｙ）｝
④ いかなる人がイリアスを書き、そしてオデュッセイアを書いたとしても、その人以外にもイリアスを書いた人がゐる。
に於いて、
①＝② であって、
③＝④ であって、
③ は、①の「否定」である。
然るに、
（05）
ｈ＝ホメロス
であるとして、
１　（１）～∃ｘ｛（Ｉｘ＆Ｏｘ）＆　∀ｙ（Ｉｙ→ｘ＝ｙ）｝　Ａ
１　（２）∀ｘ～｛（Ｉｘ＆Ｏｘ）＆　∀ｙ（Ｉｙ→ｘ＝ｙ）｝　１量化子の関係
１　（３）　　～｛（Ｉｈ＆Ｏｈ）＆　∀ｙ（Ｉｙ→ｈ＝ｙ）｝　１ＵＥ
１　（４）　　　～（Ｉｈ＆Ｏｈ）∨～∀ｙ（Ｉｙ→ｈ＝ｙ）　　３ド・モルガンの法則
１　（５）　　　　（Ｉｈ＆Ｏｈ）→～∀ｙ（Ｉｙ→ｈ＝ｙ）　　４含意の定義
　２（６）　　　　（Ｉｈ＆Ｏｈ）　　　　　　　　　　　　　　Ａ
１２（７）　　　　　　　　　　　　～∀ｙ（Ｉｙ→ｈ＝ｙ）　　５６ＭＰＰ
１２（８）　　　　　　　　　　　　∃ｙ～（Ｉｙ→ｈ＝ｙ）　　７量化子の関係
１２（９）　　　　　　　　　　　　　　～（Ｉｂ→ｈ＝ｂ）　　Ａ
１２（ア）　　　　　　　　　　　　　～（～Ｉｂ∨ｈ＝ｂ）　　９含意の定義
１２（イ）　　　　　　　　　　　　　　　　Ｉｂ＆ｈ≠ｂ　　　アド・モルガンの法則
１２（ウ）　　　　　　　　　　　　　∃ｙ（Ｉｙ＆ｈ≠ｙ）　　イＥＩ
従って、
（05）により、
（06）
～∃ｘ｛（Ｉｘ＆Ｏｘ）＆∀ｙ（Ｉｙ→ｘ＝ｙ）｝，（Ｉｈ＆Ｏｈ）├ ∃ｙ（Ｉｙ＆ｈ≠ｙ）
といふ「推論」は、「妥当」である。
従って、
（04）（05）（06）により、
（07）
（ⅰ）いかなる人がイリアスを書き、そしてオデュッセイアを書いたとしても、その人以外にもイリアスを書いた人がゐる。然るに、
（ⅱ）ホメロスは、イリアスを書き、そしてオデュッセイアを書いた。従って、
（ⅲ）ホメロス以外にも、イリアスを書いた人がゐる。
といふ「推論」は、「妥当」である。
然るに、
（08）
（ⅰ）いかなる人がイリアスを書き、そしてオデュッセイアを書いたとしても、その人以外にもイリアスを書いた人がゐる。然るに、
（ⅱ）ホメロスは、イリアスを書き、そしてオデュッセイアを書いた。従って、
（ⅲ）ホメロス以外にも、イリアスを書いた人がゐる。
といふことは、「当然」であるため、その「意味」では、わざわざ、「述語論理」を学ぶ「必要」はない。
然るに、
（09）

従って、
（09）により、
（10）
フレーゲといふ数学者が、
∀ε∃δ∀ｘ（│ｘ－ａ│＜δ⊃│ｆ（ｘ）－ｆ（ａ）│＜ε）⇔
いかなるεであっても、そのεに対して、次のやうなδが存在する、すなはち、すべてのｘについて（│ｘ－ａ│＜δ⊃│ｆ（ｘ）－ｆ（ａ）│＜ε）といふ、そのやうなδが存在する。
といふことを、言ひたいがために、「述語論理」は「発明」された。
との、ことである。
従って、
（06）（10）により、
（11）
～∃ｘ｛（Ｉｘ＆Ｏｘ）＆∀ｙ（Ｉｙ→ｘ＝ｙ）｝
∀ε∃δ∀ｘ（│ｘ－ａ│＜δ⊃│ｆ（ｘ）－ｆ（ａ）│＜ε）
といふ「述語論理式」は、ある種の「数式」である（？）。
令和０４年０７月２１日、毛利太。

「天下英雄唯君与我」の「述語論理」（Ⅱ）。

（01）
１　　　　　　（１）∃ｘ∃ｙ｛（君ｘ＆英雄ｘ）＆（我ｙ＆英雄ｙ）＆（ｘ≠ｙ）＆∀ｚ［英雄ｚ→（ｚ＝ｘ）∨（ｚ＝ｙ）］｝　Ａ
　２　　　　　（２）　　∃ｙ｛（君ａ＆英雄ａ）＆（我ｙ＆英雄ｙ）＆（ａ≠ｙ）＆∀ｚ［英雄ｚ→（ｚ＝ａ）∨（ｚ＝ｙ）］｝　Ａ
　　３　　　　（３）　　　　　（君ａ＆英雄ａ）＆（我ｂ＆英雄ｂ）＆（ａ≠ｂ）＆∀ｚ［英雄ｚ→（ｚ＝ａ）∨（ｚ＝ｂ）　　　Ａ
　　３　　　　（４）　　　　　　君ａ　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　３＆Ｅ
　　３　　　　（５）　　　　　　　　　　　　　　　我ｂ　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　３＆Ｅ
　　３　　　　（６）　　　　　　　　　　　　　　　　　　　　　　　　　　　　　∀ｚ［英雄ｚ→（ｚ＝ａ）∨（ｚ＝ｂ）　　　３＆Ｅ
　　３　　　　（７）　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　英雄ｃ→（ｃ＝ａ）∨（ｃ＝ｂ）　　　６ＵＥ
　　　８　　　（８）　　∃ｚ（～君ｚ＆～我ｚ＆彼ｚ）　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　Ａ
　　　　９　　（９）　　　　　～君ｃ＆～我ｃ＆彼ｃ　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　Ａ
　　　　９　　（ア）　　　　　～君ｃ　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　９＆Ｅ
　　３　９　　（イ）　　　　　　君ａ＆～君ｃ　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　４ア＆Ｉ
　　　　　ウ　（ウ）　　　　　　　ｃ＝ａ　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　Ａ
　　３　９ウ　（エ）　　　　　　君ａ＆～君ａ　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　イウ＝Ｅ
　　３　９　　（オ）　　　　　　　ｃ≠ａ　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　ウエＲＡＡ
　　　　９　　（カ）　　　　　　　　　～我ｃ　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　９＆Ｅ
　　３　９　　（キ）　　　　　　　　　～我ｃ＆我ｂ　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　５カ＆Ｉ
　　　　　　ケ（ケ）　　　　　　　　　　　ｃ＝ｂ　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　Ａ
　　３　９　ケ（コ）　　　　　　　　　～我ｂ＆我ｂ　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　キケ＝Ｅ
　　３　９　　（サ）　　　　　　　　　　　ｃ≠ｂ　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　ケコＲＡＡ
　　３　９　　（シ）　　　　（ｃ≠ａ）＆（ｃ≠ｂ）　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　オサ＆Ｉ
　　３　９　　（ス）　　～｛（ｃ＝ａ）∨（ｃ＝ｂ）｝　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　シ、ド・モルガンの法則
　　３　９　　（セ）　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　～英雄ｃ　　　　　　　　　　　　　　　７スＭＴＴ
　　　　９　　（ソ）　　　　　　　　　　　　　彼ｃ　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　９＆Ｅ
　　３　９　　（タ）　　　　　　　　　　　　　彼ｃ＆～英雄ｃ　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　セソ＆Ｉ
　　３　９　　（チ）　　　　　　　　　　∃ｚ（彼ｚ＆～英雄ｚ）　　　　　　　　　　　　　　　　　　　　　　　　　　　　　タＥＩ
　　３８　　　（ツ）　　　　　　　　　　∃ｚ（彼ｚ＆～英雄ｚ）　　　　　　　　　　　　　　　　　　　　　　　　　　　　　８９チＥＥ
　２　８　　　（テ）　　　　　　　　　　∃ｚ（彼ｚ＆～英雄ｚ）　　　　　　　　　　　　　　　　　　　　　　　　　　　　　２３ツＥＥ
１　　８　　　（ト）　　　　　　　　　　∃ｚ（彼ｚ＆～英雄ｚ）　　　　　　　　　　　　　　　　　　　　　　　　　　　　　１２テＥＥ
従って、
（01）により、
（02）
（ⅰ）∃ｘ∃ｙ｛（君ｘ＆英雄ｘ）＆（我ｙ＆英雄ｙ）＆（ｘ≠ｙ）＆∀ｚ［英雄ｚ→（ｚ＝ｘ）∨（ｚ＝ｙ）］｝。然るに、
（ⅱ）　　∃ｚ（～君ｚ＆～我ｚ＆彼ｚ）。　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　従って、
（ⅲ）　　∃ｚ（彼ｚ＆～英雄ｚ）。
といふ「推論」、すなはち、
（ⅰ）あるｘとｙについて｛（ｘは君であって、ｘは英雄であって）、（ｙは我であって、ｙは英雄であって）、（ｘとｙは別人であって）、すべてのｚについて［ｚが英雄であるならば（ｚはｘであるか）、または（ｚはｙである）］｝。然るに、
（ⅱ）∃ｚについて（ｚは君ではなく、ｚは我ではなく、ｚは彼である）。従って、
（ⅲ）∃ｚについて（ｚは彼であって、ｚは英雄ではない）。
といふ「推論」は、「妥当」である。
従って、
（02）により、
（03）
（ⅰ）英雄唯君与我（英雄は君と私だけである）。　然るに、
（ⅱ）彼非君彼非我（彼は君ではなく私でもない）。従って、
（ⅲ）彼非英雄（彼は英雄ではない）。
といふ「推論」は、「述語論理」としても「妥当」である。
然るに、
（04）
人称代名詞（にんしょうだいめいし）とは、話し手、受け手、および談話の中で指定された人や物を指す代名詞である。
一般に、話し手を指す一人称、受け手を指す二人称、それ以外の人、物を指す三人称に分けられ、数が区別されることが多い。一部の言語では性も区別する。
（ウィキペディア）
従って、
（04）により、
（05）
「君・我・彼」は、普通は、「人称代名詞」である。
然るに、
（01）～（03）により、
（06）
∃ｘ∃ｙ｛（君ｘ＆英雄ｘ）＆（我ｙ＆英雄ｙ）＆（ｘ≠ｙ）＆∀ｚ［英雄ｚ→（ｚ＝ｘ）∨（ｚ＝ｙ）］｝，∃ｚ（～君ｚ＆～我ｚ＆彼ｚ）├ ∃ｚ（彼ｚ＆～英雄ｚ）
に於いて、
「君・我・彼」は、「述語文字」であって、
「ｘ・ｙ・ｚ」は、「変数」である。
然るに、
（07）
変数という記号を採用ることがいかに有効であるかは、進むにつれて次第に明らかになる。さしあたりそれは、代名詞「それ」（it）に似たようなはたらきをするものと考えれば十分であろう。
（E.J.レモン 著、竹尾治一郎・浅野楢英 訳、論理学初歩、1973年、１２１頁）
従って、
（06）（07）により、
（08）
∃ｘ∃ｙ｛（君ｘ＆英雄ｘ）＆（我ｙ＆英雄ｙ）＆（ｘ≠ｙ）＆∀ｚ［英雄ｚ→（ｚ＝ｘ）∨（ｚ＝ｙ）］｝
に於いては、
「ｘ・ｙ・ｚ（変数）」こそが、「代名詞（的）」であって、
「君・我・彼（述語）」に関しては、むしろ「普通名詞」である。
然るに、
（09）
「日本語に即した文法の樹立を」を目指すわれわれは「日本語で人称代名詞と呼ばれているものは、実は名詞だ」と宣言したい。どうしても区別したいなら「人称名詞」で十分だ。日本語の「人称代名詞」はこれからは「人称名詞」と呼ぼう（金谷武洋、日本語文法の謎を解く、2003年、４０・４１頁）。
従って、
（03）（08）（09）により、
（10）
「金谷武洋先生の説」に従ふならば、
（ⅰ）英雄唯君与我（英雄は君と私だけである）。　然るに、
（ⅱ）彼非君彼非我（彼は君ではなく私でもない）。従って、
（ⅲ）彼非英雄（彼は英雄ではない）。
に於ける「君・我・彼」は、「人称代名詞」ではなく「名詞」であって、
（ⅰ）∃ｘ∃ｙ｛（君ｘ＆英雄ｘ）＆（我ｙ＆英雄ｙ）＆（ｘ≠ｙ）＆∀ｚ［英雄ｚ→（ｚ＝ｘ）∨（ｚ＝ｙ）］｝。然るに、
（ⅱ）　　∃ｚ（～君ｚ＆～我ｚ＆彼ｚ）。　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　従って、
（ⅲ）　　∃ｚ（彼ｚ＆～英雄ｚ）。
に於ける「君・我・彼」も、「人称代名詞」ではなく「名詞」である。
といふ、ことになる。
令和０４年０７月２０日、毛利太。

「天下英雄唯君与我」の「述語論理」。

（01）
ｋ＝君
ｗ＝我
ｈ＝彼
であるとして、
１　　（１）英雄ｋ＆英雄ｗ＆∀ｘ｛英雄ｘ→（ｘ＝ｋ）∨（ｘ＝ｗ）｝　Ａ
１　　（２）英雄ｋ＆英雄ｗ　　　　　　　　　　　　　　　　　　　　　１＆Ｅ
１　　（３）　　　　　　　　∀ｘ｛英雄ｘ→（ｘ＝ｋ）∨（ｘ＝ｗ）｝　１＆Ｅ
１　　（４）　　　　　　　　　　　英雄ｈ→（ｈ＝ｋ）∨（ｈ＝ｗ）　　１ＵＥ
　５　（５）　　　　　　　　　　　　　　　（ｈ≠ｋ）＆（ｈ≠ｗ）　　Ａ
　５　（６）　　　　　　　　　　　　　～｛（ｈ＝ｋ）∨（ｈ＝ｗ）｝　６ド・モルガンの法則
１５　（７）　　　　　　　　　　～英雄ｈ　　　　　　　　　　　　　　４６ＭＴＴ
１　　（８）　　　　　　　　｛（ｈ≠ｋ）＆（ｈ≠ｗ）｝→～英雄ｈ　　５７ＣＰ
　　９（９）　　　　　　　　　（ｈ≠ｋ）＆（ｈ≠ｗ）　　　　　　　　Ａ
１　９（ア）　　　　　　　　　　　　　　　　　　　　　　～英雄ｈ　　８９ＭＰＰ
従って、
（01）により、
（02）
（ⅰ）英雄ｋ＆英雄ｗ＆∀ｘ｛英雄ｘ→（ｘ＝ｋ）∨（ｘ＝ｗ）｝。然るに、
（ⅱ）（ｈ≠ｋ）＆（ｈ≠ｗ）。従って、
（ⅲ）～英雄ｈ。
といふ「推論」、すなはち、
（ⅰ）君は英雄であり、私も英雄であり、すべてのｘについて｛ｘが英雄であるならば、（ｘは君である）か（ｘは私である）」。然るに、
（ⅱ）彼は君ではなく、彼は私でもない。従って、
（ⅲ）彼は英雄でない。
といふ「推論」は「妥当」である。
従って、
（01）（02）（03）により、
（04）
① ∀ｘ｛英雄ｘ→（ｘ＝ｋ）∨（ｘ＝ｗ）｝。
② 英雄唯君与我（英雄は、ただ君と我のみ）。
に於いて、
①＝② である。
然るに、
（05）
（ⅰ）
１　　　　（１）　∀ｘ｛英雄ｘ→（ｘ＝ｋ）∨（ｘ＝ｗ）｝　　Ａ
　２　　　（２）　∃ｘ（英雄ｘ＆（ｘ≠ｋ）＆（ｘ≠ｗ）｝　　Ａ
１　　　　（３）　　　　英雄ａ→（ａ＝ｋ）∨（ａ＝ｗ）　　　１ＵＥ
　　４　　（４）　　　　英雄ａ＆（ａ≠ｋ）＆（ａ≠ｗ）　　　Ａ
　　４　　（５）　　　　英雄ａ　　　　　　　　　　　　　　　４＆Ｅ
１　４　　（６）　　　　　　　　（ａ＝ｋ）∨（ａ＝ｗ）　　　３５ＭＰＰ
　　　７　（７）　　　　　　　　（ａ＝ｋ）　　　　　　　　　Ａ
　　４　　（８）　　　　　　　　（ａ≠ｋ）　　　　　　　　　４＆Ｅ
　　４７　（９）　　　　　　　　（ａ＝ｋ）＆（ａ≠ｋ）　　　７８＆Ｉ
　　　７　（ア）　　～｛英雄ａ＆（ａ≠ｋ）＆（ａ≠ｗ）｝　　４９ＲＡＡ
　　　　イ（イ）　　　　　　　　　　　　　　（ａ＝ｗ）　　　Ａ
　　４　　（ウ）　　　　　　　　　　　　　　（ａ≠ｗ）　　　４＆Ｅ
　　４　イ（エ）　　　　　　　　（ａ＝ｗ）＆（ａ≠ｗ）　　　イウ＆Ｉ
　　　　イ（オ）　　～｛英雄ａ＆（ａ≠ｋ）＆（ａ≠ｗ）｝　　４エＲＡＡ
１　４　　（カ）　　～｛英雄ａ＆（ａ≠ｋ）＆（ａ≠ｗ）｝　　６７アイオ∨Ｅ
１　４　　（キ）　　　｛英雄ａ＆（ａ≠ｋ）＆（ａ≠ｗ）｝＆
　　　　　　　　　　～｛英雄ａ＆（ａ≠ｋ）＆（ａ≠ｗ）｝　　４キ＆Ｉ
１２　　　（ク）　　　｛英雄ａ＆（ａ≠ｋ）＆（ａ≠ｗ）｝＆
　　　　　　　　　　～｛英雄ａ＆（ａ≠ｋ）＆（ａ≠ｗ）｝　　４キ＆Ｉ
１　　　　（ケ）～∃ｘ｛英雄ｘ＆（ｘ≠ｋ）＆（ｘ≠ｗ）｝　　２クＲＡＡ
（ⅲ）
１　（１）～∃ｘ（英雄ｘ＆（ｘ≠ｋ）＆（ｘ≠ｗ）｝　　Ａ
１　（２）∀ｘ～（英雄ｘ＆（ｘ≠ｋ）＆（ｘ≠ｗ）｝　　１量化子の関係
１　（３）　　～｛英雄ａ＆（ａ≠ｋ）＆（ａ≠ｗ）｝　　２ＵＥ
１　（４）　～｛英雄ａ＆［（ａ≠ｋ）＆（ａ≠ｗ）］｝　３結合法則
１　（５）　～英雄ａ∨～［（ａ≠ｋ）＆（ａ≠ｗ）］　　４ド・モルガンの法則
１　（６）　　英雄ａ→～［（ａ≠ｋ）＆（ａ≠ｗ）］　　５含意の定義
　７（７）　　英雄ａ　　　　　　　　　　　　　　　　　Ａ
１７（８）　　　　　　～［（ａ≠ｋ）＆（ａ≠ｗ）］　　６７ＭＰＰ
１７（９）　　　　　　　　（ａ＝ｋ）∨（ａ＝ｗ）　　　８ド・モルガンの法則
１　（ア）　　　　英雄ａ→（ａ＝ｋ）∨（ａ＝ｗ）　　　７９ＣＰ
１　（イ）　∀ｘ｛英雄ｘ→（ｘ＝ｋ）∨（ｘ＝ｗ）｝　　アＵＩ
従って、
（05）により、
（06）
① 　∀ｘ｛英雄ｘ→（ｘ＝ｋ）∨（ｘ＝ｗ）｝
③ ～∃ｘ｛英雄ｘ＆（ｘ≠ｋ）＆（ｘ≠ｗ）｝
に於いて、
①＝③ である。
従って、
（01）（04）（06）により、
（07）
① 　∀ｘ｛英雄ｘ→（ｘ＝ｋ）∨（ｘ＝ｗ）｝。
② 英雄唯君与我（英雄は、ただ君と我のみ）。
③ ～∃ｘ｛英雄ｘ＆（ｘ≠ｋ）＆（ｘ≠ｗ）｝。
④ 君ではなく、私でもない、英雄であるｘは存在しない。
に於いて、
①＝②＝③＝④ である。
令和０４年０７月１９日、毛利太。

「愛親者不敢惡於人」の「否定」の「述語論理」。

（01）
〔天子章第二〕
子曰、愛親者不敢惡於人。
子し曰く、親を愛する者は、敢へて人を悪まず。
（Ｗｅｂ漢文大系）
然るに、
（02）
① 愛親者不敢惡＿人。
② 愛親者不敢惡於人。
に於いて、
① ではなく、
② である以上、
① 敢へて人を悪ま＿ず（決して、人を憎ま＿ない）。
ではなく、
② 敢へて人を悪まれず（決して、人に憎まれない）。
であると、思はれる。
然るに、
（03）
∀ｘ∀ｙ｛（親ｘｙ＆愛ｙｘ）→～∃ｚ（人ｚ＆悪ｚｙ）｝⇔
すべてのｘとｙについて（ｘがｙの親であって、ｙがｘを愛するならば、あるｚについて（ｚが人であって、ｚがｙを悪む）といふことはない｝。
従って、
（02）（03）により、
（04）
愛親者不敢惡於人。⇔
愛（親）者不［敢惡〔於（人）〕］。⇔
（親）愛者［敢〔（人）於〕惡］不。⇔
親を愛する者は、敢へて人に惡まれず。⇔
∀ｘ∀ｙ｛（親ｘｙ＆愛ｙｘ）→～∃ｚ（人ｚ＆悪ｚｙ）｝⇔
すべてのｘとｙについて（ｘがｙの親であって、ｙがｘを愛するならば、あるｚについて（ｚが人であって、ｚがｙを悪む）といふことはない｝。
従って、
（04）により、
（05）
愛親者不必不敢惡於人。⇔
愛（親）者不｛必不［敢惡〔於（人）〕］｝。⇔
（親）愛者｛必［敢〔（人）於〕惡］不｝不。⇔
親を愛する者は、必ずしも敢へて人に悪まれずんばあらず。⇔
～∀ｘ∀ｙ｛（親ｘｙ＆愛ｙｘ）→～∃ｚ（人ｚ＆悪ｚｙ）｝⇔
すべてのｘとｙについて（ｘがｙの親であって、ｙがｘを愛するならば、あるｚについて（ｚが人であって、ｚがｙを悪む）といふことはない｝といふわけではない。
然るに、
（06）
（ⅰ）
１　　　（１）～∀ｘ∀ｙ｛（親ｘｙ＆愛ｙｘ）→～∃ｚ（人ｚ＆悪ｚｙ）｝　Ａ
１　　　（２）∃ｘ～∀ｙ｛（親ｘｙ＆愛ｙｘ）→～∃ｚ（人ｚ＆悪ｚｙ）｝　１量化子の関係
１　　　（３）∃ｘ∃ｙ～｛（親ｘｙ＆愛ｙｘ）→～∃ｚ（人ｚ＆悪ｚｙ）｝　２量化子の関係
　４　　（４）　　∃ｙ～｛（親ａｙ＆愛ｙａ）→～∃ｚ（人ｚ＆悪ｚｙ）｝　Ａ
　　５　（５）　　　　～｛（親ａｂ＆愛ｂａ）→～∃ｚ（人ｚ＆悪ｚｂ）｝　Ａ
　　５　（６）　　　～｛～（親ａｂ＆愛ｂａ）∨～∃ｚ（人ｚ＆悪ｚｂ）｝　５含意の定義
　　５　（７）　　　　　　（親ａｂ＆愛ｂａ）＆　∃ｚ（人ｚ＆悪ｚｂ）　　６ド・モルガンの法則
　　５　（８）　　　　　　（親ａｂ＆愛ｂａ）　　　　　　　　　　　　　　７＆Ｅ
　　５　（９）　　　　　　　　　　　　　　　　　∃ｚ（人ｚ＆悪ｚｂ）　　７＆Ｅ
　　　ア（ア）　　　　　　　　　　　　　　　　　　　（人ｃ＆悪ｃｂ）　　Ａ
　　５ア（イ）　　　　　　　　　（親ａｂ＆愛ｂａ）＆（人ｃ＆悪ｃｂ）　　８ア＆Ｉ
　　５ア（ウ）　　　　　　∃ｚ｛（親ａｂ＆愛ｂａ）＆（人ｚ＆悪ｚｂ）｝　イＥＩ
　　５　（エ）　　　　　　∃ｚ｛（親ａｂ＆愛ｂａ）＆（人ｚ＆悪ｚｂ）｝　５アウ
　　５　（オ）　　　　∃ｙ∃ｚ｛（親ａｙ＆愛ｙａ）＆（人ｚ＆悪ｚｙ）｝　エＥＩ
　４　　（カ）　　　　∃ｙ∃ｚ｛（親ａｙ＆愛ｙａ）＆（人ｚ＆悪ｚｙ）｝　４５オＥＩ
　４　　（キ）　　∃ｘ∃ｙ∃ｚ｛（親ｘｙ＆愛ｙｘ）＆（人ｚ＆悪ｚｙ）｝　カＥＩ
１　　　（ク）　　∃ｘ∃ｙ∃ｚ｛（親ｘｙ＆愛ｙｘ）＆（人ｚ＆悪ｚｙ）｝　１４キＥＥ
（ⅱ）
１　　　（１）　　∃ｘ∃ｙ∃ｚ｛（親ｘｙ＆愛ｙｘ）＆（人ｚ＆悪ｚｙ）｝　Ａ
　２　　（２）　　　　∃ｙ∃ｚ｛（親ａｙ＆愛ｙａ）＆（人ｚ＆悪ｚｙ）｝　Ａ
　　３　（３）　　　　　　∃ｚ｛（親ａｂ＆愛ｂａ）＆（人ｚ＆悪ｚｂ）｝　Ａ
　　　４（４）　　　　　　　　　（親ａｂ＆愛ｂａ）＆（人ｃ＆悪ｃｂ）　　Ａ
　　　４（５）　　　　　　　　　（親ａｂ＆愛ｂａ）　　　　　　　　　　　４＆Ｅ
　　　４（６）　　　　　　　　　　　　　　　　　　　（人ｃ＆悪ｃｂ）　　４＆Ｅ
　　　４（７）　　　　　　　　　　　　　　　　　∃ｚ（人ｚ＆悪ｚｂ）　　６ＥＩ
　　３　（８）　　　　　　　　　　　　　　　　　∃ｚ（人ｚ＆悪ｚｂ）　　３４７ＥＥ
　　３　（９）　　　　　　（親ａｂ＆愛ｂａ）＆　∃ｚ（人ｚ＆悪ｚｂ）　　４８＆Ｉ
　　３　（ア）　　　～｛～（親ａｂ＆愛ｂａ）∨～∃ｚ（人ｚ＆悪ｚｂ）｝　９ド・モルガンの法則
　　３　（イ）　　　　～｛（親ａｂ＆愛ｂａ）→～∃ｚ（人ｚ＆悪ｚｂ）｝　ア含意の定義
　　３　（ウ）　　∃ｙ～｛（親ａｙ＆愛ｙａ）→～∃ｚ（人ｚ＆悪ｚｙ）｝　イＥＩ
　２　　（エ）　　∃ｙ～｛（親ａｙ＆愛ｙａ）→～∃ｚ（人ｚ＆悪ｚｙ）｝　２３ウＥＥ
　２　　（オ）∃ｘ∃ｙ～｛（親ｘｙ＆愛ｙｘ）→～∃ｚ（人ｚ＆悪ｚｙ）｝　エＥＩ
１　　　（カ）∃ｘ∃ｙ～｛（親ｘｙ＆愛ｙｘ）→～∃ｚ（人ｚ＆悪ｚｙ）｝　１２オＥＥ
１　　　（キ）∃ｘ～∀ｙ｛（親ｘｙ＆愛ｙｘ）→～∃ｚ（人ｚ＆悪ｚｙ）｝　カ量化子の関係
１　　　（ク）～∀ｘ∀ｙ｛（親ｘｙ＆愛ｙｘ）→～∃ｚ（人ｚ＆悪ｚｙ）｝　キ量化子の関係
従って、
（06）により、
（07）
① ～∀ｘ∀ｙ｛（親ｘｙ＆愛ｙｘ）→～∃ｚ（人ｚ＆悪ｚｙ）｝
② ∃ｘ∃ｙ∃ｚ｛（親ｘｙ＆愛ｙｘ）＆　　（人ｚ＆悪ｚｙ）｝
に於いて、
①＝② である。
従って、
（05）（06）（07）により、
（08）
① 愛_レ親者不_三必不_二敢惡_一レ於_レ人。
② 親を愛する者は、必ずしも敢へて人に悪まれずんばあらず。
③ ∃ｘ∃ｙ∃ｚ｛（親ｘｙ＆愛ｙｘ）＆（人ｚ＆悪ｚｙ）｝。
④ あるｘとｙとｚについて｛ｘはｙの親であり、ｙはｘを愛し、ｚは人であって、ｚはｙを悪む｝。
に於いて、
①＝②＝③＝④ である。
従って、
（04）（08）により、
（09）
① 愛親者不敢惡於人。
② 愛親者不必不敢惡於人。
③ 　　∀ｘ∀ｙ｛（親ｘｙ＆愛ｙｘ）→～∃ｚ（人ｚ＆悪ｚｙ）｝。
④ ∃ｘ∃ｙ∃ｚ｛（親ｘｙ＆愛ｙｘ）＆（人ｚ＆悪ｚｙ）｝。
に於いて、
①＝③ であって、
②＝④ である。
然るに、
（10）
① ～∃ｚ（人ｚ＆悪ｚｙ）
② ～∃ｚ（人ｚ＆悪ｙｚ）
③ ｙを憎む人はゐない。
④ ｙは、人を憎まない。
に於いて、
①＝③ であって、
②＝④ である。
従って、
（01）（02）（10）により、
（11）
① 愛親者不敢惡於人（受動態）。
② 愛親者不敢惡＿人（能動態）。
であれば、「順番」に、
③ ∀ｘ∀ｙ｛（親ｘｙ＆愛ｙｘ）→～∃ｚ（人ｚ＆悪ｚｙ）｝。
④ ∀ｘ∀ｙ｛（親ｘｙ＆愛ｙｘ）→～∃ｚ（人ｚ＆悪ｙｚ）｝。
である。
令和０４年０７月１９日、毛利太。

「固有名（proper names）」を「述語文字」とした場合の「述語論理」。

―「昨日（令和０４年０７月１７日）の記事」の「（07）と（13）」だけを示した上で、「（14）～（19）」を「補足」します。―
従って、
（07）
１　　　　　　（１）∀ｘ（犯人ｘ→ｘ＝ｍ∨ｘ＝ｎ∨ｘ＝ｏ）　Ａ
　２　　　　　（２）∃ｘ（犯人ｘ＆現場ｘ）　　　　　　　　　Ａ
　　３　　　　（３）　～現場ｍ＆～現場ｎ　　　　　　　　　　Ａ
１　　　　　　（４）　　　犯人ａ→ａ＝ｍ∨ａ＝ｎ∨ａ＝ｏ　　１ＵＥ
　　　５　　　（５）　　　犯人ａ＆現場ａ　　　　　　　　　　Ａ
　　　５　　　（６）　　　犯人ａ　　　　　　　　　　　　　　５＆Ｅ
１　　５　　　（７）　　　　　　　ａ＝ｍ∨ａ＝ｎ∨ａ＝ｏ　　４６ＭＰＰ
１　　５　　　（８）　　　　　　ａ＝ｍ∨（ａ＝ｎ∨ａ＝ｏ）　７結合法則
１　　５　　　（９）　　　　　～ａ≠ｍ∨（ａ＝ｎ∨ａ＝ｏ）　８ＤＮ
１　　５　　　（ア）　　　　　　ａ≠ｍ→（ａ＝ｎ∨ａ＝ｏ）　９含意の定義
　　　　イ　　（イ）　　　　　　ａ≠ｍ　　　　　　　　　　　Ａ
１　　５イ　　（ウ）　　　　　　　　　　　ａ＝ｎ∨ａ＝ｏ　　アイＭＰＰ
１　　５イ　　（エ）　　　　　　　　　　～ａ≠ｎ∨ａ＝ｏ　　ウＤＮ
１　　５イ　　（オ）　　　　　　　　　　　ａ≠ｎ→ａ＝ｏ　　エ含意の定義
１　　５　　　（カ）　　　　　　ａ≠ｍ→（ａ≠ｎ→ａ＝ｏ）　イオＣＰ
　　３　　　　（キ）　　～現場ｍ　　　　　　　　　　　　　　３＆Ｅ
　　３　　　　（ク）　　　　　　～現場ｎ　　　　　　　　　　３＆Ｅ
　　　５　　　（ケ）　　　　　　　現場ａ　　　　　　　　　　５＆Ｅ
　　３５　　　（コ）　　～現場ｍ＆現場ａ　　　　　　　　　　キケ＆Ｉ
　　　　　サ　（サ）　　　　　ａ＝ｍ　　　　　　　　　　　　Ａ
　　３５　サ　（シ）　　～現場ｍ＆現場ｍ　　　　　　　　　　コサ＝Ｅ
　　３５　　　（ス）　　　　　ａ≠ｍ　　　　　　　　　　　　サシＲＡＡ
１　３５　　　（セ）　　　　　　　　　　　ａ≠ｎ→ａ＝ｏ　　カスＭＰＰ
　　３５　　　（ソ）　　～現場ｎ＆現場ａ　　　　　　　　　　クケ＆Ｉ
　　　　　　タ（タ）　　　　　ａ＝ｎ　　　　　　　　　　　　Ａ
　　３５　　タ（チ）　　～現場ｎ＆現場ｎ　　　　　　　　　　ソタ＝Ｅ８
　　３５　　　（ツ）　　　　　ａ≠ｎ　　　　　　　　　　　　タチＲＡＡ
１　３５　　　（テ）　　　　　　　　　　　　　　　ａ＝ｏ　　セツＭＰＰ
１　３５　　　（ト）　　　犯人ｏ　　　　　　　　　　　　　　６テ＝Ｅ
１２３　　　　（ナ）　　　犯人ｏ　　　　　　　　　　　　　　２５トＥＥ
に於いて、
　ｍ＝森山（といふ名前の個体）。
　ｎ＝中村（といふ名前の個体）。
　ｏ＝太田（といふ名前の個体）。
を用ひないのであれば、
森山＝森山である（といふ述語文字）。
中村＝中村である（といふ述語文字）。
太田＝太田である（といふ述語文字）。
を用ひることになる。
従って、
（13）
「１行目」は、
１（１）∀ｘ（犯人ｘ→ｘ＝ｍ∨ｘ＝ｎ∨ｘ＝ｏ）　Ａ
ではなく、
１（１）∀ｘ（犯人ｘ→森山ｘ∨中村ｘ∨太田ｘ）　Ａ
となるものの、「続きを書く」のは「疲れさう」なので「書きたくない」。
令和０４年０７月１７日、毛利太。
然るに、
（14）
「書きたくない」けれど、「書く」ことにすると、
１　　　　　　　　（１）　∀ｘ（犯人ｘ→森山ｘ∨中村ｘ∨太田ｘ）　Ａ
　２　　　　　　　（２）　∃ｘ（犯人ｘ＆　現場ｘ）　　　　　　　　Ａ
　　３　　　　　　（３）　∃ｘ（森山ｘ＆～現場ｘ）　　　　　　　　Ａ
　　　４　　　　　（４）　∃ｘ（中村ｘ＆～現場ｘ）　　　　　　　　Ａ
１　　　　　　　　（５）　　　　犯人ａ→森山ａ∨中村ａ∨太田ａ　　１ＵＥ
　　　　６　　　　（６）　　　　犯人ａ＆　現場ａ　　　　　　　　　Ａ
　　　　　７　　　（７）　　　　森山ａ＆～現場ａ　　　　　　　　　Ａ
　　　　　　８　　（８）　　　　中村ａ＆～現場ａ　　　　　　　　　Ａ
　　　　６　　　　（９）　　　　犯人ａ　　　　　　　　　　　　　　６＆Ｅ
１　　　６　　　　（ア）　　　　　　　　森山ａ∨中村ａ∨太田ａ　　５９ＭＰＰ
１　　　６　　　　（イ）　　　　　　　森山ａ∨（中村ａ∨太田ａ）　ア結合法則
１　　　６　　　　（ウ）　　　　　～～森山ａ∨（中村ａ∨太田ａ）　イＤＮ
１　　　６　　　　（エ）　　　　　　～森山ａ→（中村ａ∨太田ａ）　ウ含意の定義
　　　　６　　　　（オ）　　　　　　　　　現場ａ　　　　　　　　　６＆Ｅ
　　　　　７　　　（カ）　　　　　　　　～現場ａ　　　　　　　　　７＆Ｅ
　　　　　　８　　（キ）　　　　　　　　～現場ａ　　　　　　　　　８＆Ｅ
　　　　６７　　　（ク）　　　　現場ａ＆～現場ａ　　　　　　　　　オカ＆Ｉ
　　　　６　　　　（ケ）　　～（森山ａ＆～現場ａ）　　　　　　　　７クＲＡＡ
　　　　６　　　　（コ）　　　～森山ａ∨　現場ａ　　　　　　　　　ケ、ド・モルガンの法則
　　　　６　　　　（サ）　　　　森山ａ→　現場ａ　　　　　　　　　ケ、含意の定義
　　　　　　　シ　（シ）　　　　森山ａ　　　　　　　　　　　　　　Ａ
　　　　６　　シ　（ス）　　　　　　　　　現場ａ　　　　　　　　　サシＭＰＰ
　　　　６７　シ　（セ）　　　　　～現場＆現場ａ　　　　　　　　　カス＆Ｉ
　　　　６７　　　（ソ）　　　～森山ａ　　　　　　　　　　　　　　シセＲＡＡ
　　３　６　　　　（タ）　　　～森山ａ　　　　　　　　　　　　　　３７ソＥＥ
１　３　６　　　　（チ）　　　　　　　　　　　　中村ａ∨太田ａ　　エタＭＰＰ
１　３　６　　　　（ツ）　　　　　　　　　　～～中村ａ∨太田ａ　　チＤＮ
１　３　６　　　　（テ）　　　　　　　　　　　～中村ａ→太田ａ　　ツ含意の定義
　　　　　　８　　（ト）　　　　　　　　～現場ａ　　　　　　　　　８＆Ｅ
　　　　６　８　　（ナ）　　　　　～現場＆現場ａ　　　　　　　　　オト＆Ｉ
　　　　６　　　　（ニ）　　～（中村ａ＆～現場ａ）　　　　　　　　８ナＲＡＡ
　　　　６　　　　（ヌ）　　　～中村ａ∨　現場ａ　　　　　　　　　ニ、ド・モルガンの法則
　　　　６　　　　（ネ）　　　　中村ａ→　現場ａ　　　　　　　　　ヌ、含意の定義
　　　　　　　　ノ（ノ）　　　　中村ａ　　　　　　　　　　　　　　Ａ
　　　　６　　　ノ（ハ）　　　　　　　　　現場ａ　　　　　　　　　ネノＭＰＰ
　　　　６　８　ノ（ヒ）　　　　～現場ａ＆現場ａ　　　　　　　　　キハ＆Ｉ
　　　　６　８　　（フ）　　　～中村ａ　　　　　　　　　　　　　　ノヒＲＡＡ
　　　４６　　　　（ヘ）　　　～中村ａ　　　　　　　　　　　　　　４８フＥＥ
１　３４６　　　　（ホ）　　　　　　　　　　　　　　　　太田ａ　　テヘＭＰＰ
１　３４６　　　　（マ）　　　　犯人ａ＆太田ａ　　　　　　　　　　９ホ＆Ｅ
１　３４６　　　　（ミ）　∃ｘ（犯人ｘ＆太田ｘ）　　　　　　　　　マＥＩ
１２３４　　　　　（ム）　∃ｘ（犯人ｘ＆太田ｘ）　　　　　　　　　２６ミＥＥ
従って、
（14）により、
（15）
∀ｘ（犯人ｘ→森山ｘ∨中村ｘ∨太田ｘ），∃ｘ（犯人ｘ＆現場ｘ），∃ｘ（森山ｘ＆～現場ｘ），∃ｘ（中村ｘ＆～現場ｘ）├ ∃ｘ（犯人ｘ＆太田ｘ）
といふ「連式」、すなはち、
（ⅰ）∀ｘ（犯人ｘ→森山ｘ∨中村ｘ∨太田ｘ）。然るに、
（ⅱ）∃ｘ（犯人ｘ＆　現場ｘ）。然るに、<ｂｒ> （ⅲ）∃ｘ（森山ｘ＆～現場ｘ）。然るに、
（ⅳ）∃ｘ（中村ｘ＆～現場ｘ）。従って、
（ⅴ）∃ｘ（犯人ｘ＆太田ｘ）。
といふ「推論」は、「述語論理」として「妥当」である。
従って、
（16）
（ⅰ）すべてのｘについて（ｘが犯人であるならば、ｘは森山か、ｘは中村か、ｘは太田である）。然るに、
（ⅱ）　　あるｘについて（ｘは犯人であって、ｘは現場にゐた）。　　　然るに、
（ⅲ）　　あるｘについて（ｘは森山であって、ｘは現場にゐなかった）。然るに、
（ⅳ）　　あるｘについて（ｘは中村であって、ｘは現場にゐなかった）。従って、
（ⅴ）　　あるｘについて（ｘは犯人であって、ｘは太田である）。
といふ「推論」は、「述語論理」として「妥当」である。
従って、
（16）により、
（17）
（ⅰ）犯人は、森山か、中村か、太田である。然るに、
（ⅱ）犯人は、現場にゐた。　　　　　　　　然るに、
（ⅲ）森山にはアリバイがある。　　　　　　然るに、
（ⅳ）中村にもアリバイがある。　　　　　　従って、
（ⅴ）太田が犯人である（犯人は太田である）。
といふ「推論」は、「日本語」としても、「述語論理」としても「妥当」である。
従って、
（11）～（17）により、
（18）
① ∀ｘ（犯人ｘ→ｘ＝ｍ∨ｘ＝ｎ∨ｘ＝ｏ），∃ｘ（犯人ｘ＆現場ｘ），～現場ｍ＆～現場ｎ├ 犯人ｏ
② ∀ｘ（犯人ｘ→森山ｘ∨中村ｘ∨太田ｘ），∃ｘ（犯人ｘ＆現場ｘ），∃ｘ（森山ｘ＆～現場ｘ），∃ｘ（中村ｘ＆～現場ｘ）├ ∃ｘ（犯人ｘ＆太田ｘ）
に於ける、
① のやうに、
　ｍ＝森山（といふ名前の個体）。
　ｎ＝中村（といふ名前の個体）。
　ｏ＝太田（といふ名前の個体）。
を用ひたとしても、
② のように、
森山＝森山である（といふ述語文字）。
中村＝中村である（といふ述語文字）。
太田＝太田である（といふ述語文字）。
を用ひたとしても、
（ⅰ）犯人は、森山か、中村か、太田である。然るに、
（ⅱ）犯人は、現場にゐた。　　　　　　　　然るに、
（ⅲ）森山と中村には、アリバイがある。　　従って、
（ⅳ）太田が犯人である。
といふ「推論」は、「述語論理」として、「妥当」である。
然るに、
（19）
① ∀ｘ（犯人ｘ→ｘ＝ｍ∨ｘ＝ｎ∨ｘ＝ｏ），∃ｘ（犯人ｘ＆現場ｘ），～現場ｍ＆～現場ｎ├ 犯人ｏ
② ∀ｘ（犯人ｘ→森山ｘ∨中村ｘ∨太田ｘ），∃ｘ（犯人ｘ＆現場ｘ），∃ｘ（森山ｘ＆～現場ｘ），∃ｘ（中村ｘ＆～現場ｘ）├ ∃ｘ（犯人ｘ＆太田ｘ）
に於いて、
① の「証明」を書く方が、
② の「証明」を書くよりも、「簡単」である。
令和０４年０７月１８日、毛利太。

「京大（を含む世間一般）の述語論理」には「任意の名前」が無い。

（01）
第一に、固有名（proper name）をつぎの符号のひとつとして定義する。
　　　ｍ，ｎ，・・・・・・
第二に、任意の名前（aribitary name）をつぎの符号のひとつとして定義する。
　　　ａ，ｂ，ｃ，・・・・・・
第三に、個体変数（individual variable）をつぎの符号のひとつとして定義する。
　　　ｘ，ｙ，ｚ，・・・・・・
第四に、述語文字（predicate-letter）をつぎの符号のひとつとして定義する。
（E.J.レモン 著、竹尾治一郎・浅野楢英 訳、論理学初歩、1973年、１７６頁）
（02）
固有名と任意の名前をいずれかを包括する語を導入しておくのが便利なことは明らかである。
それ故、ターム（term）を、固有名あるいは任意の名前と定義する。
（E.J.レモン 著、竹尾治一郎・浅野楢英 訳、論理学初歩、1973年、１７７頁改）
従って、
（01）（02）により、
（03）
「E.J.レモンの述語論理」には、
「固有名（proper name）」といふ「ターム（term）」と、
「任意の名前（aribitary name）」といふ「ターム（term）」による、
「２種類のターム（term）」がある。
然るに、
（04）

従って、
（04）により、
（05）
「京大（大西琢朗先生）の述語論理」では、
「個体変項（individual variables）」と、
「個体定項（individual constants）」とを、「ターム（term）」と呼ぶ。
従って、
（01）～（05）により、
（06）
「（京大を含む）世間一般の述語論理」には、どうやら、
「E.J.レモンの述語論理」には有る所の、
「固有名（proper name）」と、
「任意の名前（aribitary name）」の「区別」が無いやうである。
然るに、
（07）
昨日も示したものの、
　ｍ＝森山（といふ名前の個体）。
　ｎ＝中村（といふ名前の個体）。
　ｏ＝太田（といふ名前の個体）。
犯人＝犯人である（といふ述語文字）。
現場＝現場にゐた（といふ述語文字）。
であるとして、
１　　　　　　（１）∀ｘ（犯人ｘ→ｘ＝ｍ∨ｘ＝ｎ∨ｘ＝ｏ）　Ａ
　２　　　　　（２）∃ｘ（犯人ｘ＆現場ｘ）　　　　　　　　　Ａ
　　３　　　　（３）　～現場ｍ＆～現場ｎ　　　　　　　　　　Ａ
１　　　　　　（４）　　　犯人ａ→ａ＝ｍ∨ａ＝ｎ∨ａ＝ｏ　　１ＵＥ
　　　５　　　（５）　　　犯人ａ＆現場ａ　　　　　　　　　　Ａ
　　　５　　　（６）　　　犯人ａ　　　　　　　　　　　　　　５＆Ｅ
１　　５　　　（７）　　　　　　　ａ＝ｍ∨ａ＝ｎ∨ａ＝ｏ　　４６ＭＰＰ
１　　５　　　（８）　　　　　　ａ＝ｍ∨（ａ＝ｎ∨ａ＝ｏ）　７結合法則
１　　５　　　（９）　　　　　～ａ≠ｍ∨（ａ＝ｎ∨ａ＝ｏ）　８ＤＮ
１　　５　　　（ア）　　　　　　ａ≠ｍ→（ａ＝ｎ∨ａ＝ｏ）　９含意の定義
　　　　イ　　（イ）　　　　　　ａ≠ｍ　　　　　　　　　　　Ａ
１　　５イ　　（ウ）　　　　　　　　　　　ａ＝ｎ∨ａ＝ｏ　　アイＭＰＰ
１　　５イ　　（エ）　　　　　　　　　　～ａ≠ｎ∨ａ＝ｏ　　ウＤＮ
１　　５イ　　（オ）　　　　　　　　　　　ａ≠ｎ→ａ＝ｏ　　エ含意の定義
１　　５　　　（カ）　　　　　　ａ≠ｍ→（ａ≠ｎ→ａ＝ｏ）　イオＣＰ
　　３　　　　（キ）　　～現場ｍ　　　　　　　　　　　　　　３＆Ｅ
　　３　　　　（ク）　　　　　　～現場ｎ　　　　　　　　　　３＆Ｅ
　　　５　　　（ケ）　　　　　　　現場ａ　　　　　　　　　　５＆Ｅ
　　３５　　　（コ）　　～現場ｍ＆現場ａ　　　　　　　　　　キケ＆Ｉ
　　　　　サ　（サ）　　　　　ａ＝ｍ　　　　　　　　　　　　Ａ
　　３５　サ　（シ）　　～現場ｍ＆現場ｍ　　　　　　　　　　コサ＝Ｅ
　　３５　　　（ス）　　　　　ａ≠ｍ　　　　　　　　　　　　サシＲＡＡ
１　３５　　　（セ）　　　　　　　　　　　ａ≠ｎ→ａ＝ｏ　　カスＭＰＰ
　　３５　　　（ソ）　　～現場ｎ＆現場ａ　　　　　　　　　　クケ＆Ｉ
　　　　　　タ（タ）　　　　　ａ＝ｎ　　　　　　　　　　　　Ａ
　　３５　　タ（チ）　　～現場ｎ＆現場ｎ　　　　　　　　　　ソタ＝Ｅ８
　　３５　　　（ツ）　　　　　ａ≠ｎ　　　　　　　　　　　　タチＲＡＡ
１　３５　　　（テ）　　　　　　　　　　　　　　　ａ＝ｏ　　セツＭＰＰ
１　３５　　　（ト）　　　犯人ｏ　　　　　　　　　　　　　　６テ＝Ｅ
１２３　　　　（ナ）　　　犯人ｏ　　　　　　　　　　　　　　２５トＥＥ
といふ「述語計算（Predicate calculus）」は「正しい」。
従って、
（01）（07）により、
（08）
∀ｘ（犯人ｘ→ｘ＝ｍ∨ｘ＝ｎ∨ｘ＝ｏ），∃ｘ（犯人ｘ＆現場ｘ），～現場ｍ＆～現場ｎ├ 犯人ｏ
といふ「連式」、すなはち、
（ⅰ）∀ｘ（犯人ｘ→ｘ＝ｍ∨ｘ＝ｎ∨ｘ＝ｏ）。然るに、
（ⅱ）∃ｘ（犯人ｘ＆現場ｘ）。　　　　　　　　然るに、
（ⅲ）　～現場ｍ＆～現場ｎ。　　　　　　　　　従って、
（ⅳ）　　　犯人ｏ。
といふ「推論」は、「E.J.レモンの述語論理」として「妥当」である。
従って、
（08）により、
（09）
（ⅰ）すべてのｘについて（ｘが犯人であるならば、ｘはｍか、ｘはｎか、ｏである。 然るに、
（ⅱ）　　あるｘについて（ｘは犯人であって、ｘは現場にゐた）。　　　　　　　　 然るに、
（ⅲ）ｍは現場にゐなかったし、ｎも現場にゐなかった。　　　　　　　　　　　　　 従って、
（ⅳ）ｏが犯人である（犯人はｏである）。
といふ「推論」は、「妥当」である。
といふ「推論」は、「E.J.レモンの述語論理」として「妥当」である。
従って、
（09）により、
（10）
（ⅰ）犯人は、森山か、中村か、太田である。然るに、
（ⅱ）犯人は、現場にゐた。　　　　　　　　然るに、
（ⅲ）森山と中村には、アリバイがある。　　従って、
（ⅳ）太田が犯人である。
といふ「推論」は、「E.J.レモンの述語論理」としては「妥当」である。
従って、
（06）～（10）により、
（11）
（ⅰ）犯人は、森山か、中村か、太田である。然るに、
（ⅱ）犯人は、現場にゐた。　　　　　　　　然るに、
（ⅲ）森山と中村には、アリバイがある。　　従って、
（ⅳ）太田が犯人である。
といふ「推論」は、「（京大を含む）世間一般の述語論理」としても「妥当」であるか「否」かは、「現時点での私」には、分からない。
（12）
　ｍ＝森山（といふ名前の個体）。
　ｎ＝中村（といふ名前の個体）。
　ｏ＝太田（といふ名前の個体）。
を用ひないのであれば、
森山＝森山である（といふ述語文字）。
中村＝中村である（といふ述語文字）。
太田＝太田である（といふ述語文字）。
を用ひることになる。
従って、
（13）
「１行目」は、
１（１）∀ｘ（犯人ｘ→ｘ＝ｍ∨ｘ＝ｎ∨ｘ＝ｏ）　Ａ
ではなく、
１（１）∀ｘ（犯人ｘ→森山ｘ∨中村ｘ∨太田ｘ）　Ａ
となるものの、「続きを書く」のは「難しさう」なので「書きたくない」。
令和０４年０７月１７日、毛利太。

「多くとも一人（at most one）」の「述語論理」。

（01）
２ つぎの論証を等号を含む述語計算の記号に翻訳し、それに対応うる連式の妥当性を示すことによって、論証の健全性を証明せよ。
（ｄ）多くとも１人（at most one）の無法な国家主席がいる。毛沢東は無法な国家主席である。ジョンソンは毛沢東ではない。故にジョンソンは無法な国家主席ではない。
（E.J.レモン 著、竹尾治一郎・浅野楢英 訳、論理学初歩、1973年、２１５頁）
然るに、
（02）
Ｆ＝無法な国家主席である（といふ述語文字）。
ｊ＝ジョンソン（といふ名前の個人）。
ｍ＝毛沢東（といふ名前の個人）。
とする。
然るに、
（03）
① ∃ｘ∃ｙ（Ｆｘ＆Ｆｙ＆ｘ≠ｙ）。
② 少なくとも、２人以上のＦがゐる。
③ あるｘとｙについて（ｘはＦであり、ｙもＦであり、ｘとｙは同じではない）。
に於いて、
①＝②＝③ である。
従って、
（03）により、
（04）
① ～∃ｘ∃ｙ（Ｆｘ＆Ｆｙ＆ｘ≠ｙ）。
② Ｆは０人か、または、Ｆは１人である。
③ 多くとも１人のＦがゐる（０人か１人がＦである）。
に於いて、
①＝②＝③ である。
然るに、
（05）
１　　（１）～∃ｘ∃ｙ（Ｆｘ＆Ｆｙ＆ｘ≠ｙ）　Ａ
１　　（２）∀ｘ～∃ｙ（Ｆｘ＆Ｆｙ＆ｘ≠ｙ）　１量化子の関係
１　　（３）∀ｘ∀ｙ～（Ｆｘ＆Ｆｙ＆ｘ≠ｙ）　２量化子の関係
１　　（４）　　∀ｙ～（Ｆｍ＆Ｆｙ＆ｍ≠ｙ）　３ＵＥ
１　　（５）　　　　～（Ｆｍ＆Ｆｊ＆ｍ≠ｊ）　４ＵＥ
１　　（６）　　～｛（Ｆｍ＆Ｆｊ）＆ｍ≠ｊ｝　５結合法則
１　　（７）　　　～（Ｆｍ＆Ｆｊ）∨ｍ＝ｊ　　６ド・モルガンの法則
１　　（８）　　　　（Ｆｍ＆Ｆｊ）→ｍ＝ｊ　　７含意の定義
　９　（９）　　　　　Ｆｍ　　　　　　　　　　Ａ
　　ア（ア）　　　　　　　　　　　　ｍ≠ｊ　　Ａ
１　ア（イ）　　　～（Ｆｍ＆Ｆｊ）　　　　　　８アＭＴＴ
１　ア（ウ）　　　～Ｆｍ∨～Ｆｊ　　　　　　　イ、ド・モルガンの法則
１　ア（エ）　　　　Ｆｍ→～Ｆｊ　　　　　　　ウ含意の定義
１９ア（オ）　　　　　　　～Ｆｊ　　　　　　　９エＭＰＰ
従って、
（05）により、
（06）
（ⅰ）～∃ｘ∃ｙ（Ｆｘ＆Ｆｙ＆ｘ≠ｙ）。然るに、
（ⅱ）　Ｆｍ。　　　　　　　　　　　　　故に、
（ⅲ）～Ｆｊ。
といふ「推論」は「妥当」である。
従って、
（01）～（05）により、
（06）
（ⅰ）「無法な国家主席は、多くとも一人（at most one）しかゐない。」然るに、
（ⅱ）「毛沢東は無法な国家主席である。」従って、
（ⅲ）「ジョンソンは無法な国家主席ではない。」
といふ「推論」は、「日本語」としてだけでなく、「述語論理」としても、「妥当」である。
令和０４年０７月１７日、毛利太。

「述語論理の定数（固有名）」について。

（01）
ｙ＝１ｘ＋２
ｙ＝２ｘ＋３
ｙ＝３ｘ＋４
ｙ＝４ｘ＋５
ｙ＝５ｘ＋６
・・・・・・
と書く「代り」に、「ひとまとめ」にして、
ｙ＝ａｘ＋ｂ
といふ風に書く。
従って、
（01）により、
（02）
２ｘ＝ｙ－３
ａｘ＝ｙ－ｂ
に於いて、
２は、「定数」であって、
ｘは、「変数」であって、
ａも、「定数」であるが、
ａは、「任意の定数」である。
然るに、
（03）
第一に、固有名詞（proper name）をつぎの符号のひとつとして定義する。
　　　ｍ，ｎ，・・・・・・
第二に、任意の名前（aribitary name）をつぎの符号のひとつとして定義する。
　　　ａ，ｂ，ｃ，・・・・・・
第三に、個体変数（individual variable）をつぎの符号のひとつとして定義する。
　　　ｘ，ｙ，ｚ，・・・・・・
第四に、述語文字（predicate-letter）をつぎの符号のひとつとして定義する。
（E.J.レモン 著、竹尾治一郎・浅野楢英 訳、論理学初歩、1973年、１７６頁）
然るに、
（04）
１００ Ｆｍ，∀ｘ（Ｆｘ→Ｇｘ）├ Ｇｍ
１　（１）　　　Ｆｍ　　　　　Ａ
　２（２）∀ｘ（Ｆｘ→Ｇｘ）　Ａ
　２（３）　　　Ｆｍ→Ｇｍ　　２ＵＥ
１２（４）　　　　　　Ｇｍ　　１３ＭＰＰ
１００は論理学では有名なつぎの論証に見られるような、明らかに健全な論証の形式を示している。
（３）ソクラテスは人間（ａ ｍａｎ）である。すべての人間（ａｌｌ ｍｅｎ）は死すべきもの（ｍｏｒｔａｌ）である。故にソクラテスは死すべきものである。
（E.J.レモン 著、竹尾治一郎・浅野楢英 訳、論理学初歩、1973年、１３４頁改）
従って、
（01）～（04）により、
（05）
「話の世界」＝「自然数の集合」
とするならば、
第一に、固有名詞（proper name）をつぎの符号のひとつとして定義する。
　　　ｍ，ｎ，ｏ，・・・・・・
といふ「それ」は、
　　　１，２，３，・・・・・・
であって、
「話の世界」＝「哲学者の集合」
とするならば、
第一に、固有名詞（proper name）をつぎの符号のひとつとして定義する。
　　　ｍ，ｎ，ｏ，・・・・・・
といふ「それ」は、
　　　プラトン、ソクラテス、アリストテレス，・・・・・・
である。
従って、
（05）により、
（06）
ｍ＝森山
ｎ＝中村
ｏ＝太田
であるならば、
ｍ＝森山といふ「個人」を示す「名前」であって、
ｎ＝中村といふ「個人」を示す「名前」であって、
ｏ＝太田といふ「個人」を示す「名前」である。
従って、
（05）（06）により、
（07）
第一に、固有名詞（proper name）をつぎの符号のひとつとして定義する。
　　　ｍ，ｎ，ｏ，・・・・・・
といふ場合は、「話の世界」に応じて、
ｍ＝１
ｎ＝２
ｏ＝３
であっても、構わないし、
ｍ＝森山
ｎ＝中村
ｏ＝太田
であっても、構はない。
然るに、
（08）
１　　　　　（１）∀ｘ（犯人ｘ→ｘ＝ｍ∨ｘ＝ｎ∨ｘ＝ｏ）　Ａ
　２　　　　（２）∃ｘ（犯人ｘ＆現場ｘ）　　　　　　　　　Ａ
１　　　　　（３）　　　犯人ａ→ａ＝ｍ∨ａ＝ｎ∨ａ＝ｏ　　１ＵＥ
　　４　　　（４）　　　犯人ａ＆現場ａ　　　　　　　　　　Ａ
　　４　　　（５）　　　犯人ａ　　　　　　　　　　　　　　４＆Ｅ
　　４　　　（６）　　　　　　　現場ａ　　　　　　　　　　４＆Ｅ
　　　７　　（７）　　　　　　～現場ｍ＆～現場ｎ　　　　　Ａ
　　　７　　（８）　　　　　　～現場ｍ　　　　　　　　　　７＆Ｅ
　　　７　　（９）　　　　　　　　　　　～現場ｎ　　　　　７＆Ｅ
１　４　　　（ア）　　　　　　　ａ＝ｍ∨ａ＝ｎ∨ａ＝ｏ　　３５ＭＰＰ
１　４　　　（イ）　　　　　　ａ＝ｍ∨（ａ＝ｎ∨ａ＝ｏ）　８結合法則
１　４　　　（ウ）　　　　　～ａ≠ｍ∨（ａ＝ｎ∨ａ＝ｏ）　イＤＮ
１　４　　　（エ）　　　　　　ａ≠ｍ→（ａ＝ｎ∨ａ＝ｏ）　ウ含意の定義
　　　　オ　（オ）　　　　　　ａ＝ｍ　　　　　　　　　　　Ａ
　　４　オ　（カ）　　　　　　　現場ｍ　　　　　　　　　　６オ＝Ｅ
１　４７オ　（キ）　　　　　　～現場ｍ＆現場ｍ　　　　　　７カ＆Ｅ
１　４７　　（ク）　　　　　　ａ≠ｍ　　　　　　　　　　　オキＲＡＡ
１　４７　　（ケ）　　　　　　　　　　（ａ＝ｎ∨ａ＝ｏ）　エクＭＰＰ
１　４７　　（コ）　　　　　　　　　　～ａ≠ｎ∨ａ＝ｏ　　ケＤＮ
１　４７　　（サ）　　　　　　　　　　　ａ≠ｎ→ａ＝ｏ　　コ含意の定義
　　　　　シ（シ）　　　　　　　　　　　ａ＝ｎ　　　　　　Ａ
　　４　　シ（ス）　　　　　　　現場ｎ　　　　　　　　　　６シ＝Ｅ
１　４７　シ（セ）　　　　　　～現場ｎ＆現場ｎ　　　　　　９ス＆Ｉ
１　４７　　（ソ）　　　　　　　　　　　ａ≠ｎ　　　　　　シセＲＡＡ
１　４７　　（タ）　　　　　　　　　　　　　　　ａ＝ｏ　　サソＭＰＰ
１　４７　　（チ）　　　犯人ｏ　　　　　　　　　　　　　　５タ
１２　７　　（ツ）　　　犯人ｏ　　　　　　　　　　　　　　２４チＥＥ
従って、
（08）により、
（09）
∀ｘ（犯人ｘ→ｘ＝ｍ∨ｘ＝ｎ∨ｘ＝ｏ），∃ｘ（犯人ｘ＆現場ｘ），～現場ｍ＆～現場ｎ├ 犯人ｏ
といふ「連式」、すなはち、
（ⅰ）∀ｘ（犯人ｘ→ｘ＝ｍ∨ｘ＝ｎ∨ｘ＝ｏ）。然るに、
（ⅱ）∃ｘ（犯人ｘ＆現場ｘ）。　　　　　　　　然るに、
（ⅲ）～現場ｍ＆～現場ｎ。　　　　　　　　　　従って、
（ⅳ）犯人ｏ。
といふ「推論」は「妥当」である。
従って、
（09）により、
（10）
（ⅰ）すべてのｘについて（ｘが犯人であるならば、ｘはｍか、ｘはｎか、ｏである。 然るに、
（ⅱ）　　あるｘについて（ｘは犯人であって、ｘは現場にゐた）。　　　　　　　　 然るに、
（ⅲ）ｍは現場にゐなかったし、ｎも現場にゐなかった。　　　　　　　　　　　　　 従って、
（ⅳ）ｏが犯人である（犯人はｏである）。
といふ「推論」は、「妥当」である。
従って、
（07）～（10）により、
（11）
（ⅰ）犯人は、森山か、中村か、太田である。然るに、
（ⅱ）犯人は、現場にゐた。　　　　　　　　然るに、
（ⅲ）森山と中村には、アリバイがある。　　従って、
（ⅳ）太田が犯人である（犯人は太田である）。
といふ「推論」は、「日本語」としても、「述語論理（Predicate logic）」としても「妥当」である。
令和０４年０７月１６日、毛利太。

「犯人は鈴木か渡辺である」の「述語論理」。

（01）
１　　　　（１）∀ｘ（犯人ｘ→ｘ＝ｓ∨ｘ＝ｋ）　Ａ
　２　　　（２）∃ｘ（犯人ｘ＆現場ｘ）　　　　　Ａ
１　　　　（３）　　　犯人ａ→ａ＝ｓ∨ａ＝ｋ　　１ＵＥ
　　４　　（４）　　　犯人ａ＆現場ａ　　　　　　Ａ
　　４　　（５）　　　犯人ａ　　　　　　　　　　４＆Ｅ
　　４　　（６）　　　　　　　現場ａ　　　　　　４＆Ｅ
　　　７　（７）　　　　　　～現場ｋ　　　　　　Ａ
１　４　　（８）　　　　　　　ａ＝ｓ∨ａ＝ｋ　　３５ＭＰＰ
１　４　　（９）　　　　　　　ａ＝ｋ∨ａ＝ｓ　　８交換法則
１　４　　（ア）　　　　　　～ａ≠ｋ∨ａ＝ｓ　　９ＤＮ
１　４　　（イ）　　　　　　　ａ≠ｋ→ａ＝ｓ　　ア含意の定義
　　　　ウ（ウ）　　　　　　　ａ＝ｋ　　　　　　Ａ
　　４　ウ（エ）　　　　　　　現場ｋ　　　　　　６ウ＝Ｅ
　　４７ウ（オ）　　　　　　～現場ｋ＆現場ｋ　　７エ＆Ｉ
　　４７　（カ）　　　　　　　ａ≠ｋ　　　　　　ウオＲＡＡ
１　４７　（キ）　　　　　　　　　　　ａ＝ｓ　　イカＭＰＰ
１　４７　（ク）　　　犯人ｓ　　　　　　　　　　５キ＝Ｅ
１２　７　（ケ）　　　犯人ｓ　　　　　　　　　　２４クＥＥ
従って、
（01）により、
（02）
∀ｘ（犯人ｘ→ｘ＝ｓ∨ｘ＝ｋ），∃ｘ（犯人ｘ＆現場ｘ），～現場ｋ├ 犯人ｓ
といふ「推論」は「妥当」である。
従って、
（02）により、
（03）
（ⅰ）∀ｘ（犯人ｘ→ｘ＝ｓ∨ｘ＝ｋ）。然るに、
（ⅱ）∃ｘ（犯人ｘ＆現場ｘ）。　　　　然るに、
（ⅲ）～現場ｋ。　　　　　　　　　　　従って、
（ⅳ）犯人ｓ。
といふ「推論」は「妥当」である。
従って、
（03）により、
（04）
（ⅰ）すべてのｘについて（ｘが犯人であるならば、ｘはｓか、または、ｘはｋである）。然るに、
（ⅱ）あるｘは（犯人であって、ｘは現場にゐた）。然るに、
（ⅲ）ｋは現場にはゐなかった。従って、
（ⅳ）ｓが犯人である（犯人はｓである）。
といふ「推論」は「妥当」である。
従って、
（01）～（04）により、
（05）
（ⅰ）犯人は、鈴木か、または、窪田である。　然るに、
（ⅱ）犯人は、現場にゐた。　　　　　　　　　然るに、
（ⅲ）窪田は、現場にゐなかった。　　　　　　従って、
（ⅳ）鈴木が犯人である（犯人は鈴木である）。
といふ「推論」は、「数学の論理学」である所の「述語論理（Predicate logic）」としても「妥当」である。
然るに、
（06）
鈴木は「個人（individual）」である。
従って、
（02）（06）により、
（07）
② 犯人は鈴木である。
③ 鈴木以外は犯人ではない。
に於いて、
②＝③ であるが、このことは、
① ∀ｘ（犯人ｘ→ｘ＝ｓ∨ｘ＝ｋ），∃ｘ（犯人ｘ＆現場ｘ），～現場ｋ├ 犯人ｓ
といふ「連式」の「意味」からすれば、「当然」である。
然るに、
（08）
よく知られているように、「私が理事長です」は語順を変え、
　理事長は、私です。 と直して初めて主辞賓辞が適用されるのである。また、かりに大倉氏が、
　タゴール記念会は、私が理事長です。
と言ったとすれば、これは主辞「タゴール記念会」を品評するという心持ちの文である。
（三上章、日本語の論理、1963年、４０・４１頁）
従って、
（08）により、
（09）
② 私が理事長です。
③ 理事長は私です。
に於いて、
②＝③ である。
然るに、
（10）
私は「個人（individual）」である。
従って、
（10）により、
（11）
② 理事長は私である。
③ 私以外は理事長ではない。
に於いて、
②＝③ である。
従って、
（05）～（11）により、
（12）
① 鈴木が犯人である。
② 犯人は鈴木である。
③ 鈴木以外は犯人ではない。
に於いて、
①＝②＝③ であって、
① 私が理事長である。
② 理事長は私である。
③ 私以外は理事長ではない。
に於いて、
①＝②＝③ である。
従って、
（12）により、
（13）
① ＡがＢである。
② ＢはＡである。
③ Ａ以外はＢでない。
に於いて、
①＝②＝③ である。
令和０４年０７月１５日、毛利太。

「強選言（排他的選言）」と「弱選言（包含的選言）」と「選言三段論法」（Ⅱ）。

（01）
日本語の接続詞「あるいは」には、両立的選言（弱選言）と排他的選言（強選言）の二つの意味があることに注意してほしい。

　― 中略 ―
排他的選言の方は∨と＆と～によって簡単に表現できる―（Ｐ∨Ｑ）＆～（Ｐ＆Ｑ）―。
選言記号∨に対応する日本語には、「または」「もしくは」「・・・か・・・」などがある。
（昭和堂入門選書２５、論理学の基礎、1994年、１１頁改）
従って、
（01）により、
（02）
①「排他的選言（強選言）」
②（Ｐ∨Ｑ）＆～（Ｐ＆Ｑ）
③（Ｐまたは、Ｑである）が、（ＰであってＱである）といふことはない。
に於いて、
①＝②＝③ である。
然るに、
（03）
（ⅰ）
１　　　（１）　　　Ｐ∨　Ｑ　　Ａ
　２　　（２）　　～Ｐ＆～Ｑ　　Ａ
　　３　（３）　　　Ｐ　　　　　Ａ
　２　　（４）　　～Ｐ　　　　　２＆Ｅ
　２３　（５）　　　Ｐ＆～Ｐ　　３４＆Ｉ
　　３　（６）～（～Ｐ＆～Ｑ）　２５ＲＡＡ
　　　７（７）　　　　　　Ｑ　　Ａ
　２　　（８）　　　　　～Ｑ　　２＆Ｅ
　２　７（９）　　　Ｑ＆～Ｑ　　７８＆Ｉ
　　　７（ア）～（～Ｐ＆～Ｑ）　２９ＲＡＡ
１　　　（イ）～（～Ｐ＆～Ｑ）　１３６７ア∨Ｅ
（ⅱ）
１　　　（１）～（～Ｐ＆～Ｑ）　　Ａ
　２　　（２）　～（Ｐ∨　Ｑ）　　Ａ
　　３　（３）　　　Ｐ　　　　　　Ａ
　　３　（４）　　　Ｐ∨　Ｑ　　　３∨Ｉ
　２３　（５）　～（Ｐ∨　Ｑ）＆
　　　　　　　　　（Ｐ∨　Ｑ）　　２４＆Ｉ
　２　　（６）　　～Ｐ　　　　　　３５ＲＡＡ
　　　７（７）　　　　　　Ｑ　　　Ａ
　　　７（８）　　　Ｐ∨　Ｑ　　　７∨Ｉ
　２　７（９）　～（Ｐ∨　Ｑ）＆
　　　　　　　　　（Ｐ∨　Ｑ）　　２８＆Ｉ
　２　　（ア）　　　　　～Ｑ　　　７９ＲＡＡ
　２　　（イ）　　～Ｐ＆～Ｑ　　　６ア＆Ｉ
１２　　（ウ）～（～Ｐ＆～Ｑ）＆
　　　　　　　　（～Ｐ＆～Ｑ）　　１イ＆Ｉ
１　　　（エ）～～（Ｐ∨　Ｑ）　　２ウＲＡＡ
１　　　（オ）　　　Ｐ∨　Ｑ　　　エＤＮ
従って、
（03）により、
（04）
①　　　 Ｐ∨　Ｑ
② ～（～Ｐ＆～Ｑ）
に於いて、
①＝② である（ド・モルガンの法則）。
従って、
（02）（03）（04）により、
（05）
①「排他的選言（強選言）」
②　　 （Ｐ∨  Ｑ）＆～（Ｐ＆Ｑ）
③ ～（～Ｐ＆～Ｑ）＆～（Ｐ＆Ｑ）
に於いて、
①＝②＝③ である。
従って、
（01）（05）により、
（06）
①　　 （Ｐ∨　Ｑ）
②　　 （Ｐ∨  Ｑ）＆～（Ｐ＆Ｑ）
③ ～（～Ｐ＆～Ｑ）＆～（Ｐ＆Ｑ）
に於いて、
① は「両立的選言（弱選言）」であって、
② は「排他的選言（強選言）」である。
③ も「排他的選言（強選言）」である。
然るに、
（07）
１　　　　（１）～（～Ｐ＆～Ｑ）＆～（Ｐ＆　Ｑ）　Ａ
１　　　　（２）～（～Ｐ＆～Ｑ）　　　　　　　　　１＆Ｅ
　３　　　（３）　　～Ｐ　　　　　　　　　　　　　Ａ
　　４　　（４）　　　　　～Ｑ　　　　　　　　　　Ａ
　３４　　（５）　　～Ｐ＆～Ｑ　　　　　　　　　　３４＆Ｉ
１３４　　（６）～（～Ｐ＆～Ｑ）＆（～Ｐ＆～Ｑ）　２５＆Ｉ
１３　　　（７）　　　　～～Ｑ　　　　　　　　　　４６ＲＡＡ
１３　　　（８）　　　　　　Ｑ　　　　　　　　　　７ＤＮ
１　　　　（９）　　～Ｐ→　Ｑ　　　　　　　　　　３８ＣＰ
１　　　　（ア）　　　　　　　　　～（Ｐ＆　Ｑ）　１＆Ｅ
　　　イ　（イ）　　　　　　　　　　　Ｐ　　　　　Ａ
　　　　ウ（ウ）　　　　　　　　　　　　　　Ｑ　　Ａ
　　　イウ（エ）　　　　　　　　　　　Ｐ＆　Ｑ　　アウ＆Ｉ
１　　イウ（オ）　　～（Ｐ＆　Ｑ）＆（Ｐ＆　Ｑ）　アエ＆Ｉ
１　　イ　（カ）　　　　　　　　　　　　　～Ｑ　　ウオＲＡＡ
１　　　　（キ）　　　　　　　　　　　Ｐ→～Ｑ　　イカＣＰ
１　　　　（ク）　　　（～Ｐ→Ｑ）＆（Ｐ→～Ｑ）　９キ＆Ｉ
従って、
（06）（07）により、
（08）
①　　 （Ｐ∨　Ｑ）
②　　 （Ｐ∨  Ｑ）＆～（Ｐ＆Ｑ）
③ ～（～Ｐ＆～Ｑ）＆～（Ｐ＆Ｑ）
に於いて、
① ├（～Ｐ→Ｑ）
② ├（～Ｐ→Ｑ）＆（Ｐ→～Ｑ）
③ ├（～Ｐ→Ｑ）＆（Ｐ→～Ｑ）
といふ「連式」は「妥当」である。
従って、
（06）（07）（08）により、
（09）
一般に自然言語では、論理和的な文がこれら2つのうちどちらの意味であるかは曖昧な場合が多いが、その違いは重要である。
Ｐであるか、またはＱである。
Ｐでない。
したがって、Ｑである。
この場合、「両立的」にも「排他的」にも解釈できる。しかし、次の場合は「排他的論理和」でのみ成り立つ。
Ｐであるか、またはＱである。
Ｐである。
したがって、Ｑでない。
「両立的論理和」と解釈すると、上記の帰結は導けない。これを『選言肯定の誤謬』という（ウィキペディア改）。
といふ「説明」は、「正しい」。
令和０４年０７月１４日、毛利太。

「強選言（排他的選言）」と「弱選言（包含的選言）」と「選言三段論法」。

（01）
選言三段論法は、「または」が「包含的; inclusive」であっても「排他的; exclusive」であっても機能することに注意されたい（詳しくは後述）。
（ウィキペディア）
（02）
日常的な言語では、「ＡまたはＢ」という言葉は、ＡとＢが両方真となる包含的論理和（inclusive disjunction, or）と、
いずれか一方が真でいずれか一方が偽となる排他的論理和（exclusive disjunction, xor）が区別されていないことがあります。
選言三段論法が妥当となるときは、後者、排他的論理和として「または」を使っているときに限られることがわかりますね。
（趣味の数学）
従って、
（01）（02）により、
（03）
①「選言三段論法」は「包含的; inclusive」であっても「排他的; exclusive」であっても機能する（ウィキペディア）。
②「選言三段論法」は「排他的論理和」として「または」を使っているときに限られることがわかりますね（趣味の数学）。
となってゐて、もちろん、①と② は、『矛盾』する。
然るに、
（04）
（ⅰ）犯人はＡかＢ（、または、両方）である。然るに、
（ⅱ）Ａは犯人ではない。　従って、
（ⅲ）Ｂが犯人である。
といふ「選言三段論法」は、明らかに、「妥当」である。
然るに、
（05）
（ⅰ）犯人はＡかＢ（のどちらか一方）である。然るに、
（ⅱ）Ａは犯人ではない。　従って、
（ⅲ）Ｂが犯人である。
といふ「選言三段論法」も、明らかに、「妥当」である。
然るに、
（02）により、
（06）
① 犯人はＡかＢ（、または、両方）である。
② 犯人はＡかＢ（のどちらか一方）である。
に於いて、
① は「弱選言（包含的選言）」である。
② は「強選言（排他的選言）」である。
従って、
（01）～（06）により、
（07）
①「選言三段論法」は「包含的; inclusive」であっても「排他的; exclusive」であっても機能する（ウィキペディア）。
②「選言三段論法」は「排他的論理和」として「または」を使っているときに限られることがわかりますね（趣味の数学）。
に於いて、
① が「正しく」、
② は「間違ひ」である。
然るに、
（02）により、
（08）
① Ｐか、または、Ｑであるか、または、両方である。
② ＰであってＱでないか、または、ＱであってＰでない。
に於いて、
① は、「弱選言（包含的選言）」であって、
② は、「強選言（排他的選言）」であるものの、以下では、
① Ｐ∨Ｑ
② Ｐ▽Ｑ
といふ風に、書くことにするが、「論理学の記号」として、
① は、「普通」であって、
② は、「特殊」である。
然るに、
（09）
① Ｐか、または、Ｑであるか、または、両方である。
② ＰであってＱでないか、または、ＱであってＰでない。
といふ「日本語」は、
①  Ｐ∨Ｑ
②（Ｐ＆～Ｑ）∨（Ｑ＆～Ｐ）
といふ風に、書くこと出来る。
然るに、
（10）
（ⅰ）
１　　　（１）　　Ｐ∨Ｑ　Ａ
　２　　（２）　　Ｐ　　　Ａ
　２　　（３）～～Ｐ　　　２ＤＮ
　２　　（４）～～Ｐ∨Ｑ　３∨Ｉ
　　５　（５）　　　　Ｑ　Ａ
　　５　（６）～～Ｐ∨Ｑ　５∨Ｉ
１　　　（７）～～Ｐ∨Ｑ　１２４５６∨Ｅ
１　　　（８）　～Ｐ→Ｑ　７含意の定義
　　　９（９）　～Ｐ　　　Ａ
１　　９（ア）　　　　Ｑ　８９ＭＰＰ
（ⅱ）
１　　　　　（１）　Ｐ▽　Ｑ　　　　　　　　　Ａ
１　　　　　（２）（Ｐ＆～Ｑ）∨（Ｑ＆～Ｐ）　１Ｄｆ.▽
　３　　　　（３）（Ｐ＆～Ｑ）　　　　　　　　Ａ
　３　　　　（４）　Ｐ　　　　　　　　　　　　３＆Ｅ
　３　　　　（５）　Ｐ∨Ｑ　　　　　　　　　　４∨Ｉ
　３　　　　（６）　　　～Ｑ　　　　　　　　　３＆Ｅ
　３　　　　（７）～Ｐ∨～Ｑ　　　　　　　　　６∨Ｉ
　３　　　　（８）～（Ｐ＆Ｑ）　　　　　　　　７ド・モルガンの法則
　３　　　　（９）　（Ｐ∨Ｑ）＆～（Ｐ＆Ｑ）　５８＆Ｉ
　　ア　　　（ア）　　　　　　　（Ｑ＆～Ｐ）　Ａ
　　ア　　　（イ）　　　　　　　　Ｑ　　　　　ア＆Ｅ
　　ア　　　（ウ）　　　　　　Ｐ∨Ｑ　　　　　イ∨Ｉ
　　ア　　　（エ）　　　　　　　　　　～Ｐ　　ア＆Ｅ
　　ア　　　（オ）　　　　　　　～Ｐ∨～Ｑ　　エ∨Ｉ
　　ア　　　（カ）　　　　　　　～（Ｐ＆Ｑ）　オ、ド・モルガンの法則
　　ア　　　（キ）　（Ｐ∨Ｑ）＆～（Ｐ＆Ｑ）　ウカ＆Ｉ
１　　　　　（ク）　（Ｐ∨Ｑ）＆～（Ｐ＆Ｑ）　２３９アキ∨Ｅ
１　　　　　（ケ）　　Ｐ∨Ｑ　　　　　　　　　Ａ
　　　コ　　（コ）　　Ｐ　　　　　　　　　　　Ａ
　　　コ　　（サ）～～Ｐ　　　　　　　　　　　コＤＮ
　　　コ　　（シ）～～Ｐ∨Ｑ　　　　　　　　　サ∨Ｉ
　　　　ス　（ス）　　　　Ｑ　　　　　　　　　Ａ
　　　　ス　（セ）～～Ｐ∨Ｑ　　　　　　　　　ス∨Ｉ
１　　　　　（ソ）～～Ｐ∨Ｑ　　　　　　　　　ケコシスセ∨Ｅ
１　　　　　（タ）　～Ｐ→Ｑ　　　　　　　　　ソ含意の定義
　　　　　チ（チ）　～Ｐ　　　　　　　　　　　Ａ
１　　　　チ（ツ）　　　　Ｑ　　　　　　　　　タチＭＰＰ
従って、
（10）により、
（11）
① Ｐ∨Ｑ，～Ｐ├ Ｑ
② Ｐ▽Ｑ，～Ｐ├ Ｑ
といふ「推論」は、両方とも「妥当」である。
従って、
（07）～（11）により、
（12）
①「弱選言（包含的選言）三段論法」と、
②「強選言（排他的選言）三段論法」は、
両方とも、「命題計算」として、「妥当」である。
従って、
（04）（05）（06）（12）により、
（13）
「日本語（日常言語）」としても、
「論理学（命題計算）」としても、
①「弱選言（包含的選言）三段論法」と、
②「強選言（排他的選言）三段論法」は、
両方とも、「妥当」である。
従って、
（02）（13）により、
（14）
日常的な言語では、「ＡまたはＢ」という言葉は、ＡとＢが両方真となる包含的論理和（inclusive disjunction, or）と、
いずれか一方が真でいずれか一方が偽となる排他的論理和（exclusive disjunction, xor）が区別されていないことがあります。
選言三段論法が妥当となるときは、後者、排他的論理和として「または」を使っているときに限られることがわかりますね。
といふ『誤解』は、
「日本語（日常言語）」としても、
「論理学（命題計算）」としても、『誤解』である。
然るに、
（15）
１　　（１）　Ｐ▽　Ｑ　　　　　　　　　Ａ
１　　（２）（Ｐ＆～Ｑ）∨（Ｑ＆～Ｐ）　１Ｄｆ.▽
　３　（３）　Ｐ＆～Ｑ　　　　　　　　　Ａ
　３　（４）　Ｐ　　　　　　　　　　　　３＆Ｅ
　３　（５）　Ｐ∨Ｑ　　　　　　　　　　４∨Ｉ
　　６（６）　　　　　　　　Ｑ＆～Ｐ　　Ａ
　　６（７）　　　　　　　　Ｑ　　　　　５＆Ｅ
　　６（８）　　　　　　　　Ｐ∨Ｑ　　　７∨Ｉ
１　　（９）　Ｐ∨Ｑ　　　　　　　　　　１３５６８∨Ｅ
従って、
（15）により、
（16）
③ Ｐ▽Ｑ├ Ｐ∨Ｑ
といふ「推論」は「妥当」である。
従って、
（11）（16）により、
（17）
① 　　　　 Ｐ∨Ｑ，～Ｐ├ Ｑ
② Ｐ▽Ｑ├ Ｐ∨Ｑ，～Ｐ├ Ｑ
といふ「推論」は「妥当」である。
すなはち、
（18）
「強選言（排他的選言）」は、
「弱選言（包含的選言）」を、「含意」する。
令和０４年０７月１４日、毛利太。